京改版数学九年级上册 22.2 圆的切线 课件(27PPT共2课时)
文档属性
| 名称 | 京改版数学九年级上册 22.2 圆的切线 课件(27PPT共2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 419.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 14:40:26 | ||
图片预览





文档简介
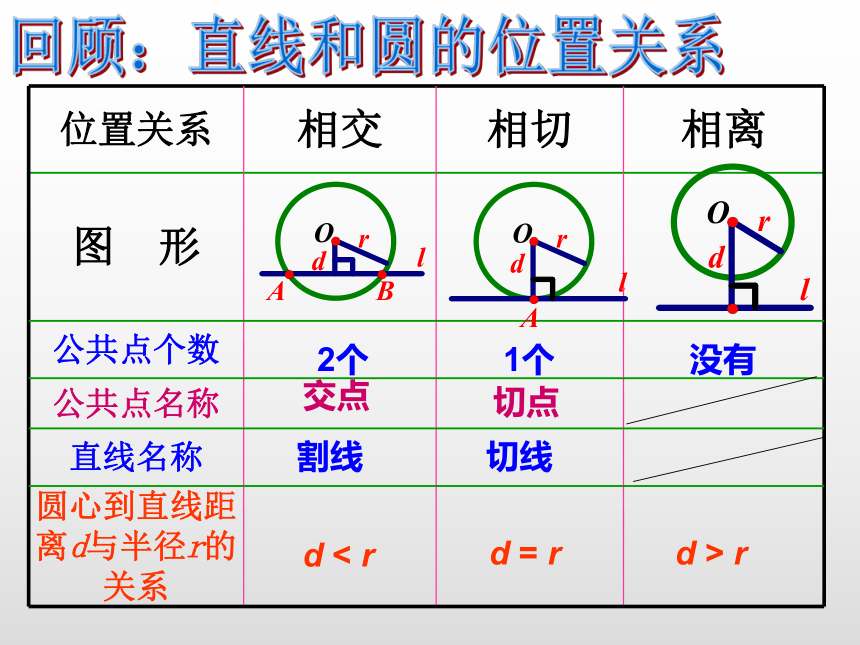
课件27张PPT。圆的切线第一课时2个交点割线1个切点切线d < rd = rd > r没有回顾:直线和圆的位置关系 下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞出的火星,均沿着圆的切线的方向飞出.1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨零件飞出火星的方向是什么方向?情景导入经过半径的外端且垂于这条半径
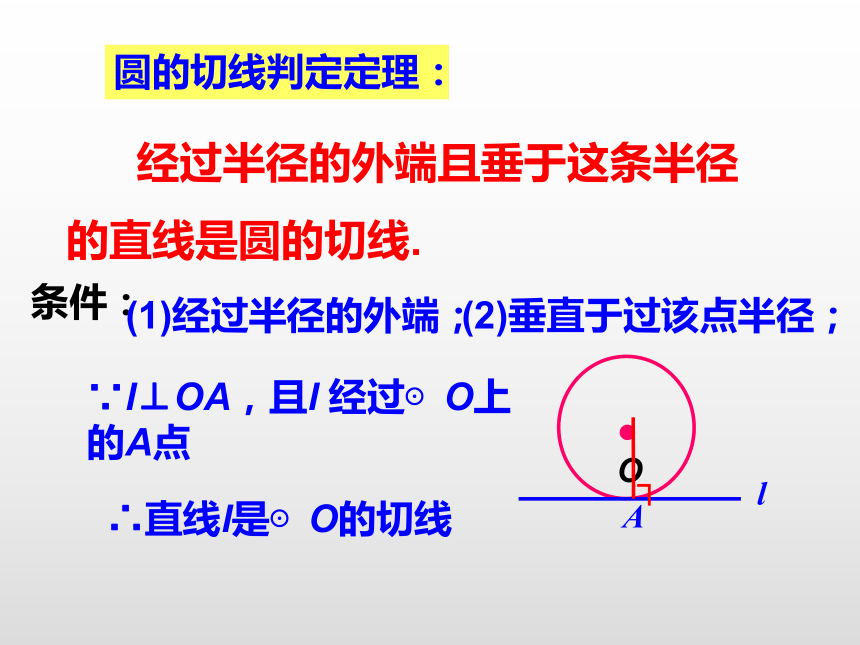
的直线是圆的切线. 条件:(1)经过半径的外端;圆的切线判定定理:(2)垂直于过该点半径;┐Al∵l⊥OA,且l 经过⊙O上 的A点∴直线l是⊙O的切线.OAL思考 如图:如果直线L是⊙O的切线,切点为A,那么半径OA与直线L是不是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径∵直线L是⊙O的切线,A是切点. ∴L⊥OA于A点简记为:“知切线,连半径,得垂直”切线的性质定理的应用已知Rt△ABC的斜边AB=8cm,直角边
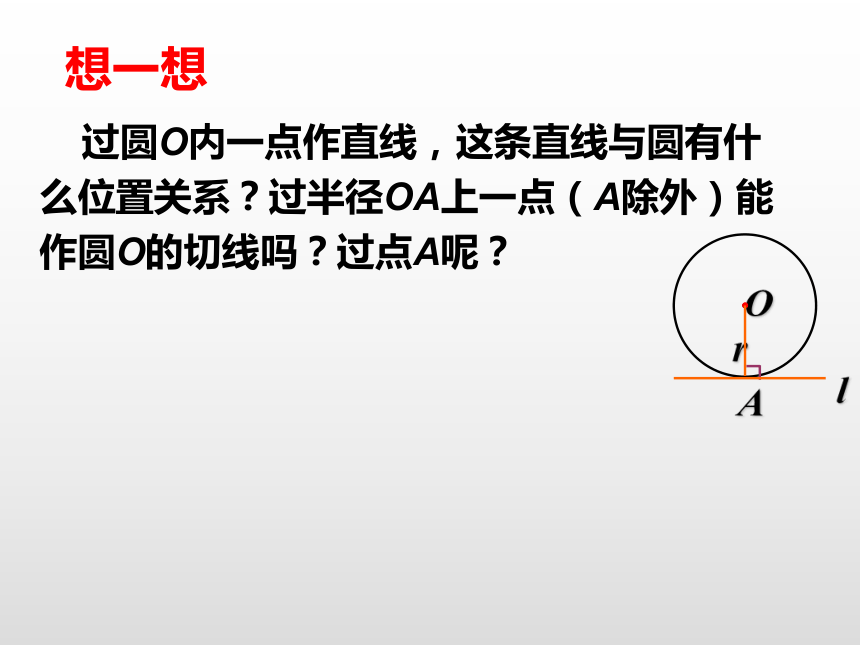
AC=4cm.以点C为圆心作圆,当半径为多长时,AB与⊙C相切.解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.∴∠A=60°因此,当半径长为 cm时,AB与⊙C相切.B∴∠B=30°想一想 过圆O内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?Orl A判 断1. 过半径的外端的直线是圆的切线( )
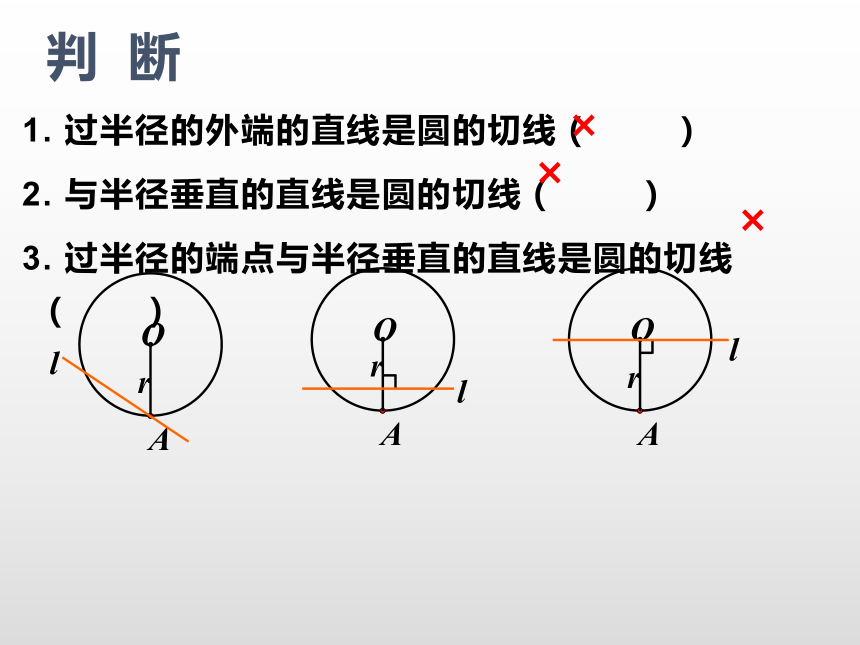
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××1、如何判定一条直线是已知圆的切线?(1)与圆只有一个公共点的直线是圆的切线;(2)到圆心的距离等于半径的直线是圆的
切线;(3)过半径外端点且和半径垂直的直线
是圆的切线;(d=r)归纳:直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,OC
是底边AB上的中线∴OC⊥AB∴AB是⊙O的切线OCBA这种证明方法简记为:“证切线,连半径,证垂垂直”注意:使用此方法时必须已知直线与圆有一公共点解:直线AC与⊙O相切.
理由如下:例1 已知:如图22-6,AB为⊙O的直径,AB=1cm,BC= cm,AC=1cm.判断直线AC与⊙O是否相切,并说明理由.∵AB=1,BC= ,AC=1,∴AB2+AC2=BC2.∴△ABC为直角三角形,∠BAC=900.∵AB为⊙O的直径,∴直线AC经过⊙O半径的外端A.∴直线AC与⊙O相切,A为切点.例2 如图所示,AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数.解:连接OA∵ AB是⊙O的弦∴ OA⊥AC即∠OAC=90°∴∠OAB=90°-∠CAB=46°又∵OA=OB∴∠OBA=∠OAB=46°练习1 如图,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么? BACO解:∵AB=AC ∴∠ACB=∠ABC=45° ∴∠BAC=90° 即AB⊥AC ∵ AB是⊙O的直径 ∴ AC是⊙O的切线变式练习练习2 如图:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D.BD是⊙O的切线吗?为什么? AOBCD解:BD是⊙O的切线连接OD ∵ OD=OA ∴∠ODA=∠BAD=∠B=30° ∴∠ BOD=60° ∴∠ODB=90° 即: OD⊥DB ∴BD是⊙O的切线变式练习已知:P为⊙O外一点,以OP为直径作圆交⊙O于A、B两点,连接PA、PB
那么PA、PB是⊙O的切线吗?AB1.切线和圆只有一个公共点.2.切线和圆心的距离等于半径.3.切线垂直于过切点的半径.4.经过圆心垂直于切线的直线必过切点.5.经过切点垂直于切线的直线必过圆心.切线的性质:切线的性质可归纳为:已知直线满足a.过圆心,b.过切点,c.垂直于切线中任意两个,便得到第三个结论.总结:第二课时切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.过圆外一点所画的圆的两条切线长相等. 几何语言:三角形内切圆内切圆圆心:三角形三个内角平分线的交点
内切圆的半径:交点到三角形任意一边的垂直距离ABC这个三角形称为这个圆的外切三角形.内切圆圆心叫做三角形的内心.例3 如图 ,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.解:连接 OD,OE,OF,设 OD = r.
在 Rt△ABC 中,AC = 10,BC = 24,
∵ ⊙O 分别与 AB,BC,CA 相切于点 D,E,F,∴ OD⊥AB,OE⊥BC,OF⊥AC,BE =BD,
AF =AD, CE =CF.
又∵ ∠C = 90° ,∴ 四边形OECF 为正方形.
∴EC = FC = r. BE = 24 –r,AF = 10 - r.
∴AB =BD + AD = BE + AF = 34 - 2r = 26.
∴ r = 4,
即 ⊙O半径为4.例4 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x,则AE=x∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.由BD+CD=BC可得
13-x+9-x=14,解得x=4.∴ AF=4 cm, BD=5 cm, CE=9 cm.已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=5cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=5cm,PF+FQ=PB=PA=5cm.∴周长为10cm.F再 见
2.砂轮打磨零件飞出火星的方向是什么方向?情景导入经过半径的外端且垂于这条半径
的直线是圆的切线. 条件:(1)经过半径的外端;圆的切线判定定理:(2)垂直于过该点半径;┐Al∵l⊥OA,且l 经过⊙O上 的A点∴直线l是⊙O的切线.OAL思考 如图:如果直线L是⊙O的切线,切点为A,那么半径OA与直线L是不是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径∵直线L是⊙O的切线,A是切点. ∴L⊥OA于A点简记为:“知切线,连半径,得垂直”切线的性质定理的应用已知Rt△ABC的斜边AB=8cm,直角边
AC=4cm.以点C为圆心作圆,当半径为多长时,AB与⊙C相切.解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.∴∠A=60°因此,当半径长为 cm时,AB与⊙C相切.B∴∠B=30°想一想 过圆O内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?Orl A判 断1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××1、如何判定一条直线是已知圆的切线?(1)与圆只有一个公共点的直线是圆的切线;(2)到圆心的距离等于半径的直线是圆的
切线;(3)过半径外端点且和半径垂直的直线
是圆的切线;(d=r)归纳:直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,OC
是底边AB上的中线∴OC⊥AB∴AB是⊙O的切线OCBA这种证明方法简记为:“证切线,连半径,证垂垂直”注意:使用此方法时必须已知直线与圆有一公共点解:直线AC与⊙O相切.
理由如下:例1 已知:如图22-6,AB为⊙O的直径,AB=1cm,BC= cm,AC=1cm.判断直线AC与⊙O是否相切,并说明理由.∵AB=1,BC= ,AC=1,∴AB2+AC2=BC2.∴△ABC为直角三角形,∠BAC=900.∵AB为⊙O的直径,∴直线AC经过⊙O半径的外端A.∴直线AC与⊙O相切,A为切点.例2 如图所示,AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数.解:连接OA∵ AB是⊙O的弦∴ OA⊥AC即∠OAC=90°∴∠OAB=90°-∠CAB=46°又∵OA=OB∴∠OBA=∠OAB=46°练习1 如图,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么? BACO解:∵AB=AC ∴∠ACB=∠ABC=45° ∴∠BAC=90° 即AB⊥AC ∵ AB是⊙O的直径 ∴ AC是⊙O的切线变式练习练习2 如图:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D.BD是⊙O的切线吗?为什么? AOBCD解:BD是⊙O的切线连接OD ∵ OD=OA ∴∠ODA=∠BAD=∠B=30° ∴∠ BOD=60° ∴∠ODB=90° 即: OD⊥DB ∴BD是⊙O的切线变式练习已知:P为⊙O外一点,以OP为直径作圆交⊙O于A、B两点,连接PA、PB
那么PA、PB是⊙O的切线吗?AB1.切线和圆只有一个公共点.2.切线和圆心的距离等于半径.3.切线垂直于过切点的半径.4.经过圆心垂直于切线的直线必过切点.5.经过切点垂直于切线的直线必过圆心.切线的性质:切线的性质可归纳为:已知直线满足a.过圆心,b.过切点,c.垂直于切线中任意两个,便得到第三个结论.总结:第二课时切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.过圆外一点所画的圆的两条切线长相等. 几何语言:三角形内切圆内切圆圆心:三角形三个内角平分线的交点
内切圆的半径:交点到三角形任意一边的垂直距离ABC这个三角形称为这个圆的外切三角形.内切圆圆心叫做三角形的内心.例3 如图 ,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.解:连接 OD,OE,OF,设 OD = r.
在 Rt△ABC 中,AC = 10,BC = 24,
∵ ⊙O 分别与 AB,BC,CA 相切于点 D,E,F,∴ OD⊥AB,OE⊥BC,OF⊥AC,BE =BD,
AF =AD, CE =CF.
又∵ ∠C = 90° ,∴ 四边形OECF 为正方形.
∴EC = FC = r. BE = 24 –r,AF = 10 - r.
∴AB =BD + AD = BE + AF = 34 - 2r = 26.
∴ r = 4,
即 ⊙O半径为4.例4 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x,则AE=x∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.由BD+CD=BC可得
13-x+9-x=14,解得x=4.∴ AF=4 cm, BD=5 cm, CE=9 cm.已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=5cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=5cm,PF+FQ=PB=PA=5cm.∴周长为10cm.F再 见
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
