五年级上册数学 4.12 平行四边形的面积 教案 浙教版
文档属性
| 名称 | 五年级上册数学 4.12 平行四边形的面积 教案 浙教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 238.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 00:00:00 | ||
图片预览

文档简介
课题
平行四边形的面积
教学背景分析
教材简析:《平行四边形的面积计算》是按由易到难的顺序贯穿始终的。平行四边形面积的计算,是在学生已掌握了长方形面积的计算、面积概念和面积单位,以及认识了平行四边形的基础上进行教学的。教材运用转化思想,在数方格法的基础上,用割补法,把平行四边形转化成长方形,并分析长方形面积与平行四边形面积的关系,再从长方形的面积计算公式推出平行四边形的面积计算公式,然后通过实例验证,使学生理解平行四边形面积计算公式的推导过程,在理解的基础上掌握公式。本节课是长方形面积计算公式的延伸和后面学习三角形面积以及梯形面积计算的依据,因此这节课的内容在整个教材体系中起到承上启下的作用,也是整个单元学习的重点。
学生情况:五年级的学生已经掌握了平行四边形的特征和长方形、正方形面积的计算方法。这些都为本节课的学习奠定了坚实的知识基础,但他们主动性还比较欠缺,课堂精神容易分散,空间想象力不够丰富,对平行四边形面积计算公式的推导有一定的困难。因此本节课的学习结合他们这个年龄阶段好奇心强,喜欢参与动手活动的特点,让学生充分利用好已有知识,参与动手操作,更好的理解平行四方形面积的计算。
我的思考:
本节课充分运用转化迁移思想,重视学生动手操作与实践,引导学生用已学过的知识去获取新知。设计时,我力求做到以下几点:
1从学生已有的认知出发,体现教学的有效性
在复习长方形的面积的基础上,本课一开始让学生猜测平行四边形的面积大小跟什么有关,从而暴露学生的原认知,让学生通过讨论、交流产生思维的碰撞,逐步得到正确求平行四边形面积的方法。
2体现“教师是教材的创造者,学生是学习主体”的教学理念
本节课为学生提供广阔的时间和空间,让学生去发现,去探索、去创造,让学生在动手做中建构、内化、提升。
3有机渗透数学思想方法,培养学生能力
我们知道课堂上不仅仅是传授知识或者教会什么,而是让学生会学。本节课重在引导学生明白求平行四边形面积可以把它转化为长方形,根据长方形面积的计算方法求平行四边形的面积。另外通过学生动手剪拼,电脑演示,进一步渗透转化的思想方法。
教学手段:学生自主探究合作交流,教师引导学生完成学习任务。
技术准备:教学课件、方格纸、剪刀、平行四边形、平行四边形框架。
教学目标(内容框架)
1、掌握平行四边形的面积计算公式,会计算平行四边形的面积。培养学生的观察、操作、想象、推理、表达能力及解决实际问题的能力。
2、通过观察、操作、比较,经历探究平行四边形的面积计算方法的推导过程,渗透转化的思想,发展学生的空间观念。
3、在学习过程中使学生体会到运用旧知识解决新问题的乐趣,体会数学知识间的紧密联系。
教学重点:掌握平行四边形的面积计算公式,并能正确运用。
教学难点:理解平行四边形面积计算公式的推导过程。
教学过程
教学
环节
教师活动
学生活动
设计意图
一、
创
设
情
境
,
导
入
新
知
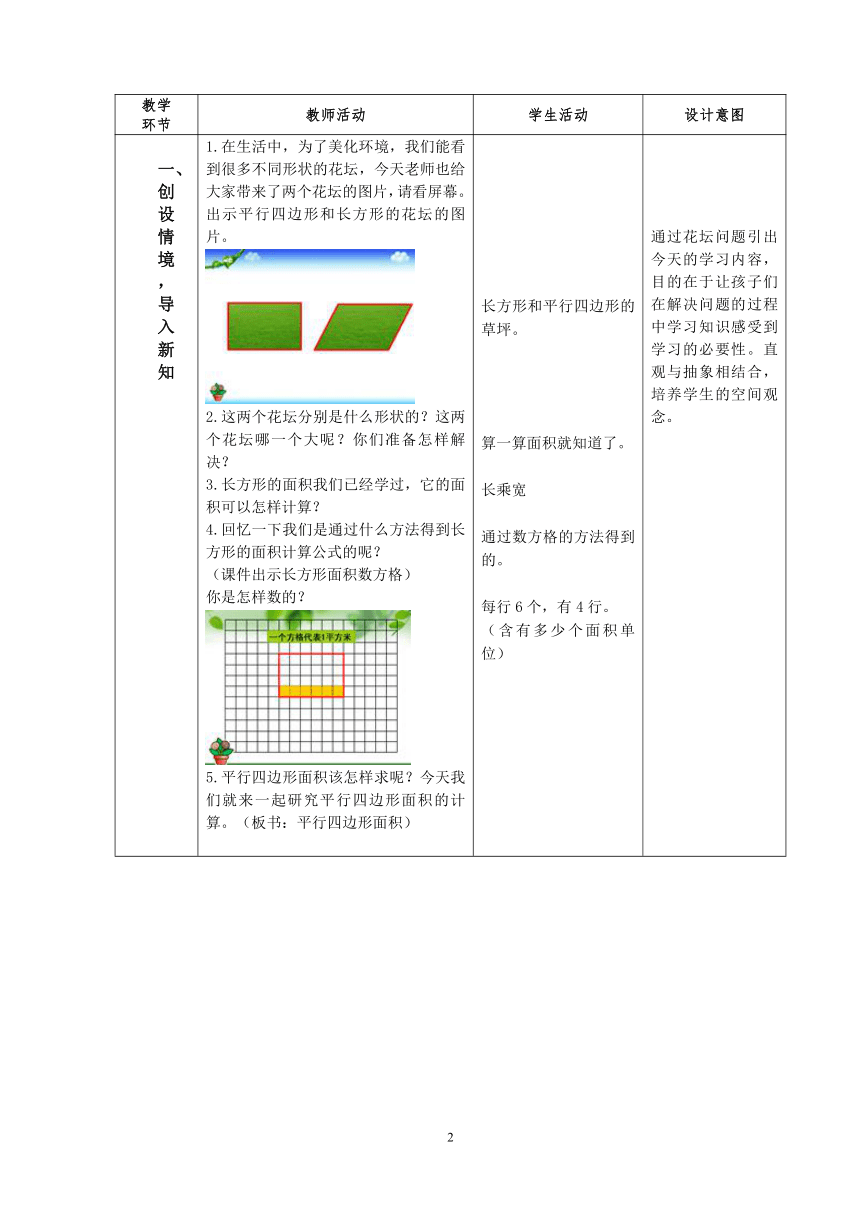
1.在生活中,为了美化环境,我们能看到很多不同形状的花坛,今天老师也给大家带来了两个花坛的图片,请看屏幕。出示平行四边形和长方形的花坛的图片。
2.这两个花坛分别是什么形状的?这两个花坛哪一个大呢?你们准备怎样解决?
3.长方形的面积我们已经学过,它的面积可以怎样计算?
4.回忆一下我们是通过什么方法得到长方形的面积计算公式的呢?
(课件出示长方形面积数方格)
你是怎样数的?
5.平行四边形面积该怎样求呢?今天我们就来一起研究平行四边形面积的计算。(板书:平行四边形面积)
长方形和平行四边形的草坪。
算一算面积就知道了。
长乘宽
通过数方格的方法得到的。
每行6个,有4行。
(含有多少个面积单位)
通过花坛问题引出今天的学习内容,目的在于让孩子们在解决问题的过程中学习知识感受到学习的必要性。直观与抽象相结合,培养学生的空间观念。
二、
实
践
操
作
,
探
索
新
知
三、
运
用
所
学
,
解
决
问
题
1.根据以前的经验猜一猜:平行四边形的面积怎样计算?
生1:底乘高
生2:邻边相乘
2.动手操作,验证猜想。
(1)小组合作,利用学具研究平行四边形面积的计算方法。
(2)想一想,为什么平行四边形的面积可以这样计算。
(3)在汇报时请向大家说明。
3.学生汇报
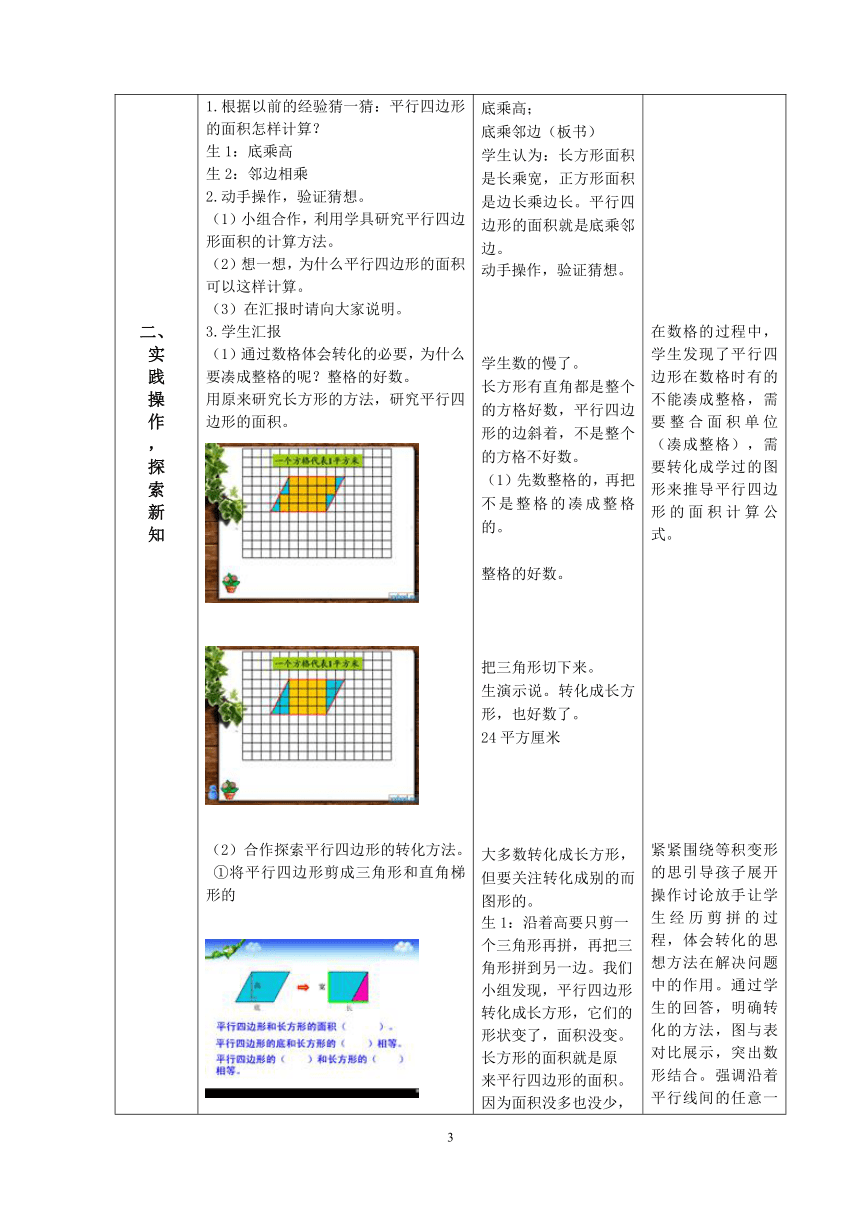
(1)通过数格体会转化的必要,为什么要凑成整格的呢?整格的好数。
用原来研究长方形的方法,研究平行四边形的面积。
(2)合作探索平行四边形的转化方法。
①将平行四边形剪成三角形和直角梯形的
将平行四边形转化成长方形之后,什么变了?什么没变?形状变了,但面积没变,所以求出长方形的面积也就是求出了平行四边形的面积。
它们之间有什么联系呢?
长方形的长相当于平行四边形的底,宽相当于平行四边形的高。从而推导出平行四边形面积等于底乘高。
②将平行四边形剪成两个直角梯形
面积变了吗?
长方形的长相当于平行四边形的底,宽相当于平行四边形的高,所以平行四边形的面积等于底乘高。
思考:这两种转化的方法有什么相同的地方吗?都是把平行四边形转化成长方形了。
沿这条高可以吗?这条呢?
为什么?
回顾平行四边形的转化过程,加深学生印象。
(6)用模型验证的
底乘邻边为什么不对呢?什么在变?面积在变,底和邻边变了吗?由此可以证明什么?平行四边形的面积不等于底乘邻边。
师操作:面积变小和什么有关系?高在变短,所以面积在变小......
4. 平行四边形面积的计算方法是什么?
5.用字母表示平行四边形的面积。
师板书规范格式:
S=ah
底乘高;
底乘邻边(板书)
学生认为:长方形面积是长乘宽,正方形面积是边长乘边长。平行四边形的面积就是底乘邻边。
动手操作,验证猜想。
学生数的慢了。
长方形有直角都是整个的方格好数,平行四边形的边斜着,不是整个的方格不好数。
(1)先数整格的,再把不是整格的凑成整格的。
整格的好数。
把三角形切下来。
生演示说。转化成长方形,也好数了。
24平方厘米
大多数转化成长方形,但要关注转化成别的而图形的。
生1:沿着高要只剪一
个三角形再拼,再把三
角形拼到另一边。我们
小组发现,平行四边形
转化成长方形,它们的
形状变了,面积没变。
长方形的面积就是原
来平行四边形的面积。
因为面积没多也没少,
只是形状变了。
平行四边形的底相当
于长方形的长,平行四
边形的高相当于长方
形的宽。
长方形的面积计算是:
长乘宽,由此,我们推
断出平行四边形的面
积就是底乘高。
生2:沿着一条高,剪
成两个直角梯形,再拼
成一个长方形。(说关
系)
1、都是把平行四边形转化成长方形了。(板书)
因为长方形的面积学过,转化成长方形面积就转化为旧知识了。很好解决了。
2、都是沿着高将平行四边形分割的。
因为长方形四个角都是直角,沿着平行四边形的高分割能得到直角,就能把平行四边形转化成长方形。
沿着哪条高都可以。
平行四边形有无数条高,所以哪条都可以。
底和邻边都没变,但高变短了所以面积变小了。
学生小组合作探究。
在数格的过程中,学生发现了平行四边形在数格时有的不能凑成整格,需要整合面积单位(凑成整格),需要转化成学过的图形来推导平行四边形的面积计算公式。
紧紧围绕等积变形的思引导孩子展开操作讨论放手让学生经历剪拼的过程,体会转化的思想方法在解决问题中的作用。通过学生的回答,明确转化的方法,图与表对比展示,突出数形结合。强调沿着平行线间的任意一条高剪开都可以。
再次证明平行四边形的面积等于底乘高,而不是邻边相乘。
1.
2.
3.
通过解答这道题,你发现了什么?
沿着15厘米长的底上的高剪开,面积应是15乘8;沿着9厘米长的底上的高剪开,面积应是9乘10。
4.
计算长方形和平行四边形花坛的面积,比较大小。
求平行四边形面积时一定要找准相对应的底和高。
已知面积和底求高。(面积公式逆用)
在求平行四边形面积时要找相对应的底和高。通过基本练习,帮助学生巩固所学。
四、
归
纳
总
结
,
引
出
新
知
通过归纳概括引导孩子们一步归纳、提升。为下面学习三角形和梯形面积打下基础。
方法:转化
注重知识之间的联系,为学生学习三角形和梯形面积做好孕伏。
平行四边形的面积
长方形面积= 长 × 宽
转化
平行四边形面积= 底 × 高
S = a h
平行四边形的面积
教学背景分析
教材简析:《平行四边形的面积计算》是按由易到难的顺序贯穿始终的。平行四边形面积的计算,是在学生已掌握了长方形面积的计算、面积概念和面积单位,以及认识了平行四边形的基础上进行教学的。教材运用转化思想,在数方格法的基础上,用割补法,把平行四边形转化成长方形,并分析长方形面积与平行四边形面积的关系,再从长方形的面积计算公式推出平行四边形的面积计算公式,然后通过实例验证,使学生理解平行四边形面积计算公式的推导过程,在理解的基础上掌握公式。本节课是长方形面积计算公式的延伸和后面学习三角形面积以及梯形面积计算的依据,因此这节课的内容在整个教材体系中起到承上启下的作用,也是整个单元学习的重点。
学生情况:五年级的学生已经掌握了平行四边形的特征和长方形、正方形面积的计算方法。这些都为本节课的学习奠定了坚实的知识基础,但他们主动性还比较欠缺,课堂精神容易分散,空间想象力不够丰富,对平行四边形面积计算公式的推导有一定的困难。因此本节课的学习结合他们这个年龄阶段好奇心强,喜欢参与动手活动的特点,让学生充分利用好已有知识,参与动手操作,更好的理解平行四方形面积的计算。
我的思考:
本节课充分运用转化迁移思想,重视学生动手操作与实践,引导学生用已学过的知识去获取新知。设计时,我力求做到以下几点:
1从学生已有的认知出发,体现教学的有效性
在复习长方形的面积的基础上,本课一开始让学生猜测平行四边形的面积大小跟什么有关,从而暴露学生的原认知,让学生通过讨论、交流产生思维的碰撞,逐步得到正确求平行四边形面积的方法。
2体现“教师是教材的创造者,学生是学习主体”的教学理念
本节课为学生提供广阔的时间和空间,让学生去发现,去探索、去创造,让学生在动手做中建构、内化、提升。
3有机渗透数学思想方法,培养学生能力
我们知道课堂上不仅仅是传授知识或者教会什么,而是让学生会学。本节课重在引导学生明白求平行四边形面积可以把它转化为长方形,根据长方形面积的计算方法求平行四边形的面积。另外通过学生动手剪拼,电脑演示,进一步渗透转化的思想方法。
教学手段:学生自主探究合作交流,教师引导学生完成学习任务。
技术准备:教学课件、方格纸、剪刀、平行四边形、平行四边形框架。
教学目标(内容框架)
1、掌握平行四边形的面积计算公式,会计算平行四边形的面积。培养学生的观察、操作、想象、推理、表达能力及解决实际问题的能力。
2、通过观察、操作、比较,经历探究平行四边形的面积计算方法的推导过程,渗透转化的思想,发展学生的空间观念。
3、在学习过程中使学生体会到运用旧知识解决新问题的乐趣,体会数学知识间的紧密联系。
教学重点:掌握平行四边形的面积计算公式,并能正确运用。
教学难点:理解平行四边形面积计算公式的推导过程。
教学过程
教学
环节
教师活动
学生活动
设计意图
一、
创
设
情
境
,
导
入
新
知
1.在生活中,为了美化环境,我们能看到很多不同形状的花坛,今天老师也给大家带来了两个花坛的图片,请看屏幕。出示平行四边形和长方形的花坛的图片。
2.这两个花坛分别是什么形状的?这两个花坛哪一个大呢?你们准备怎样解决?
3.长方形的面积我们已经学过,它的面积可以怎样计算?
4.回忆一下我们是通过什么方法得到长方形的面积计算公式的呢?
(课件出示长方形面积数方格)
你是怎样数的?
5.平行四边形面积该怎样求呢?今天我们就来一起研究平行四边形面积的计算。(板书:平行四边形面积)
长方形和平行四边形的草坪。
算一算面积就知道了。
长乘宽
通过数方格的方法得到的。
每行6个,有4行。
(含有多少个面积单位)
通过花坛问题引出今天的学习内容,目的在于让孩子们在解决问题的过程中学习知识感受到学习的必要性。直观与抽象相结合,培养学生的空间观念。
二、
实
践
操
作
,
探
索
新
知
三、
运
用
所
学
,
解
决
问
题
1.根据以前的经验猜一猜:平行四边形的面积怎样计算?
生1:底乘高
生2:邻边相乘
2.动手操作,验证猜想。
(1)小组合作,利用学具研究平行四边形面积的计算方法。
(2)想一想,为什么平行四边形的面积可以这样计算。
(3)在汇报时请向大家说明。
3.学生汇报
(1)通过数格体会转化的必要,为什么要凑成整格的呢?整格的好数。
用原来研究长方形的方法,研究平行四边形的面积。
(2)合作探索平行四边形的转化方法。
①将平行四边形剪成三角形和直角梯形的
将平行四边形转化成长方形之后,什么变了?什么没变?形状变了,但面积没变,所以求出长方形的面积也就是求出了平行四边形的面积。
它们之间有什么联系呢?
长方形的长相当于平行四边形的底,宽相当于平行四边形的高。从而推导出平行四边形面积等于底乘高。
②将平行四边形剪成两个直角梯形
面积变了吗?
长方形的长相当于平行四边形的底,宽相当于平行四边形的高,所以平行四边形的面积等于底乘高。
思考:这两种转化的方法有什么相同的地方吗?都是把平行四边形转化成长方形了。
沿这条高可以吗?这条呢?
为什么?
回顾平行四边形的转化过程,加深学生印象。
(6)用模型验证的
底乘邻边为什么不对呢?什么在变?面积在变,底和邻边变了吗?由此可以证明什么?平行四边形的面积不等于底乘邻边。
师操作:面积变小和什么有关系?高在变短,所以面积在变小......
4. 平行四边形面积的计算方法是什么?
5.用字母表示平行四边形的面积。
师板书规范格式:
S=ah
底乘高;
底乘邻边(板书)
学生认为:长方形面积是长乘宽,正方形面积是边长乘边长。平行四边形的面积就是底乘邻边。
动手操作,验证猜想。
学生数的慢了。
长方形有直角都是整个的方格好数,平行四边形的边斜着,不是整个的方格不好数。
(1)先数整格的,再把不是整格的凑成整格的。
整格的好数。
把三角形切下来。
生演示说。转化成长方形,也好数了。
24平方厘米
大多数转化成长方形,但要关注转化成别的而图形的。
生1:沿着高要只剪一
个三角形再拼,再把三
角形拼到另一边。我们
小组发现,平行四边形
转化成长方形,它们的
形状变了,面积没变。
长方形的面积就是原
来平行四边形的面积。
因为面积没多也没少,
只是形状变了。
平行四边形的底相当
于长方形的长,平行四
边形的高相当于长方
形的宽。
长方形的面积计算是:
长乘宽,由此,我们推
断出平行四边形的面
积就是底乘高。
生2:沿着一条高,剪
成两个直角梯形,再拼
成一个长方形。(说关
系)
1、都是把平行四边形转化成长方形了。(板书)
因为长方形的面积学过,转化成长方形面积就转化为旧知识了。很好解决了。
2、都是沿着高将平行四边形分割的。
因为长方形四个角都是直角,沿着平行四边形的高分割能得到直角,就能把平行四边形转化成长方形。
沿着哪条高都可以。
平行四边形有无数条高,所以哪条都可以。
底和邻边都没变,但高变短了所以面积变小了。
学生小组合作探究。
在数格的过程中,学生发现了平行四边形在数格时有的不能凑成整格,需要整合面积单位(凑成整格),需要转化成学过的图形来推导平行四边形的面积计算公式。
紧紧围绕等积变形的思引导孩子展开操作讨论放手让学生经历剪拼的过程,体会转化的思想方法在解决问题中的作用。通过学生的回答,明确转化的方法,图与表对比展示,突出数形结合。强调沿着平行线间的任意一条高剪开都可以。
再次证明平行四边形的面积等于底乘高,而不是邻边相乘。
1.
2.
3.
通过解答这道题,你发现了什么?
沿着15厘米长的底上的高剪开,面积应是15乘8;沿着9厘米长的底上的高剪开,面积应是9乘10。
4.
计算长方形和平行四边形花坛的面积,比较大小。
求平行四边形面积时一定要找准相对应的底和高。
已知面积和底求高。(面积公式逆用)
在求平行四边形面积时要找相对应的底和高。通过基本练习,帮助学生巩固所学。
四、
归
纳
总
结
,
引
出
新
知
通过归纳概括引导孩子们一步归纳、提升。为下面学习三角形和梯形面积打下基础。
方法:转化
注重知识之间的联系,为学生学习三角形和梯形面积做好孕伏。
平行四边形的面积
长方形面积= 长 × 宽
转化
平行四边形面积= 底 × 高
S = a h
同课章节目录
