第二章 基本初等函数(Ⅰ)(指对幂综合) 学案
文档属性
| 名称 | 第二章 基本初等函数(Ⅰ)(指对幂综合) 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 08:56:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
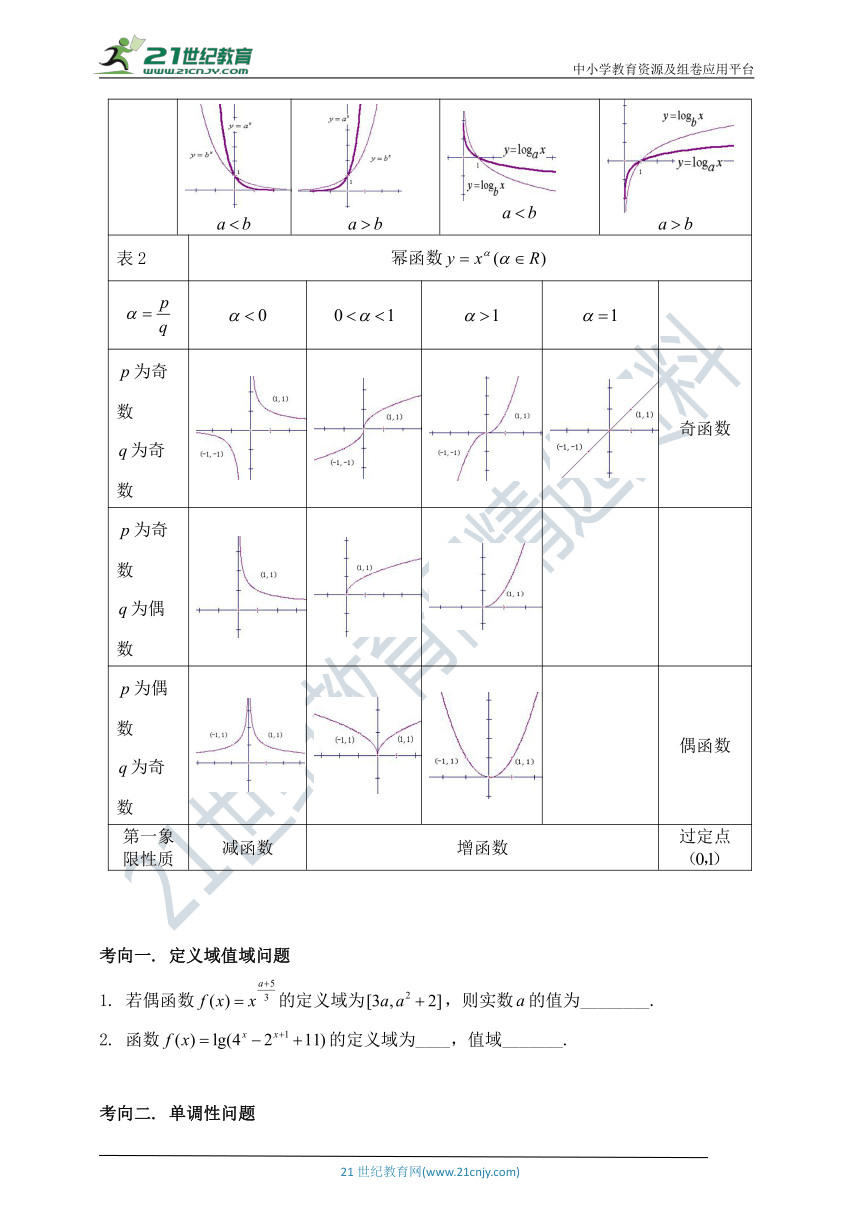
学案 指对幂综合
表1 指数函 对数数函
定义域
值域
图象
性质 过定点 过定点[:]
减函数 增函数 减函数 增函数
表2 幂函数
为奇数为奇数 奇函数
为奇数为偶数
为偶数为奇数 偶函数
第一象限性质 减函数 增函数 过定点
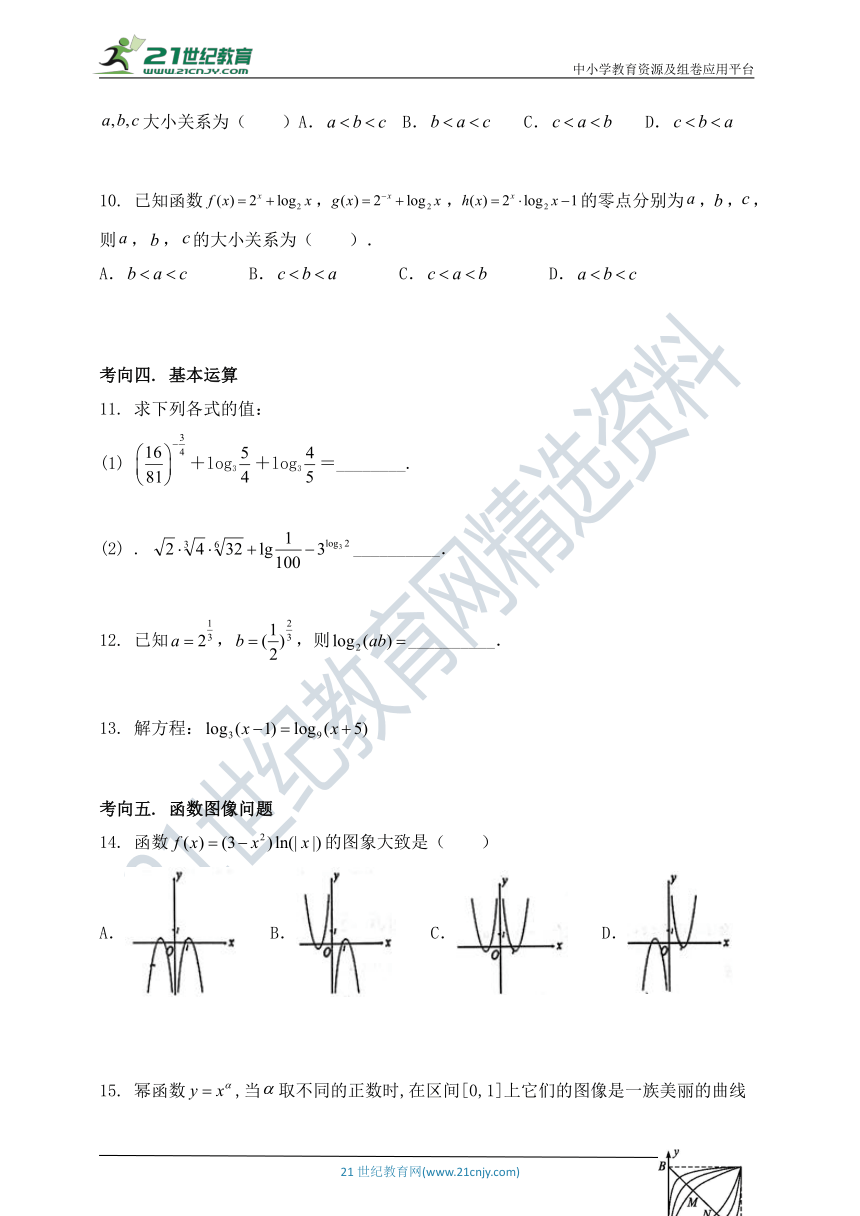
考向一. 定义域值域问题
若偶函数的定义域为,则实数的值为________.
函数的定义域为____,值域_______.
考向二. 单调性问题
已知在上是增函数,则实数的取值范围_____.
已知函数在区间上是增函数,则实数的取值范围是______.
已知函数(为常数)
若常数且,求的定义域
若,求函数的值域。
考向三. 比较大小
(1)、换元法 (2)、化同底指数幂 (3)、图象法 (4)、构造中间量法 (5)、直接利用函数的单调性 (6)、直接利用函数的单调性
三个数0.32,log20.3,20.3的大小顺序是( )
log20.3<20.3<0.32 B.0.32<log20.3<20.3 C.log20.3<0.32<20.3 D.0.32<20.3<log20.3
设a,b,c均为正数,且,,.则a,b,c大小顺序为( )
a<c<b B.b<c<a C.c<b<a D.a<b<c
已知且,若,则,,的大小关系为( )
B. C. D.
9. 设奇函数在上是增函数,若,,,则大小关系为( )A. B. C. D.
10. 已知函数,,的零点分别为,,,则,,的大小关系为( ).
B. C. D.
考向四. 基本运算
求下列各式的值:
+log3+log3=________.
. __________.
已知,,则__________.
解方程:
考向五. 函数图像问题
函数的图象大致是( )
A. B. C. D.
幂函数,当取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数,的图像三等分,即有,那么,等于_____.?
已知函数且点(4,2)在函数f(x)的图象上.
(1)求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;
(2)求不等式f(x)<1的解集;
(3)若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.
考向六. 分段函数问题
已知函数则=________.
设函数若,则的取值范围是
B. C. D.
已知函数,若对任意的,且都有成立,则实数的取值范围是________.
20. 已知函数(,且)是上的减函数,则实数的取值范围是_____.
21. 已知函数若,是互不相同的正数,且,则的取值范围是_____.
综合问题
已知函数,若f(x)为奇函数,则a= .
?
已知函数,则( )
B. C. D.
已知,,则的取值范围是( )
B. C. D.
已知幂函数是奇函数,且.
(1)求的值,并确定的解析式;
(2)求的值域.
已知函数是偶函数.
(1)求的值;
(2)设,若函数与的图像有且只有一个公共点,求实数的取值范围.
设为奇函数,为常数.
(1)确定的值(2)求证:是上的增函数
(3)若对于区间上的每一个值,不等式恒成立,求实数取值范围.
答案
-1
,
(1) (2)
解:∵0<0.32<0.30=1,log20.3<log21=0,1=20<20.3,∴,故选:C.
解:∵a>0,∴=,∴.∵b>0,∴,∴,∴.∵c>0,∴0<,∴1<c<2.
综上可知:a<b<c.故选:D.
A
由且可得,∵,∴.又由,得,
∴.∴,∴.
D
解:由为奇函数,且在上是增函数,可得,可得,且,,由,可得,故,
D
令,则.令,则.令,则,.所以函数,,的零点可以转化为求函数与函数与函数,,的交点,如图所示,可知,,
∴.
(1).
【解析】原式。
(2)===4﹣4=0.
由题 即答案为.
A
已知函数,==,即函数是偶函数,故排除选项B,D;
由,得或 ,
当x>0时, ,,可排除选项C,故选A.
1.
由条件,得M,N,可得,即α=lo,β=lo.所以αβ=lo·lo=1.
(1)见解析; (2);(3).
(1)∵点在函数的图象上,
∴,∴.∴ .
画出函数的图象如下图所示.
(2)不等式等价于或解得,或,
所以原不等式的解集为.
(3)∵方程f(x)-2m=0有两个不相等的实数根,∴函数的图象与函数的图象有两个不同的交点.
结合图象可得,解得∴实数的取值范围为.
D
先画出函数的图象,如图所示:
因为互不相同,不妨设,且,
而,即有,可得,则,
由,且,可得,
且,
当时,,此时,但此时b,c相等,
故的范围为.
故答案为:.
(一)∵f(x)的定义域为R,且f(x)为奇函数,∴f(0)=0,.∴a=.经检验a=满足要求.
(二)∵f(x)为奇函数,∴f(-x)=-f(x),即a--a,解得a=.
A
由题得,令,则
所以,从而可知是奇函数所以 ,即所以
C
令则,∴,
又,…∴①,∴…②∴①②得.
则.
解:(1)∵幂函数f(x)=x(m∈Z)是奇函数,且f(1)<f(2).
∴﹣2m2+m+3是正奇数,且m∈Z,∴m=0,f(x)=x3.
(2)y=log22f(x)+log[2f(x)]==(3log2x)2+log2+logx3
=9(log2x)2﹣3log2x﹣1=9(log2x﹣)2﹣,∵x∈[],∴﹣1≤log2x≤1,
∴当log2x=时,y取最小值﹣,当log2x=﹣1时,y取最大值11.
∴y=log22f(x)+log[2f(x)],x∈[]的值域为[﹣,11].
解(1)∵函数f(x)=log4(4x+1)+kx(k∈R))是偶函数∴f(﹣x)=log4(4﹣x+1)﹣kx)=log4()﹣kx=log4(4x+1)+kx(k∈R)恒成立∴﹣(k+1)=k,则k=.
(2)g(x)=log4(a?2x﹣a),函数f(x)与g(x)的图象有且只有一个公共点,即
方程f(x)=g(x)只有一个解,由已知得log4(4x+1)x=log4(a?2x﹣a),
∴log4()=log4(a?2x﹣a),方程等价于,
设2x=t,t>0,则(a﹣1)t2﹣﹣1=0有一解,若a﹣1>0,设h(t)=(a﹣1)t2﹣﹣1,
∵h(0)=﹣1<0,∴恰好有一正解∴a>1满足题意
若a﹣1=0,即a=1时,h(t)=﹣﹣1,由h(t)=0,得t=﹣<0,不满足题意
若a﹣1<0,即a<1时,由,得a=﹣3或a=,
当a=﹣3时,t=满足题意当a=时,t=﹣2(舍去)
综上所述实数a的取值范围是{a|a>1或a=﹣3}.
解:(1)∵f(x)是奇函数,∴定义域关于原点对称,由>0,得(x﹣1)(1﹣ax)>0.令(x﹣1)(1﹣ax)=0,得x1=1,x2=,∴=﹣1,解得a=﹣1.
(2)由(1)f(x)=,令u(x)==1+,设任意x1<x2,且x1,x2∈(1,+∞),
则u(x1)﹣u(x2)=,∵1<x1<x2,∴x1﹣1>0,x2﹣1>0,x2﹣x1>0,
∴u(x1)﹣u(x2)>0,即u(x1)>u(x2).∴u(x)=1+(x>1)是减函数,
又y=u为减函数,∴f(x)在(1,+∞)上为增函数.
(3)由题意知﹣()x>m,x∈(3,4)时恒成立,令g(x)=﹣()x,x∈(3,4),由(2)知在[3,4]上为增函数,又﹣()x在(3,4)上也是增函数,
故g(x)在(3,4)上为增函数,∴g(x)的最小值为g(3)=﹣,∴m<﹣,故实数m的范围是(﹣∞,﹣).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
