3.1.1方程的根与函数的零点(一元二次方程根的分布) 学案
文档属性
| 名称 | 3.1.1方程的根与函数的零点(一元二次方程根的分布) 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学案 一元二次方程根的分布
知识要点
依据函数零点与方程实数根的联系,可以用函数零点的存在性定理及二次函数的图像来讨论医一元二次方程的实数根的分布情况。
设方程的不等两根为且,相应的二次函数为,方程的根即为二次函数图像与x轴的交点的横坐标(也即是函数的零点),它们的分布情况见下面各表:
表一:两根与0的大小比较即根的正负情况(a>0)
分布情况 两个负根,即两根都小于0() 两个正根,即两根都大于0() 一正根一负根,即一个根小于0,一个大于0,
大致图像
结论
表二:两根与k的大小比较(a>0)
分布情况 两根都小于k 即 两根都大于k 即 一个根小于k,一个大于k即
大致图像
结论
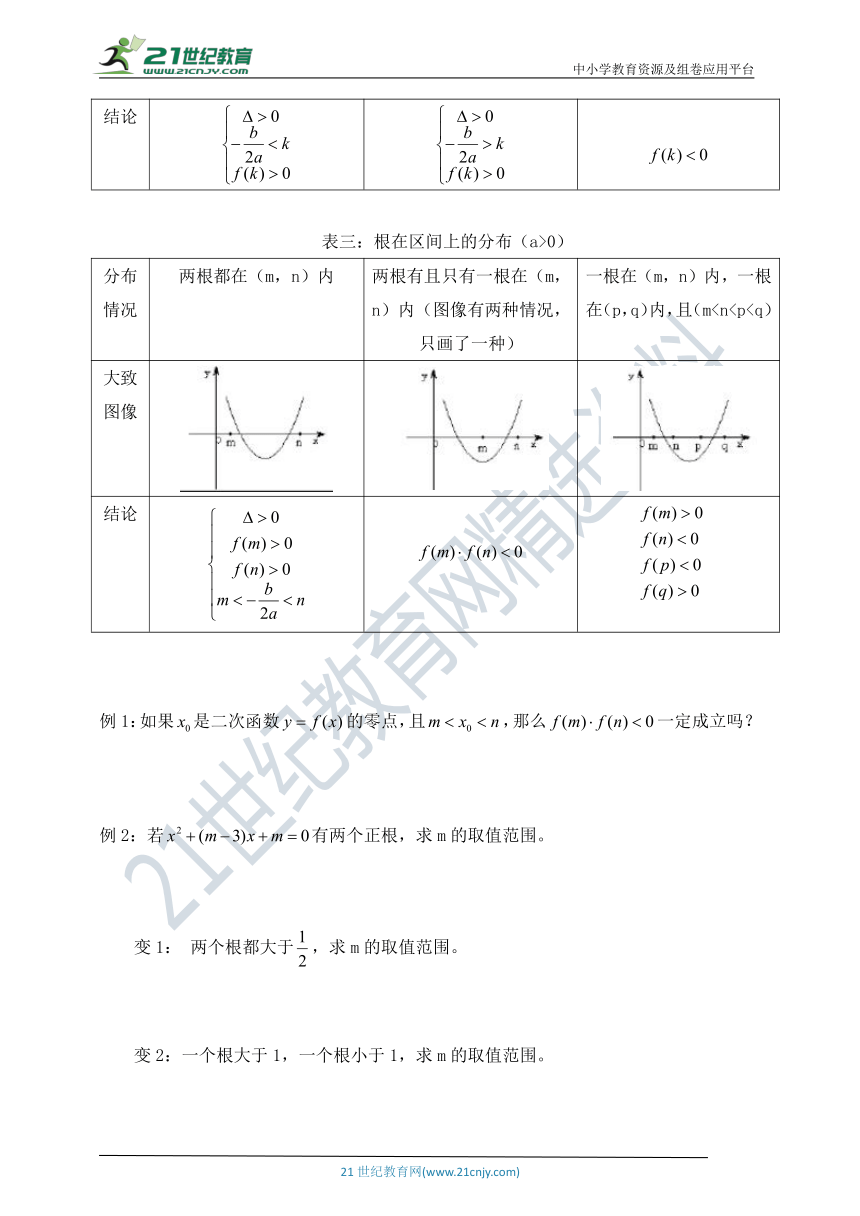
表三:根在区间上的分布(a>0)
分布情况 两根都在(m,n)内 两根有且只有一根在(m,n)内(图像有两种情况,只画了一种) 一根在(m,n)内,一根在(p,q)内,且(m
结论
例1:如果是二次函数的零点,且,那么一定成立吗?
例2:若有两个正根,求m的取值范围。
变1: 两个根都大于,求m的取值范围。
变2:一个根大于1,一个根小于1,求m的取值范围。
变3:一个根在(-2 ,0)内,另一个根在(0 ,4)内,求m的取值范围。
例3:若方程在内恰有一解,则的取值范围为( ?)
A. B. C. D.
变1:关于的方程在区间(0,2)上有唯一实根,则实数的取值范围为 。
变2:若方程在区间(0,1)上有且仅有一根,则实数的取值范围是( )
A.? B.? C. D.
例4:已知a是实数,函数,如果函数在区间上有零点,则a的取值范围是 。
变1:已知函数有且仅有一个正实数的零点,则实数m的取值范围是 。
变2:若函数在区间[0,4]内至少有一个零点,则实数a的取值范围是 。
参考答案
例1:
【解析】:不一定成立,如图:
对于函数来说,是它的零点。若,则恒有成立。
例2:
【解析】:
变1:
【解析】:
变2:
【解析】:
变3:
【解析】:
例3:
【解析】:,,
由得,又当,即时,两根,不合题意,
【答案】B.
变1:
【解析】
②当
②当
综上:
变2:【解析】方程在区间上有且仅有一个根,则,
即,,解得.
【答案】B
例4:【解析】①a=0时,,令得上无零点,不符合题意,故
②当时,的图像的对称轴为直线
当?
当
③当,
当
当?
综上所述,a的取值范围是
变1:【解析】当时,零点,满足题意
当时,解得且
设是函数两个零点,则,
若,函数只有一个零点1,满足题意
若,则均为正数,不符合题意,舍去
若,则一正一负,满足题意
综上,实数m的取值范围是
【答案】
变2:【解析】因为函数在区间[0,4]内至少有一个零点,且,结合函数的 图像(图略),所以或,解得或,即,所以实数a的取值范围为。
【答案】
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
