人教新课标A版 必修1 阅读与思考 对数的发明 课件24张PPT
文档属性
| 名称 | 人教新课标A版 必修1 阅读与思考 对数的发明 课件24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:05:33 | ||
图片预览







文档简介
课件24张PPT。数学史珍闻
——对数的发明1.阅读材料,理清脉络学生阅读必修1 P68的“阅读与思考”,并回答以下问题
【问题1】对数是在什么背景下发明的,它的发明对社会产生了怎样的影响?
【问题2】对数的发明者是谁?你能理解他所描述的对数定义吗?
【问题3】谁令对数更为广泛的流传?他采用了什么方法改进?
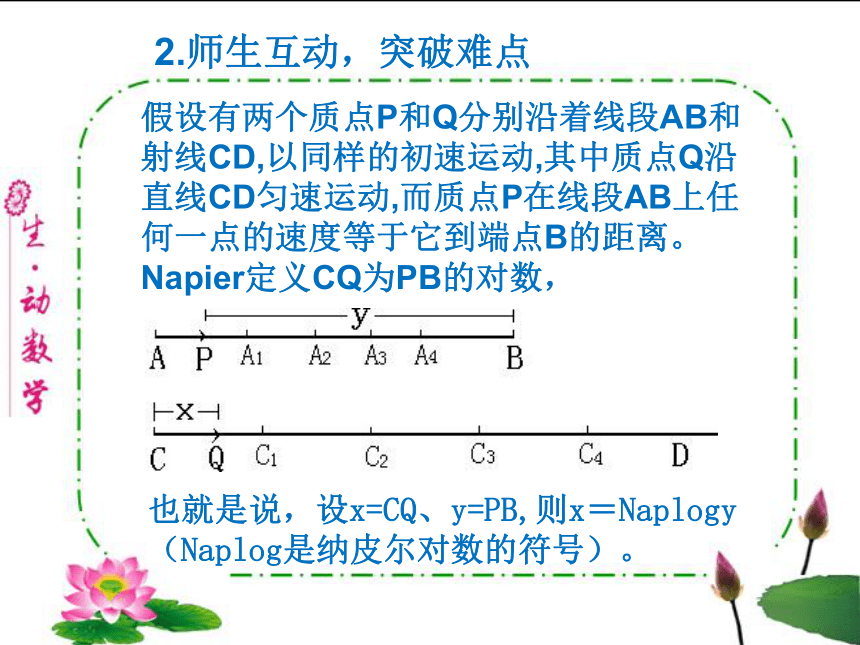
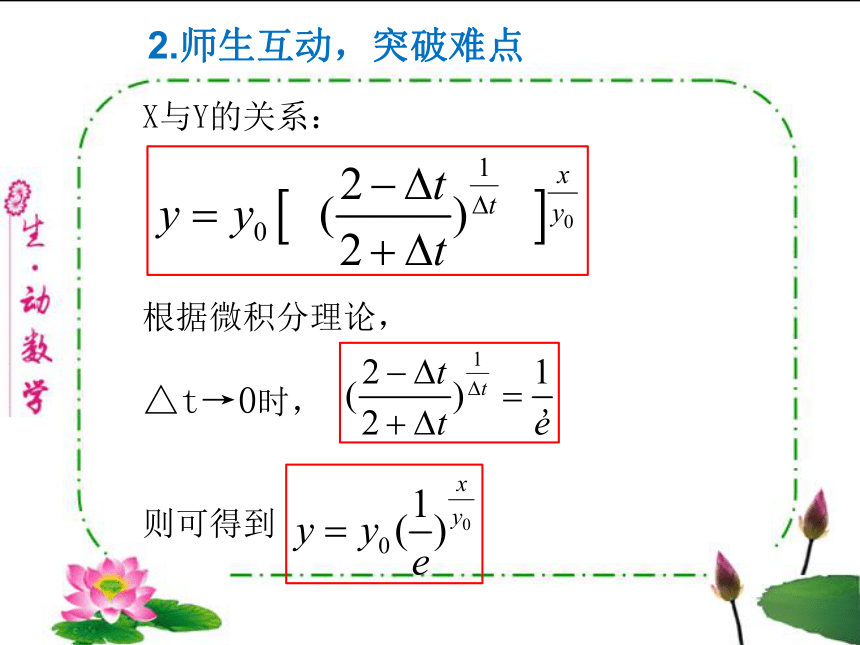
【问题4】为什么对数的运算不是在由指数推出?谁发现了指数与对数的关系?2.师生互动,突破难点假设有两个质点P和Q分别沿着线段AB和射线CD,以同样的初速运动,其中质点Q沿直线CD匀速运动,而质点P在线段AB上任何一点的速度等于它到端点B的距离。Napier定义CQ为PB的对数,也就是说,设x=CQ、y=PB,则x=Naplogy(Naplog是纳皮尔对数的符号)。当P和Q从A和C出发时,其初速度的数值等于线段AB的长度(设为y0),此后在相等时间间隔情况下,时刻t1,t2,t3,t4 ,?时, Q位于C1,C2,C3,C4,?,P位于A1,A2,A3,A4,?。由于Q沿CD做匀速运动,C,C1,C2,C3,C4,?,是等距的,2.师生互动,突破难点2.师生互动,突破难点Q与端点C的距离形成等差数列 0,y0△t,2y0△t,3y0△t,4y0△t,?,而A,A1,A2,A3,A4,?与端点B的距离形成等比数列如何建立x与y的函数关系呢?2.师生互动,突破难点X与Y的关系:
根据微积分理论,
△t→0时, ,
则可得到Napier认为,质点运动的时间间隔△t应尽量小,他选择了
相应
为了避免小数的麻烦,他又规定 ,Napier的核心思想是从等差数列与等比数列的关系中定义对数, Napier没有底的概念。他从连续的几何量出发,定义的对数是连续的. 由数列定义的对数是离散的。3.对比运算,体验简便常用对数表使用说明
1、整数部分是一位非零数字。
lg2.573:在第1列找25再横行找“7”为4099,修正值“3”为5。所以lg2.573=0.4104。
2、整数部分不是一位非零数字的。用科学记数法表示N×10n。
lg25730=lg(2.573×104)=lg2.573+4=4.4104。lg0.002573=lg[2.573×10-3]
=lg2.573+(-3)= -2.5896.
3、查反对数时。正小数部分查表,整数
部分决定小数点的位置。
6.4104:由0.4104查出0.4104=lg2.573。
则6.4104=lg2.573+6=lg(2.573×10*6)
=lg2573000。
负的对数化负整数+正纯小数。再同样查。 常用对数表的运用例1.运用对数运算原理,计算17951235×0.08304115解:设17951235=aX, 0.08304115=aY,则17951235×0.08304115=aX ×aY=aX+Y。这里x是17951235的(以a为底的)对数,y是0.08304115的(以a为底的)对数。底a是可以任意指定的,我们指定a=10,则只要查表得到这二个数的常用对数(以10为底的对数称为常用对数) x=lg17951235=7.2540943323和y=lg0.08304115=-1.0807066451,计算x+y=6.1733876872,再查表得
6.1733876872的(以10为底的)指数
函数,106.1733876872=1490691.1983
就得到了
1795123517951235×0.08304115的
乘积。【活动】不同方式竞赛算 8347×23.45
一位用乘法,
一位用对数查表法,
一位用计算器,
一位计时【思考1】你能否从指数运算的角度推到对数运算,实现由乘除运算转为加减运算?4.运算互推,清楚本源【思考2】在你的学习过程中是否有加减运算与乘除运算互换的体验小学是学习的乘法是加法的简便运算,减法实则是加法的逆运算;
不等式中只有加法与乘法运算,没有减法和除法运算;
向量与向量只有加法运算、减法运算和数量积运算;
【思考2】在你的学习过程中是否有加减运算与乘除运算互换的体验
5.符号体系,减负思维
如,阿拉伯数字的引用;杨辉三角与帕斯卡三角;刘辉割圆术与祖冲之的圆周率【思考3】在“阅读与思考”中,较好的符
号体系对于数学的发展是至关重要的,对此
你有怎样的体会?
知识与技能:
过程与方法:
情感态度价值观:6.小结内容,提炼思想
——对数的发明1.阅读材料,理清脉络学生阅读必修1 P68的“阅读与思考”,并回答以下问题
【问题1】对数是在什么背景下发明的,它的发明对社会产生了怎样的影响?
【问题2】对数的发明者是谁?你能理解他所描述的对数定义吗?
【问题3】谁令对数更为广泛的流传?他采用了什么方法改进?
【问题4】为什么对数的运算不是在由指数推出?谁发现了指数与对数的关系?2.师生互动,突破难点假设有两个质点P和Q分别沿着线段AB和射线CD,以同样的初速运动,其中质点Q沿直线CD匀速运动,而质点P在线段AB上任何一点的速度等于它到端点B的距离。Napier定义CQ为PB的对数,也就是说,设x=CQ、y=PB,则x=Naplogy(Naplog是纳皮尔对数的符号)。当P和Q从A和C出发时,其初速度的数值等于线段AB的长度(设为y0),此后在相等时间间隔情况下,时刻t1,t2,t3,t4 ,?时, Q位于C1,C2,C3,C4,?,P位于A1,A2,A3,A4,?。由于Q沿CD做匀速运动,C,C1,C2,C3,C4,?,是等距的,2.师生互动,突破难点2.师生互动,突破难点Q与端点C的距离形成等差数列 0,y0△t,2y0△t,3y0△t,4y0△t,?,而A,A1,A2,A3,A4,?与端点B的距离形成等比数列如何建立x与y的函数关系呢?2.师生互动,突破难点X与Y的关系:
根据微积分理论,
△t→0时, ,
则可得到Napier认为,质点运动的时间间隔△t应尽量小,他选择了
相应
为了避免小数的麻烦,他又规定 ,Napier的核心思想是从等差数列与等比数列的关系中定义对数, Napier没有底的概念。他从连续的几何量出发,定义的对数是连续的. 由数列定义的对数是离散的。3.对比运算,体验简便常用对数表使用说明
1、整数部分是一位非零数字。
lg2.573:在第1列找25再横行找“7”为4099,修正值“3”为5。所以lg2.573=0.4104。
2、整数部分不是一位非零数字的。用科学记数法表示N×10n。
lg25730=lg(2.573×104)=lg2.573+4=4.4104。lg0.002573=lg[2.573×10-3]
=lg2.573+(-3)= -2.5896.
3、查反对数时。正小数部分查表,整数
部分决定小数点的位置。
6.4104:由0.4104查出0.4104=lg2.573。
则6.4104=lg2.573+6=lg(2.573×10*6)
=lg2573000。
负的对数化负整数+正纯小数。再同样查。 常用对数表的运用例1.运用对数运算原理,计算17951235×0.08304115解:设17951235=aX, 0.08304115=aY,则17951235×0.08304115=aX ×aY=aX+Y。这里x是17951235的(以a为底的)对数,y是0.08304115的(以a为底的)对数。底a是可以任意指定的,我们指定a=10,则只要查表得到这二个数的常用对数(以10为底的对数称为常用对数) x=lg17951235=7.2540943323和y=lg0.08304115=-1.0807066451,计算x+y=6.1733876872,再查表得
6.1733876872的(以10为底的)指数
函数,106.1733876872=1490691.1983
就得到了
1795123517951235×0.08304115的
乘积。【活动】不同方式竞赛算 8347×23.45
一位用乘法,
一位用对数查表法,
一位用计算器,
一位计时【思考1】你能否从指数运算的角度推到对数运算,实现由乘除运算转为加减运算?4.运算互推,清楚本源【思考2】在你的学习过程中是否有加减运算与乘除运算互换的体验小学是学习的乘法是加法的简便运算,减法实则是加法的逆运算;
不等式中只有加法与乘法运算,没有减法和除法运算;
向量与向量只有加法运算、减法运算和数量积运算;
【思考2】在你的学习过程中是否有加减运算与乘除运算互换的体验
5.符号体系,减负思维
如,阿拉伯数字的引用;杨辉三角与帕斯卡三角;刘辉割圆术与祖冲之的圆周率【思考3】在“阅读与思考”中,较好的符
号体系对于数学的发展是至关重要的,对此
你有怎样的体会?
知识与技能:
过程与方法:
情感态度价值观:6.小结内容,提炼思想
