人教新课标A版 必修1 第三章 函数的应用 阅读与思考 函数概念的发展历程课件27张PPT
文档属性
| 名称 | 人教新课标A版 必修1 第三章 函数的应用 阅读与思考 函数概念的发展历程课件27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:06:11 | ||
图片预览








文档简介
课件27张PPT。函 数 概 念 发 展 史几何框架下的函数概念
前期发展其实早在14世纪,法国数学家奥拉斯特在表示因时间t而变的变数x时,就画出了图形,只建立起了孤立的点与点的对应,后来被开普勒和伽利略运用于天体方面的研究
随着时间的推移,人们对动点轨迹的研究越发深入,生产和科学技术的发展要求数学不仅研究静止不动的量,更要研究运动过程中各个量之间的依赖关系,促使数学从常量数学时期,进入到变量数学时期
函数是研究变量数学必不可少的概念
用文字和比例的语言表达函数的关系包含函数或称为变量关系这一概念 笛卡尔大部分函数被当做曲线来研究注意到一个变量对另一个变量的依赖关系,只是尚未意识到提炼函数概念 莱布尼茨
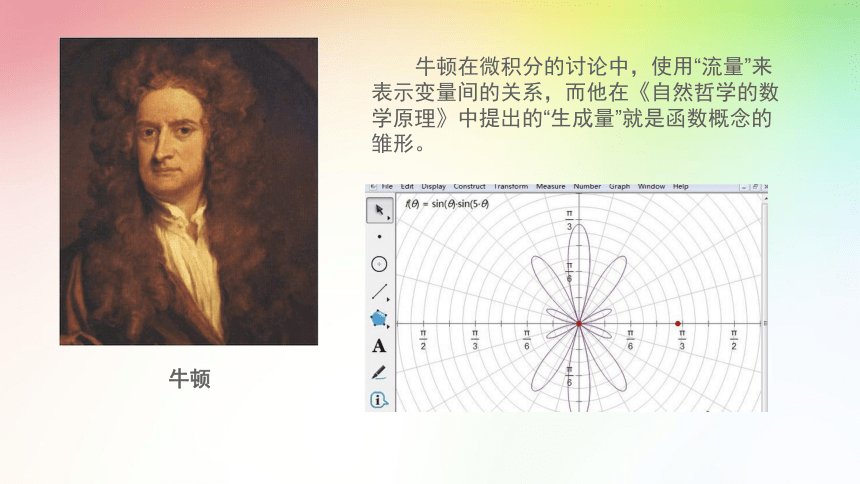
Function幂 v牛顿 牛顿在微积分的讨论中,使用“流量”来表示变量间的关系,而他在《自然哲学的数学原理》中提出的“生成量”就是函数概念的雏形。18世纪的新函数概念18世纪——函数的黄金时代1718年,瑞士数学家约翰·柏努利在莱布尼兹函数概念的基础上,对函数概念进行了定义:“由任一变量和常数的任一形式所构成的量。”18世纪解析函数的发展1755.莱昂纳多‘欧拉“若某些量以如下方式依赖于另一些量 ,即当后者变化时前者也随之而变化 ,则称前量是后量的函数”。 1718.约翰’伯努利“变量 的函数就是变量和常数以任何方式组成的表达式,记作X” 1748.莱昂纳多‘欧拉 “变量”的函数是一个解析表达式 , 它是这个“变量”和 一 些常数以任何方式组成的 新概念下的函数之美新概念下的函数之美优美的函数图像对应关系下的函数概念 若当x的某个值,都有完全确定的y值与之对应,则称y是x的函数。其中x叫做自变量。“变化”第一次出现了自变量一词柯西体现了函数的本质
一一对应 函数的定义:设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数, 记作 y=f(x) , x∈A x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域。
前期发展其实早在14世纪,法国数学家奥拉斯特在表示因时间t而变的变数x时,就画出了图形,只建立起了孤立的点与点的对应,后来被开普勒和伽利略运用于天体方面的研究
随着时间的推移,人们对动点轨迹的研究越发深入,生产和科学技术的发展要求数学不仅研究静止不动的量,更要研究运动过程中各个量之间的依赖关系,促使数学从常量数学时期,进入到变量数学时期
函数是研究变量数学必不可少的概念
用文字和比例的语言表达函数的关系包含函数或称为变量关系这一概念 笛卡尔大部分函数被当做曲线来研究注意到一个变量对另一个变量的依赖关系,只是尚未意识到提炼函数概念 莱布尼茨
Function幂 v牛顿 牛顿在微积分的讨论中,使用“流量”来表示变量间的关系,而他在《自然哲学的数学原理》中提出的“生成量”就是函数概念的雏形。18世纪的新函数概念18世纪——函数的黄金时代1718年,瑞士数学家约翰·柏努利在莱布尼兹函数概念的基础上,对函数概念进行了定义:“由任一变量和常数的任一形式所构成的量。”18世纪解析函数的发展1755.莱昂纳多‘欧拉“若某些量以如下方式依赖于另一些量 ,即当后者变化时前者也随之而变化 ,则称前量是后量的函数”。 1718.约翰’伯努利“变量 的函数就是变量和常数以任何方式组成的表达式,记作X” 1748.莱昂纳多‘欧拉 “变量”的函数是一个解析表达式 , 它是这个“变量”和 一 些常数以任何方式组成的 新概念下的函数之美新概念下的函数之美优美的函数图像对应关系下的函数概念 若当x的某个值,都有完全确定的y值与之对应,则称y是x的函数。其中x叫做自变量。“变化”第一次出现了自变量一词柯西体现了函数的本质
一一对应 函数的定义:设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数, 记作 y=f(x) , x∈A x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域。
