2.2.1 对数与对数运算 课件24张PPT
文档属性
| 名称 | 2.2.1 对数与对数运算 课件24张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 23:34:27 | ||
图片预览








文档简介
课件24张PPT。进入2.2.1 对数 截止到1999年底,我国人口约13亿.如果今后能将人口年平均增长率控制在1%,那么经过多少年后我国人口数约为18亿?分析:设经过X年,则有:整理得: 一.新课引入
探究2,3,8之间存在的运算关系① 2,3两个数通过什么运算可以得到8?如何表示? ② 8,3两个数通过什么运算可以得到2?如何表示?③ 2,8两个数通过什么运算可以得到3?如何表示? 答:2的3次方等于8,是乘方运算,表示为:答:8的3次方根等于2是开方运算,表示为:怎么办?怎么办?其中a叫做对数的底数,N叫做真数。一般地,如果 ,那么数x
叫做以 为底N的对数,记作注意:①底数的限制:a>0且a≠1
②对数的书写格式二.探索新知定义:一般地,如果 ,那么
数x叫做以 为底N的对数,记作例如: 1.为什么限制 ?对 数这是因为2. N能小于零或等于零吗?(不能,这是因为a>0,ax=N>0)强调真数大于零结论:对数式中真数要大于零。
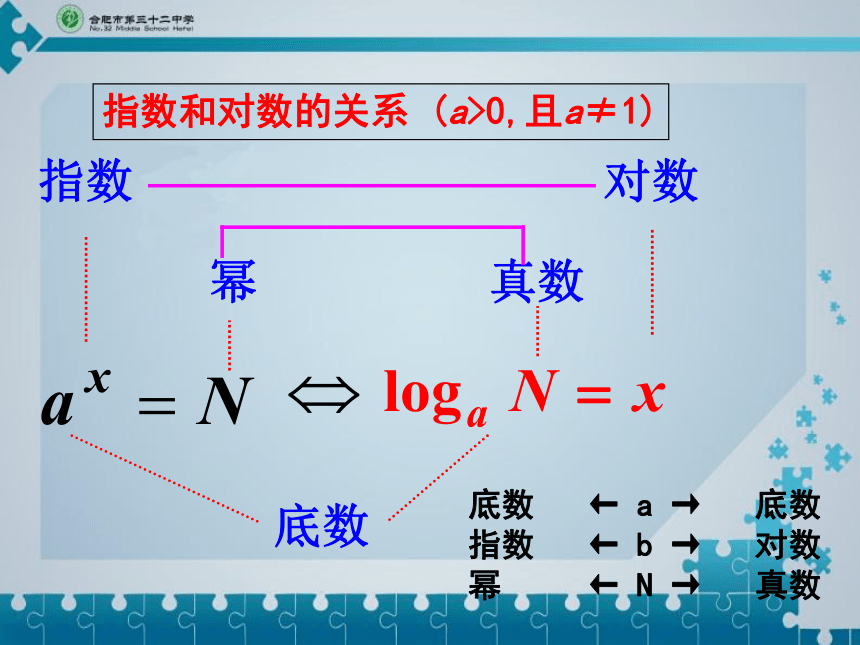
(也就是说零和负数没有对数!)底数幂真数指数对数指数和对数的关系 (a>0,且a≠1)底数 ← a → 底数
指数 ← b → 对数
幂 ← N → 真数 1、常用对数:以10为底的对数 简记为以e为底的对数2、自然对数:简记为你记住了吗?(e≈2.71828…)两个重要对数:(1) (3) (2) 例1:将下列指数式写成对数式,对数式写成
指数式:解:三.例题讲解与课堂练习(6) (5) (4) 指对数的互化关键是抓住对数式和指数式的关系,弄清楚各个量在对应式子中扮演的角色。把下列指数式写成对数式: 2.把下列对数式写成指数式:
知识扩展
对数的发明
对数的概念,首先是由苏格兰数学家John Napier(纳皮尔,1550~1617)提出的。那时候天文学是热门学科。可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间。Napier也是一位天文爱好者,经20年潜心研究大数的计算技术,他终于独立发明了对数.开普勒利用对数表简化了行星轨道的复杂计算。恩格斯把对数的发明称为17世纪数学的三大成就之一.伽利略发出了豪言壮语:“给我时间、空间和对数,我可以创造出一个宇宙来。”数学家拉普拉斯说:“对数用缩短计算的时间来使天文学家的寿命加倍”。而天文学家更是以近乎狂喜的心情来迎接这一发明. (1)解:∵求真数
例2:求下列各式中x的值 :解:∵∴ 求底数
∴∴求对数
∴解:四、对数的性质 探究活动1
求下列各式的值: 0 0 0 0 思考:你发现了什么?“1”的对数等于零,即 等价探究活动2
求下列各式的值:四、对数的性质 1 1 1 1 思考:你发现了什么?底数的对数等于1,即 等价 1、负数和零没有对数
2、3、 ③ 2,8两个数通过什么运算可以得到3?
如何表示?答:以2为底8的对数等于3,是对数运算,
如何表示为:计算器计算得:请完成P64页练习3、4 五、课堂练习1、知识小结 一般地,如果 ,那么数
叫做以 为底N的对数,记作
其中 叫做对数的底数, 叫做真数 。 (1)对数的概念(2)两类特殊对数六.课堂小结(3)对数与指数间的关系 当 时,(4)对数的基本性质零和负数0110 (1)指对数的互化关键是抓住对数式和指数式的关系,弄清楚各个量在对应式子中扮演的角色。2、方法小结(2)对数本质上就是“求指数”。 Thank you for listening!
叫做以 为底N的对数,记作注意:①底数的限制:a>0且a≠1
②对数的书写格式二.探索新知定义:一般地,如果 ,那么
数x叫做以 为底N的对数,记作例如: 1.为什么限制 ?对 数这是因为2. N能小于零或等于零吗?(不能,这是因为a>0,ax=N>0)强调真数大于零结论:对数式中真数要大于零。
(也就是说零和负数没有对数!)底数幂真数指数对数指数和对数的关系 (a>0,且a≠1)底数 ← a → 底数
指数 ← b → 对数
幂 ← N → 真数 1、常用对数:以10为底的对数 简记为以e为底的对数2、自然对数:简记为你记住了吗?(e≈2.71828…)两个重要对数:(1) (3) (2) 例1:将下列指数式写成对数式,对数式写成
指数式:解:三.例题讲解与课堂练习(6) (5) (4) 指对数的互化关键是抓住对数式和指数式的关系,弄清楚各个量在对应式子中扮演的角色。把下列指数式写成对数式: 2.把下列对数式写成指数式:
知识扩展
对数的发明
对数的概念,首先是由苏格兰数学家John Napier(纳皮尔,1550~1617)提出的。那时候天文学是热门学科。可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间。Napier也是一位天文爱好者,经20年潜心研究大数的计算技术,他终于独立发明了对数.开普勒利用对数表简化了行星轨道的复杂计算。恩格斯把对数的发明称为17世纪数学的三大成就之一.伽利略发出了豪言壮语:“给我时间、空间和对数,我可以创造出一个宇宙来。”数学家拉普拉斯说:“对数用缩短计算的时间来使天文学家的寿命加倍”。而天文学家更是以近乎狂喜的心情来迎接这一发明. (1)解:∵求真数
例2:求下列各式中x的值 :解:∵∴ 求底数
∴∴求对数
∴解:四、对数的性质 探究活动1
求下列各式的值: 0 0 0 0 思考:你发现了什么?“1”的对数等于零,即 等价探究活动2
求下列各式的值:四、对数的性质 1 1 1 1 思考:你发现了什么?底数的对数等于1,即 等价 1、负数和零没有对数
2、3、 ③ 2,8两个数通过什么运算可以得到3?
如何表示?答:以2为底8的对数等于3,是对数运算,
如何表示为:计算器计算得:请完成P64页练习3、4 五、课堂练习1、知识小结 一般地,如果 ,那么数
叫做以 为底N的对数,记作
其中 叫做对数的底数, 叫做真数 。 (1)对数的概念(2)两类特殊对数六.课堂小结(3)对数与指数间的关系 当 时,(4)对数的基本性质零和负数0110 (1)指对数的互化关键是抓住对数式和指数式的关系,弄清楚各个量在对应式子中扮演的角色。2、方法小结(2)对数本质上就是“求指数”。 Thank you for listening!
