2.2.2 对数函数及其性质课件39张PPT
文档属性
| 名称 | 2.2.2 对数函数及其性质课件39张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 810.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 00:00:00 | ||
图片预览








文档简介
课件39张PPT。对数函数及其性质湖南长沙马王堆汉墓女尸“辛追夫人”出土,考古学家们通过检验“夫人”身上的每一个碳14含量P,就可以推算出马王堆古墓的年代。思考: t 能不能看成是 P 的函数?导1.理解对数函数的定义.
2.会画出对数函数的图像,探索 研究对数函数图像及其性质 .
3.应用对数函数性质解决问题.导 教学重点难点教学目标重点:对数函数的图像与性质.
难点:底数对对数函数值变化的影响.思.议1.对数函数的定义.2.画出图像3.对数函数的图像与性质.一 定义.
一般地,函数y=loga x(a>0,且a≠ 1)叫 做对数函数.其中x是自变量,函数的定义域是(0 ,+∞).真数大于0(2) 2.下列两个函数为对数函数吗?注意:对数函数的定义与指数函数类似,都是
形式定义,注意辨别.评.讲作图步骤: ①列表,
②描点,
③连线。二,探索研究
对数函数:y = loga x (a>0,且a≠1)图像与性质学生活动1:用描点法画出下面函数的图像,并观察图像,
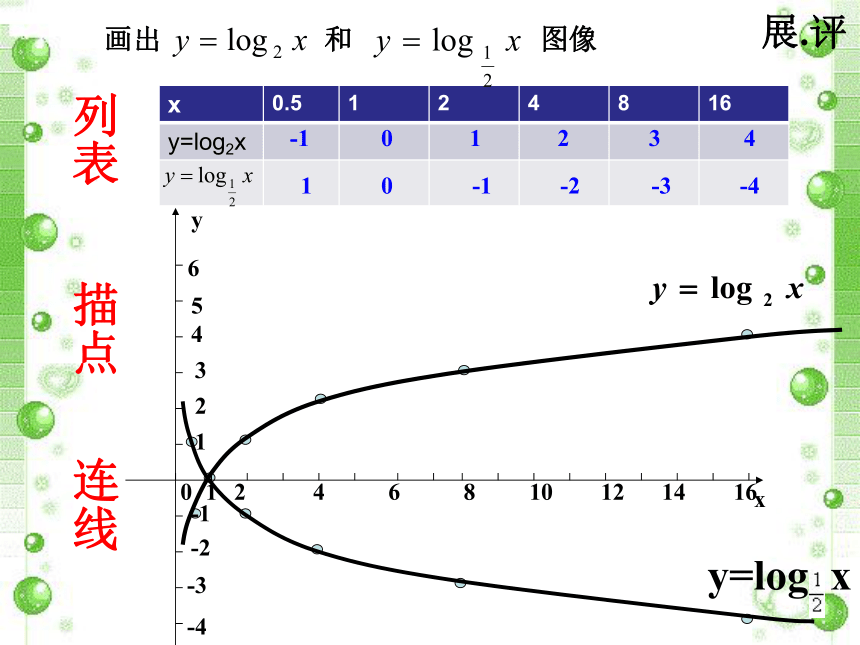
找出图像的特征,总结函数的性质.思.议-101234列表描点连线10-1-2-3-4展.评这两个函数的图像
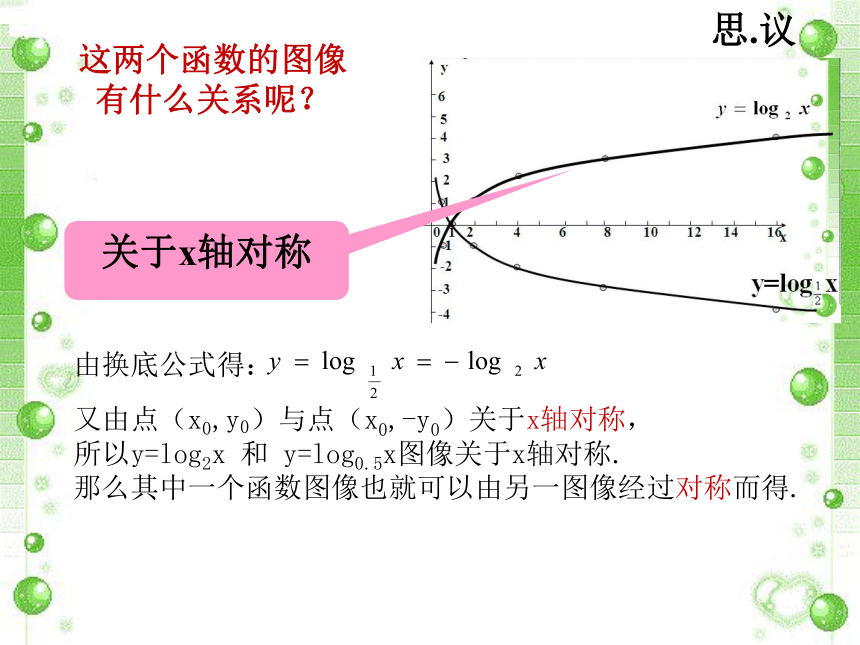
有什么关系呢?又由点(x0,y0)与点(x0,-y0)关于x轴对称,
所以y=log2x 和 y=log0.5x图像关于x轴对称.
那么其中一个函数图像也就可以由另一图像经过对称而得.关于x轴对称思.议三.探索.研究
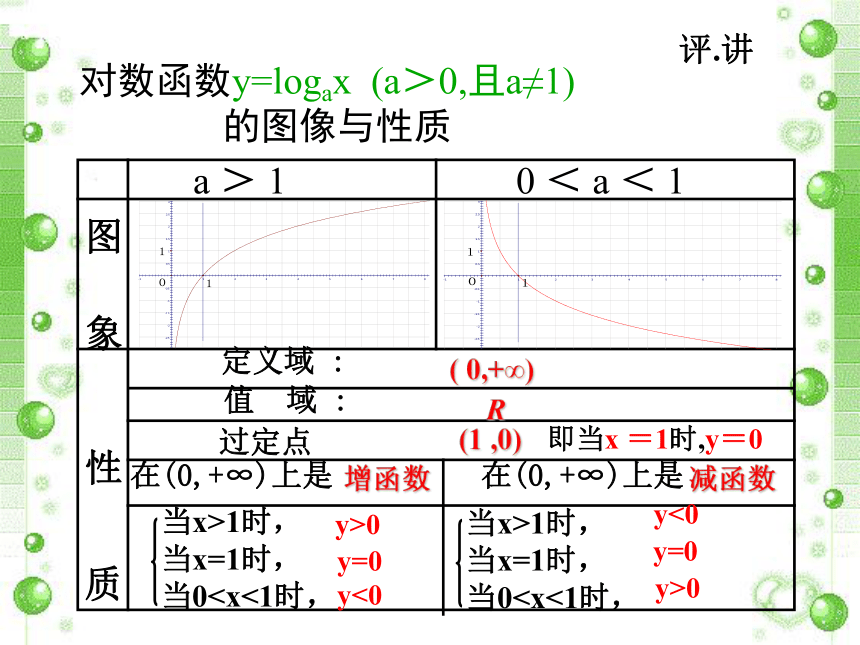
对数函数:y = loga x (a>0,且a≠1)图像与性质学生活动2: 选取底数a(a>0且a≠1)的若干个不同的值,在同一平面直角坐标系内作出相应的对数函数的图像.观察图像,你能发现它们有哪些共同特征吗?图像演示思.议 图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图像与性质( 0,+∞)R
(1 ,0) 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 评.讲例题讲解例1 求下列函数的定义域: 解:(1) ∵ 即 ,
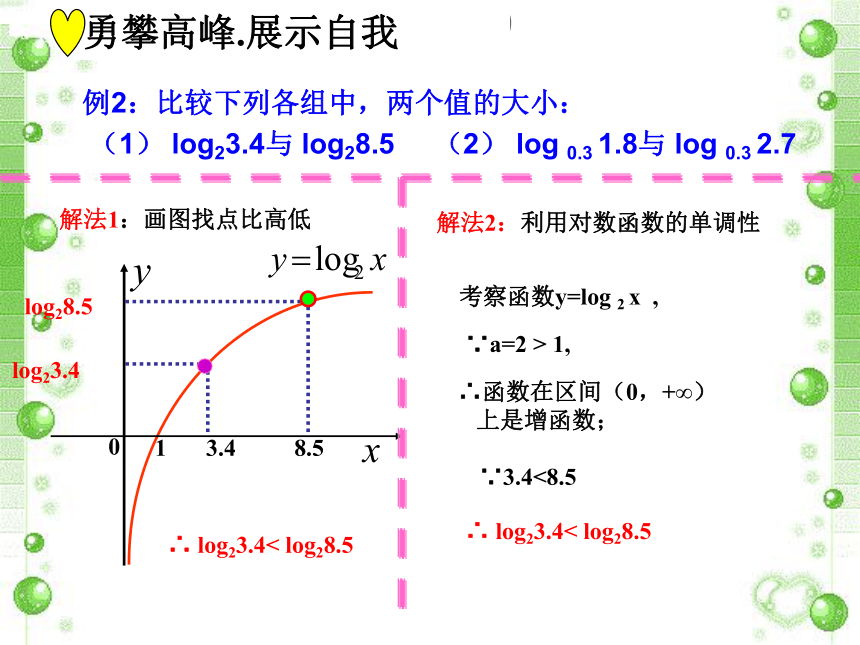
∴函数 的定义域是: 评.讲 →牛刀小试例2:比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5∴ log23.4< log28.5勇攀高峰.展示自我(2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 解法1:画图找点比高低注意:若底数不确定,那就要对底数进行分类讨论
即0 1比较下列各组中,两个值的大小:
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0∴ loga5.1 > loga5.9评.讲比较两个对数值的大小时:例题小结链接高考→能力提升(2010·天津高考文科·T6)设(A)a(1 ,0) 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 登高回望二.对数函数的图像和性质.三.比较两个对数值的大小.一.对数函数的定义.课堂小结四 .数形结合,分类讨论的思想.一个定义,两个图像,两种思想谢谢您的指导返回再来一遍
2.会画出对数函数的图像,探索 研究对数函数图像及其性质 .
3.应用对数函数性质解决问题.导 教学重点难点教学目标重点:对数函数的图像与性质.
难点:底数对对数函数值变化的影响.思.议1.对数函数的定义.2.画出图像3.对数函数的图像与性质.一 定义.
一般地,函数y=loga x(a>0,且a≠ 1)叫 做对数函数.其中x是自变量,函数的定义域是(0 ,+∞).真数大于0(2) 2.下列两个函数为对数函数吗?注意:对数函数的定义与指数函数类似,都是
形式定义,注意辨别.评.讲作图步骤: ①列表,
②描点,
③连线。二,探索研究
对数函数:y = loga x (a>0,且a≠1)图像与性质学生活动1:用描点法画出下面函数的图像,并观察图像,
找出图像的特征,总结函数的性质.思.议-101234列表描点连线10-1-2-3-4展.评这两个函数的图像
有什么关系呢?又由点(x0,y0)与点(x0,-y0)关于x轴对称,
所以y=log2x 和 y=log0.5x图像关于x轴对称.
那么其中一个函数图像也就可以由另一图像经过对称而得.关于x轴对称思.议三.探索.研究
对数函数:y = loga x (a>0,且a≠1)图像与性质学生活动2: 选取底数a(a>0且a≠1)的若干个不同的值,在同一平面直角坐标系内作出相应的对数函数的图像.观察图像,你能发现它们有哪些共同特征吗?图像演示思.议 图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图像与性质( 0,+∞)R
(1 ,0) 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 评.讲例题讲解例1 求下列函数的定义域: 解:(1) ∵ 即 ,
∴函数 的定义域是: 评.讲 →牛刀小试例2:比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5∴ log23.4< log28.5勇攀高峰.展示自我(2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 解法1:画图找点比高低注意:若底数不确定,那就要对底数进行分类讨论
即0
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0
