2.3.1 幂函数课件30张PPT
文档属性
| 名称 | 2.3.1 幂函数课件30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 23:36:57 | ||
图片预览







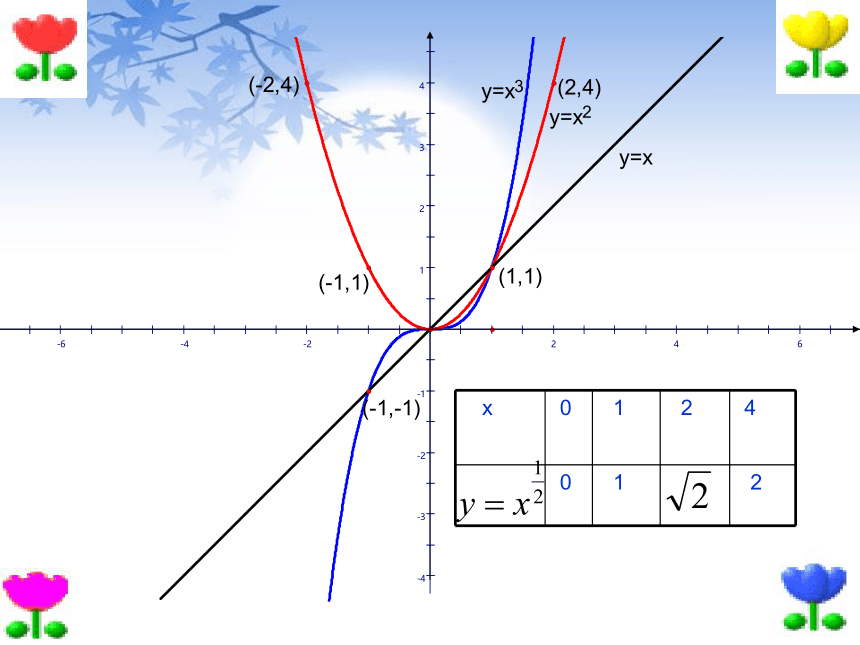
文档简介
课件30张PPT。幂 函 数高中数学必修1我国著名数学家华罗庚教授在其《数学的用场与发展》中指出: “宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。”
问题1:如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p = 元, 。
问题2:如果正方形的边长为a,那么正方形的面积 是S = , 。
问题3:如果立方体的边长为a,那么立方体的体积是V = , 。
问题4:如果正方形场地的面积为S,那么正方形的边长a= , 。
问题5:如果某人t s内骑车行进了1km,那么他骑车的平均速度v = , 。 w这里p是w的函数a2这里S是a的函数a3这里V是a的函数这里a是S的函数这里v是t的函数若将它们的自变量全部用x来表示,函数值用y来表示,则它们的函数关系式将是:引入观察引入:观察下列五组函数总结他们的共同特征共同特征:
1.形如
2.都是以自变量x为底数;
3.指数为常数;
4.前面的系数为1;
5.只有一项。
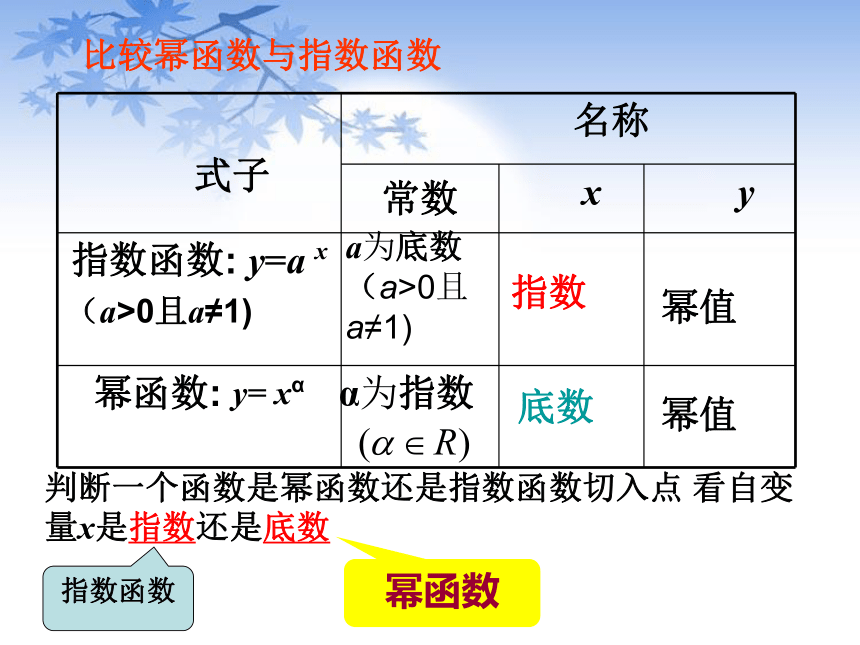
比较幂函数与指数函数a为底数(a>0且a≠1)
指数底数幂值幂值判断一个函数是幂函数还是指数函数切入点 看自变量x是指数还是底数幂函数指数函数 1.下列函数是幂函数的是 ( ).(1) y=x4 (3) y= -x2 (5) y=3x2 (6) y=x3-2 2.若幂函数y=f(x)的图象过点 ,则函数的解析式为__________ 练一练:3.已知 是幂函数,则m=________(1)(2)(4)x∈[0,+∞)课堂活动:
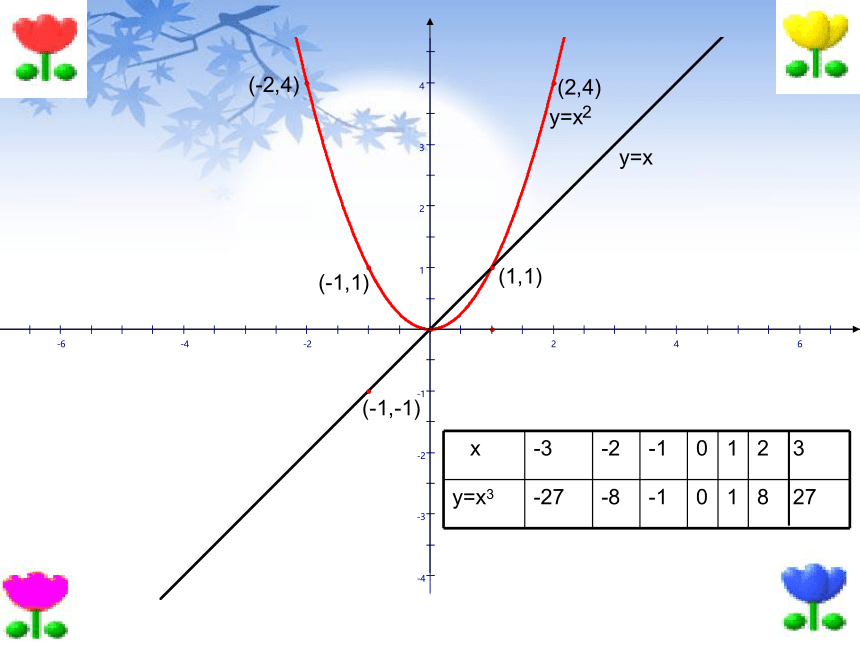
画出下列六个常见幂函数的图像(要求分组完成)1.画图的基本步骤:列表,描点,连线3.将六个函数图像画到一个直角坐标系中。
1. 与 y=1 的区别。2. 与 的画法。思考:2.从图像中读出函数的定义域,值域,奇偶性,单调性,公共点。完成书上78页的探究。3.同组间讨论总结幂函数的特征。注意:奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当α>0时,图象随x增大而上升。
当α<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?图象都经过点(1,1)α>0时,图象还都过点(0,0)点 (1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); (2) 如果α>0,则幂函数图象过原点,并且在区间[0,+∞)上是增函数; (3) 如果α<0,则幂函数图象在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x趋向于+∞时,图象在x轴上方无限地逼近x轴;(4) 当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.幂函数的性质 理论(5)所有的幂函数的图像都不过第四象限。a<0a>10的大致图像。yOy=x4y=x-3y=x-3合作探究:
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1检验:当 m=2时,函数为符合题意.当m=-1时,函数为不合题意,舍去.所以m=2偶函数变式探究变式探究2:
如果幂函数 的图像关于y轴对称,且在区间(0,+∞)内是减函数,则n的值为( )
A.-3 B.1
C.2 D.1或-3B例2 比较下列各组数的大小; 利用幂函数的增减性比较两个同
指数的数的大小。
当不能直接进行比较时,可在两个数
数中间插入一个中间数,间接比较这两
个数的大小。注意>><变式迁移 设a=0.20.3,b=0.30.3,c=0.30.2,则a,b,c的大小关系为 ( )
A.a>b>c B.aC.a解析:∵y=x0.3在(0,+∞)上是增函数且0.2<0.3,∴0.20.3<0.30.3,
又∵y=0.3x在R上是减函数且0.3>0.2,
∴0.30.3<0.30.2.
综上,知0.20.3<0.30.3<0.30.2,即a答案:B幂函数概念数形结合图象基本性质通过本节课的学习,你对幂函数有什么样的认识?能概括一下吗?作业:1.书上第82页第10题
2.根据幂函数的特征画出 和 的草图。总结他们的特征。谢 谢证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例3证明:任取所以幂函数 在[0,+∞)上是增函数.
问题1:如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p = 元, 。
问题2:如果正方形的边长为a,那么正方形的面积 是S = , 。
问题3:如果立方体的边长为a,那么立方体的体积是V = , 。
问题4:如果正方形场地的面积为S,那么正方形的边长a= , 。
问题5:如果某人t s内骑车行进了1km,那么他骑车的平均速度v = , 。 w这里p是w的函数a2这里S是a的函数a3这里V是a的函数这里a是S的函数这里v是t的函数若将它们的自变量全部用x来表示,函数值用y来表示,则它们的函数关系式将是:引入观察引入:观察下列五组函数总结他们的共同特征共同特征:
1.形如
2.都是以自变量x为底数;
3.指数为常数;
4.前面的系数为1;
5.只有一项。
比较幂函数与指数函数a为底数(a>0且a≠1)
指数底数幂值幂值判断一个函数是幂函数还是指数函数切入点 看自变量x是指数还是底数幂函数指数函数 1.下列函数是幂函数的是 ( ).(1) y=x4 (3) y= -x2 (5) y=3x2 (6) y=x3-2 2.若幂函数y=f(x)的图象过点 ,则函数的解析式为__________ 练一练:3.已知 是幂函数,则m=________(1)(2)(4)x∈[0,+∞)课堂活动:
画出下列六个常见幂函数的图像(要求分组完成)1.画图的基本步骤:列表,描点,连线3.将六个函数图像画到一个直角坐标系中。
1. 与 y=1 的区别。2. 与 的画法。思考:2.从图像中读出函数的定义域,值域,奇偶性,单调性,公共点。完成书上78页的探究。3.同组间讨论总结幂函数的特征。注意:奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当α>0时,图象随x增大而上升。
当α<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?图象都经过点(1,1)α>0时,图象还都过点(0,0)点 (1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); (2) 如果α>0,则幂函数图象过原点,并且在区间[0,+∞)上是增函数; (3) 如果α<0,则幂函数图象在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x趋向于+∞时,图象在x轴上方无限地逼近x轴;(4) 当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.幂函数的性质 理论(5)所有的幂函数的图像都不过第四象限。a<0a>10
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1检验:当 m=2时,函数为符合题意.当m=-1时,函数为不合题意,舍去.所以m=2偶函数变式探究变式探究2:
如果幂函数 的图像关于y轴对称,且在区间(0,+∞)内是减函数,则n的值为( )
A.-3 B.1
C.2 D.1或-3B例2 比较下列各组数的大小; 利用幂函数的增减性比较两个同
指数的数的大小。
当不能直接进行比较时,可在两个数
数中间插入一个中间数,间接比较这两
个数的大小。注意>><变式迁移 设a=0.20.3,b=0.30.3,c=0.30.2,则a,b,c的大小关系为 ( )
A.a>b>c B.a
又∵y=0.3x在R上是减函数且0.3>0.2,
∴0.30.3<0.30.2.
综上,知0.20.3<0.30.3<0.30.2,即a
2.根据幂函数的特征画出 和 的草图。总结他们的特征。谢 谢证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例3证明:任取所以幂函数 在[0,+∞)上是增函数.
