3.1.1 方程的根与函数的零点课件29张PPT
文档属性
| 名称 | 3.1.1 方程的根与函数的零点课件29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 549.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 00:00:00 | ||
图片预览






文档简介
课件29张PPT。人教版必修一
第三章
函数的应用课前热身:求下列方程的根方程的根
与
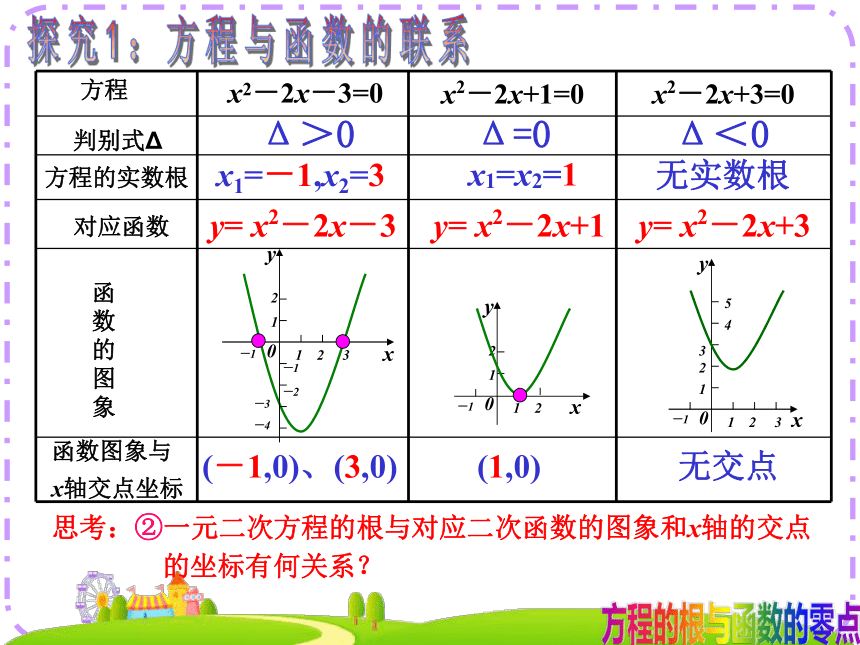
函数的零点探究1:方程与函数的联系方程x2-2x+1=0x2-2x+3=0对应函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x-3y= x2-2x+1y= x2-2x+3函数图象与
x轴交点坐标判别式ΔΔ>0Δ=0Δ<0思考:①一元二次方程不相等实数根的个数与对应二次函数的图
象和x轴交点个数有何关系? 探究1:方程与函数的联系方程x2-2x+1=0x2-2x+3=0对应函数函
数
的
图
象方程的实数根x1=-1,x2=3无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x-3y= x2-2x+1y= x2-2x+3函数图象与
x轴交点坐标判别式ΔΔ>0Δ=0Δ<0思考:②一元二次方程的根与对应二次函数的图象和x轴的交点
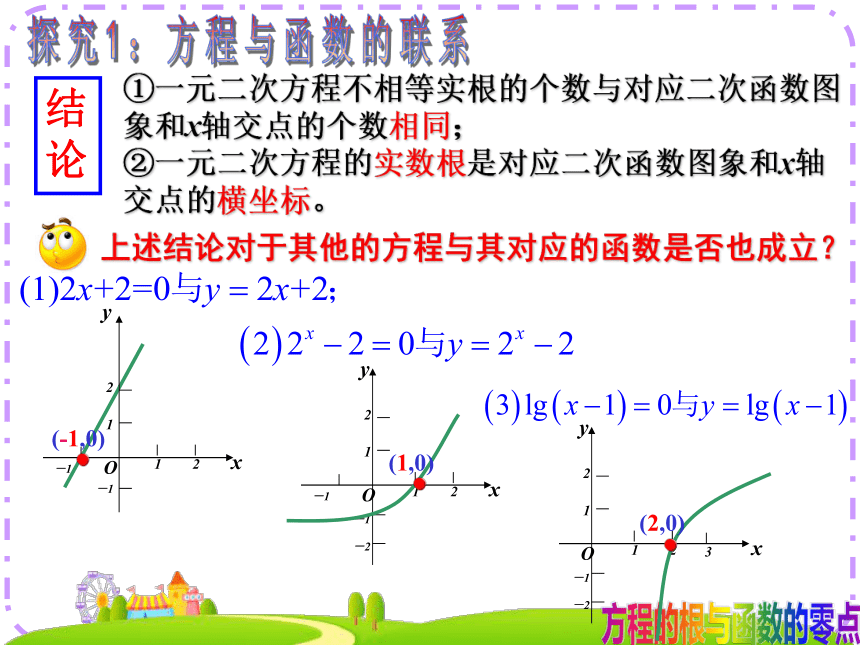
的坐标有何关系? x1=x2=1 上述结论对于其他的方程与其对应的函数是否也成立?探究1:方程与函数的联系①一元二次方程不相等实根的个数与对应二次函数图象和x轴交点的个数相同;
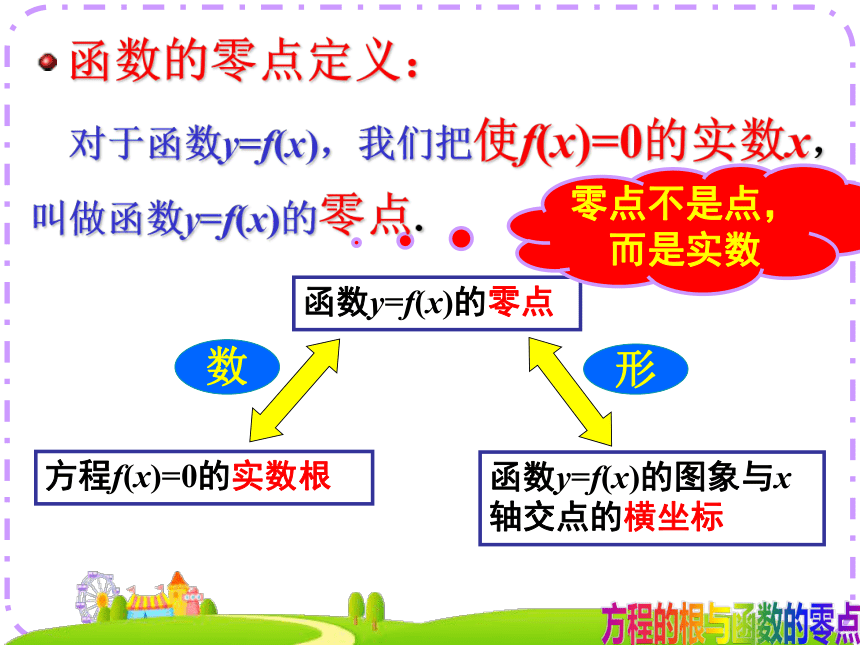
②一元二次方程的实数根是对应二次函数图象和x轴交点的横坐标。结论(-1,0)(1,0)(2,0)探究1:方程与函数的联系推广:交点为(x0,0)有交点交点的个数函数的零点定义:方程f(x)=0的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点形数零点不是点,而是实数 对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.函数的零点定义: 对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.方程f(x)=0的根代数法函数y=f(x)的图象与x轴交点的横坐标图象法等价关系:方程f(x)=0有实数根-2-123(1)下图中函数的零点有 练习一-2,-1,2和3AC-1和2练习一探究2:函数零点存在性问题 下图是某市1月份的某一天从0点到12点的气温变化图,假设气温是连续变化的,请将图形补充成完整的函数图象。思考:
这段时间内,是否一定有某一时刻的气温为0度?类比探究:
函数y=f(x)存在零点的条件是什么? 假设函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,请画出下列三种情况下经过A、B两点的可能的函数图象。ab x ab x猜想:
函数y=f(x)的图象在区间[a,b]上连续,如果有 ,那么函数在区间(a,b)上有零点.f(a) f(b)<0探究2:函数零点存在性问题ABABab xAB一定存在零点不一定存在零点不一定存在零点AB函数零点存在性定理: 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。 即存在 c∈(a,b) 即存在 c∈(a,b) ,使得 f(c) =0,这个c也就是方程 f(x)=0 的根。(1)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b)<0,则 f(x)在区间(a,b)内有且仅有一个零点。 ( )(2)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b) ≥0,则f(x)在区间(a,b)内没有零点。 ( )(3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。 ( )×××(4)已知函数y=f(x)在区间[a,b]上图象是连续的,且存在零点,则f(a)f(b)<0 。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理不能确定零点的个数 (1)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b)<0,则 f(x)在区间(a,b)内有且仅有一个零点。( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:不满足定理条件时依然可能有零点存在 (2)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b) ≥0,则f(x)在区间(a,b)内没有零点。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理中的“连续不断”是必不可少的 (3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理反之不成立 (4)已知函数y=f(x)在区间[a,b]上图象是连续的,且存在零点,则f(a)f(b)<0 。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理不能确定零点的个数;
不满足定理条件时依然可能有零点;
定理中的“连续不断”是必不可少的条件;
定理反之不成立。 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。函数零点存在性定理:例2 函数 f(x)=lnx+2x-6 在下列哪个区间有零点A.(0,1) B.(1,2) C.(2,3) D.(3,4)C例1 已知函数 的图象是连续不断的一条曲线,
且有如下对应值表,则函数在哪些区间内有零点?典例分析:函数存在零点函数图象连续区间端点处函数值异号利用函数零点存在性定理判断零点所在区间的步骤(1) 确定函数y=f(x)在[a, b]上图象连续;(2) 通过计算判断f(a)、f(b)的符号(3) 若f(a)·f(b)<0, 则函数y=f(x)在(a, b)内存在零点.方法小结:学以致用C(2)函数f(x)=x3+x-1在下列哪个区间有零点( ) A.(-1,0) B.(0,1) C.(1,2) D.(2,3)BC函数的零点数形结合函数与方程化归与转化是数,
不是点函数零点存在性定理函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续方可行。课后作业:
1、课本P88,练习1;P92,A组2;P112,A组1
2、思考:
如何求出f(x)=lnx+2x-6的零点?变式 已知函数 ,试借助计算机,确定它有几个零点及零点所在区间(n,n+1)(n∈Z)。解 :用计算机做出x、f(x)对应值表和图象如下: 由表和图象可知,f(2)<0,f(3)>0,f(2)f(3)<0,这说明函数f(x)在区间(2,3)内有零点。思考:可否判定零点的个数? 因为函数f(x)在(0,+∞)内单调递增,所以它仅有一个零点.解法二 :确定函数f(x)=lnx+2x-6零点的个数y=lnxy=-2x+6 由图可知,两函数图象只有一个交点,即方程只有一根,并且根在区间(2,3)内。变式 已知函数 ,试借助计算机,确定它有几个零点及零点所在区间(n,n+1)(n∈Z)。函数的零点数形结合函数与方程化归与转化是数,
不是点函数零点存在性定理函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续方可行。课后作业:
1、课本P88,练习1;P92,A组2;P112,A组1
2、思考:
如何求出f(x)=lnx+2x-6的零点?
第三章
函数的应用课前热身:求下列方程的根方程的根
与
函数的零点探究1:方程与函数的联系方程x2-2x+1=0x2-2x+3=0对应函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x-3y= x2-2x+1y= x2-2x+3函数图象与
x轴交点坐标判别式ΔΔ>0Δ=0Δ<0思考:①一元二次方程不相等实数根的个数与对应二次函数的图
象和x轴交点个数有何关系? 探究1:方程与函数的联系方程x2-2x+1=0x2-2x+3=0对应函数函
数
的
图
象方程的实数根x1=-1,x2=3无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x-3y= x2-2x+1y= x2-2x+3函数图象与
x轴交点坐标判别式ΔΔ>0Δ=0Δ<0思考:②一元二次方程的根与对应二次函数的图象和x轴的交点
的坐标有何关系? x1=x2=1 上述结论对于其他的方程与其对应的函数是否也成立?探究1:方程与函数的联系①一元二次方程不相等实根的个数与对应二次函数图象和x轴交点的个数相同;
②一元二次方程的实数根是对应二次函数图象和x轴交点的横坐标。结论(-1,0)(1,0)(2,0)探究1:方程与函数的联系推广:交点为(x0,0)有交点交点的个数函数的零点定义:方程f(x)=0的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点形数零点不是点,而是实数 对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.函数的零点定义: 对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.方程f(x)=0的根代数法函数y=f(x)的图象与x轴交点的横坐标图象法等价关系:方程f(x)=0有实数根-2-123(1)下图中函数的零点有 练习一-2,-1,2和3AC-1和2练习一探究2:函数零点存在性问题 下图是某市1月份的某一天从0点到12点的气温变化图,假设气温是连续变化的,请将图形补充成完整的函数图象。思考:
这段时间内,是否一定有某一时刻的气温为0度?类比探究:
函数y=f(x)存在零点的条件是什么? 假设函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,请画出下列三种情况下经过A、B两点的可能的函数图象。ab x ab x猜想:
函数y=f(x)的图象在区间[a,b]上连续,如果有 ,那么函数在区间(a,b)上有零点.f(a) f(b)<0探究2:函数零点存在性问题ABABab xAB一定存在零点不一定存在零点不一定存在零点AB函数零点存在性定理: 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。 即存在 c∈(a,b) 即存在 c∈(a,b) ,使得 f(c) =0,这个c也就是方程 f(x)=0 的根。(1)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b)<0,则 f(x)在区间(a,b)内有且仅有一个零点。 ( )(2)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b) ≥0,则f(x)在区间(a,b)内没有零点。 ( )(3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。 ( )×××(4)已知函数y=f(x)在区间[a,b]上图象是连续的,且存在零点,则f(a)f(b)<0 。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理不能确定零点的个数 (1)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b)<0,则 f(x)在区间(a,b)内有且仅有一个零点。( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:不满足定理条件时依然可能有零点存在 (2)已知函数y=f(x)在区间[a,b]上图象是连续的,且f(a)f(b) ≥0,则f(x)在区间(a,b)内没有零点。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理中的“连续不断”是必不可少的 (3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理反之不成立 (4)已知函数y=f(x)在区间[a,b]上图象是连续的,且存在零点,则f(a)f(b)<0 。 ( )× 练习二:判断下列结论是否正确,若不正确,请画出相应函数图象加以说明。 结论:定理不能确定零点的个数;
不满足定理条件时依然可能有零点;
定理中的“连续不断”是必不可少的条件;
定理反之不成立。 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。函数零点存在性定理:例2 函数 f(x)=lnx+2x-6 在下列哪个区间有零点A.(0,1) B.(1,2) C.(2,3) D.(3,4)C例1 已知函数 的图象是连续不断的一条曲线,
且有如下对应值表,则函数在哪些区间内有零点?典例分析:函数存在零点函数图象连续区间端点处函数值异号利用函数零点存在性定理判断零点所在区间的步骤(1) 确定函数y=f(x)在[a, b]上图象连续;(2) 通过计算判断f(a)、f(b)的符号(3) 若f(a)·f(b)<0, 则函数y=f(x)在(a, b)内存在零点.方法小结:学以致用C(2)函数f(x)=x3+x-1在下列哪个区间有零点( ) A.(-1,0) B.(0,1) C.(1,2) D.(2,3)BC函数的零点数形结合函数与方程化归与转化是数,
不是点函数零点存在性定理函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续方可行。课后作业:
1、课本P88,练习1;P92,A组2;P112,A组1
2、思考:
如何求出f(x)=lnx+2x-6的零点?变式 已知函数 ,试借助计算机,确定它有几个零点及零点所在区间(n,n+1)(n∈Z)。解 :用计算机做出x、f(x)对应值表和图象如下: 由表和图象可知,f(2)<0,f(3)>0,f(2)f(3)<0,这说明函数f(x)在区间(2,3)内有零点。思考:可否判定零点的个数? 因为函数f(x)在(0,+∞)内单调递增,所以它仅有一个零点.解法二 :确定函数f(x)=lnx+2x-6零点的个数y=lnxy=-2x+6 由图可知,两函数图象只有一个交点,即方程只有一根,并且根在区间(2,3)内。变式 已知函数 ,试借助计算机,确定它有几个零点及零点所在区间(n,n+1)(n∈Z)。函数的零点数形结合函数与方程化归与转化是数,
不是点函数零点存在性定理函数零点方程根,
形数本是同根生。
函数零点端点判,
图象连续方可行。课后作业:
1、课本P88,练习1;P92,A组2;P112,A组1
2、思考:
如何求出f(x)=lnx+2x-6的零点?
