人教版八年级上册11.1.1 三角形的边课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册11.1.1 三角形的边课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-30 00:05:52 | ||
图片预览


文档简介
(共18张PPT)
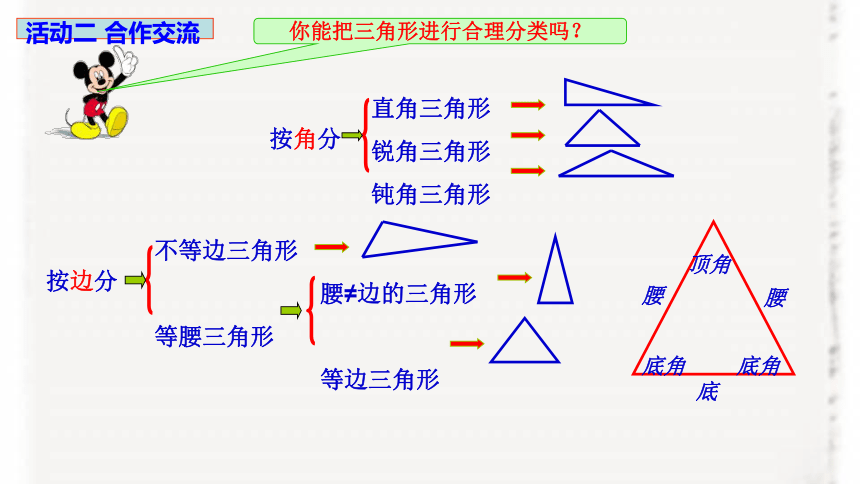
与三角形有关的线段
第一课时 三角形的边
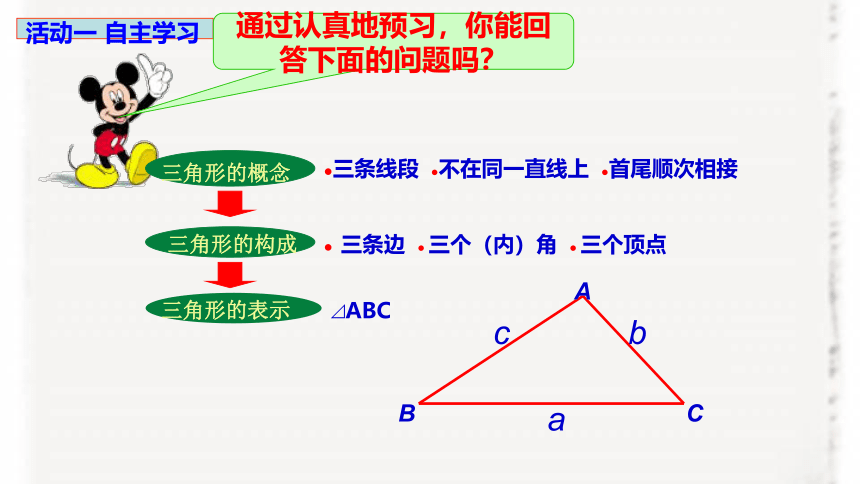
通过认真地预习,你能回答下面的问题吗?
●三条线段 ●不在同一直线上 ●首尾顺次相接
● 三条边 ● 三个(内)角 ● 三个顶点
⊿ABC
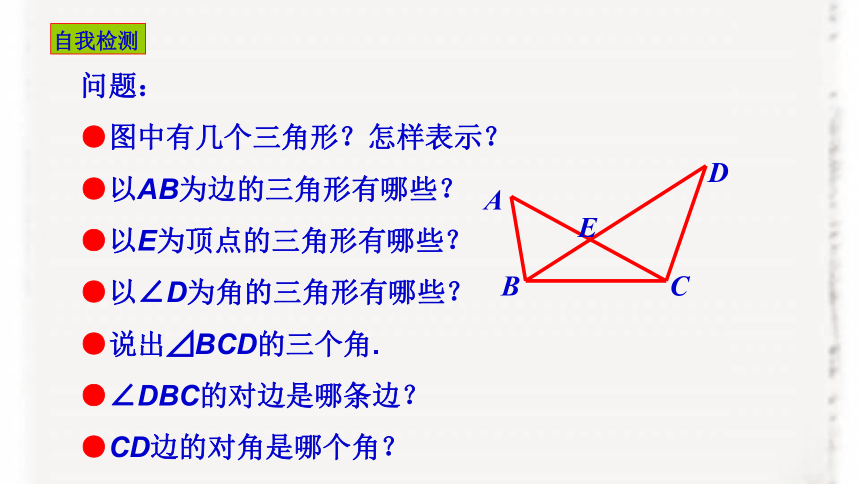
问题:
●图中有几个三角形?怎样表示?
●以AB为边的三角形有哪些?
●以E为顶点的三角形有哪些?
●以∠D为角的三角形有哪些?
●说出⊿BCD的三个角.
●∠DBC的对边是哪条边?
●CD边的对角是哪个角?
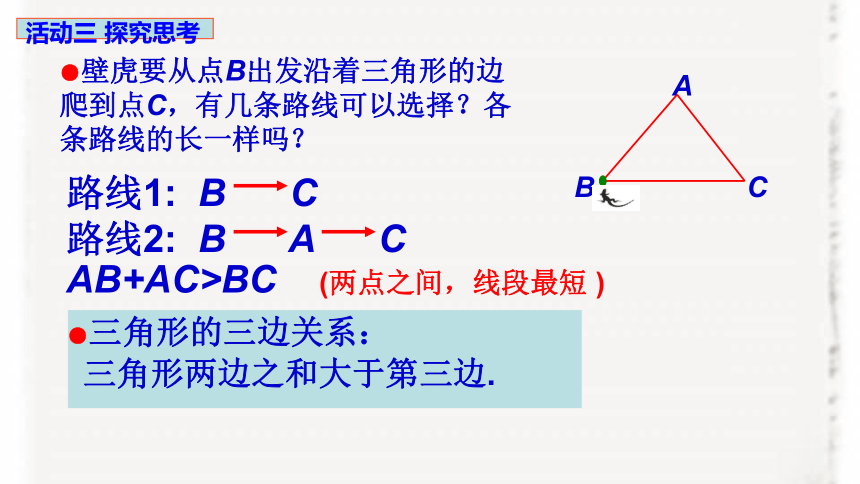
●壁虎要从点B出发沿着三角形的边爬到点C,有几条路线可以选择?各条路线的长一样吗?
AB+AC>BC (两点之间,线段最短 )
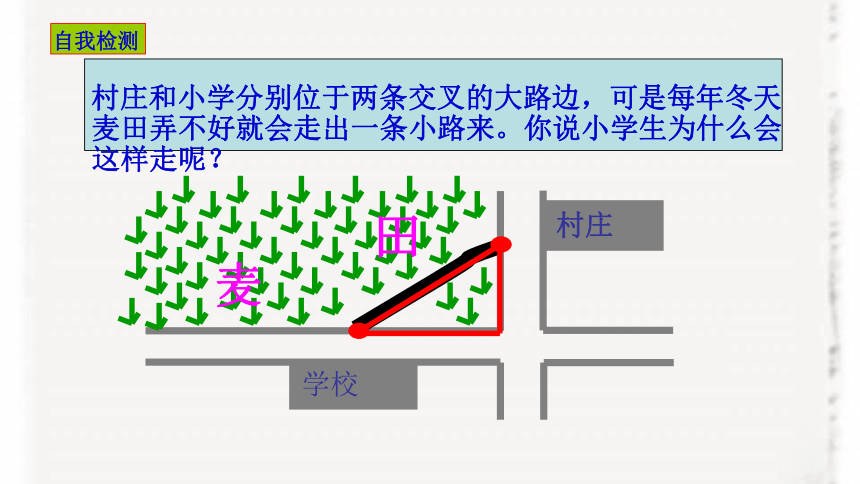
村庄和小学分别位于两条交叉的大路边,可是每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
例1:下列长度的三条线段能否组成三角形?为什么?
① 3 , 4, 8 ② 5 , 6 , 11 ③ 5 , 6, 10
解:①不能,因为3+4<8,即两条线段的和小于第三条线段.
③能,因为任意两条线段的和都大于第三条线段.
②不能,因为5+6=11,即两条线段的和等于第三条直线.
练习:下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
小巧门: 用较短的两条线段之和与最长的线段比较,若和大,能组成三 角形,反之,则不能。
思 考:在一个三角形中,任意两边之差与第三边有什么关系?
a
b
c
在三角形中,任意两边之差小于第三边
结 论:
如右图:在ABC中,
a-b<c
b-c<a
c-a<b
注意:
1、一个三角形的三边关系可以归纳成如下一句话:
三角形的任意两边之和大于第三边,任意两边之差小于第三边。
2、在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边。
例2:若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。
注意:
1、一个三角形的三边关系可以归纳成如下一句话:
三角形的任意两边之和大于第三边,任意两边之差小于 第三边。
2、在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边。
设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
解:
答:第三边的长为7。
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,解得x=7.
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,解得x=10,
∵4+4﹤10
∴此时构不成三角形
解:①设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18
解得x=3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米。
(1)已知等腰三角形的一边等于7,一边等
于8,则它的周长为 .
(2)已知等腰三角形的一边等于6,一边等
于13,则它的周长为 .
22或23
32
课堂练习:
1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒
2.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cm
一、选择题:
B
C
B
二、填空题:
5.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形。
6.若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为 。
7.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________。
3
17
10或11
25cm
三、解答题:
8、用一根长为28厘米的细铁丝围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为7厘米的等腰三角形吗?为什么?
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
与三角形有关的线段
第一课时 三角形的边
通过认真地预习,你能回答下面的问题吗?
●三条线段 ●不在同一直线上 ●首尾顺次相接
● 三条边 ● 三个(内)角 ● 三个顶点
⊿ABC
问题:
●图中有几个三角形?怎样表示?
●以AB为边的三角形有哪些?
●以E为顶点的三角形有哪些?
●以∠D为角的三角形有哪些?
●说出⊿BCD的三个角.
●∠DBC的对边是哪条边?
●CD边的对角是哪个角?
●壁虎要从点B出发沿着三角形的边爬到点C,有几条路线可以选择?各条路线的长一样吗?
AB+AC>BC (两点之间,线段最短 )
村庄和小学分别位于两条交叉的大路边,可是每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
例1:下列长度的三条线段能否组成三角形?为什么?
① 3 , 4, 8 ② 5 , 6 , 11 ③ 5 , 6, 10
解:①不能,因为3+4<8,即两条线段的和小于第三条线段.
③能,因为任意两条线段的和都大于第三条线段.
②不能,因为5+6=11,即两条线段的和等于第三条直线.
练习:下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
小巧门: 用较短的两条线段之和与最长的线段比较,若和大,能组成三 角形,反之,则不能。
思 考:在一个三角形中,任意两边之差与第三边有什么关系?
a
b
c
在三角形中,任意两边之差小于第三边
结 论:
如右图:在ABC中,
a-b<c
b-c<a
c-a<b
注意:
1、一个三角形的三边关系可以归纳成如下一句话:
三角形的任意两边之和大于第三边,任意两边之差小于第三边。
2、在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边。
例2:若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长。
注意:
1、一个三角形的三边关系可以归纳成如下一句话:
三角形的任意两边之和大于第三边,任意两边之差小于 第三边。
2、在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边。
设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
解:
答:第三边的长为7。
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,解得x=7.
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,解得x=10,
∵4+4﹤10
∴此时构不成三角形
解:①设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18
解得x=3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米。
(1)已知等腰三角形的一边等于7,一边等
于8,则它的周长为 .
(2)已知等腰三角形的一边等于6,一边等
于13,则它的周长为 .
22或23
32
课堂练习:
1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( )
A.10cm的木棒 B.20cm的木棒 C.50cm的木棒 D.60cm的木棒
2.已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )
A.2cm B.3cm C.4cm D.5cm
一、选择题:
B
C
B
二、填空题:
5.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形。
6.若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为 。
7.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________。
3
17
10或11
25cm
三、解答题:
8、用一根长为28厘米的细铁丝围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为7厘米的等腰三角形吗?为什么?
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
A
D
C
B
H
H′
