人教版选修2-3 2.4正态分布课件(25张)
文档属性
| 名称 | 人教版选修2-3 2.4正态分布课件(25张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 23:42:51 | ||
图片预览






文档简介
课件25张PPT。2.4 正态分布高二数学 选修2-3随机变量离散型随机变量连续型随机变量特点:取值具有可列性特点:取某个区间内的一切值 三种常见的离散型分布:
两点分布、超几何分布
二项分布复习连续型随机变量是否也存在分布?
统计案例: 从一批产品中抽取容量为100的样本,尺寸数据表示如下(单位:mm): 25.41 25.43 25.25 25.54 25.75 25.84 25.32 25.80 25.65 25.24 25.67 25.33 25.48 25.86 25.63 25.27 25.40 25.55 25.87 25.23 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.70 25.66 25.87 25.27 25.46 25.79 25.49 25.63 25.41 25.43 25.25 25.54 25.78 25.86 25.32 25.81 25.68 25.29 25.60 25.34 25.47 25.88 25.69 25.29 25.41 25.59 25.24 25.27 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.70 25.66 25.87 25.27 25.46 25.79 25.49 25.63 25.48 25.86 25.63 25.84 25.43 25.58 25.82 25.29 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.74 25.67 25.89 25.24 25.57 25.58 25.62 25.27 25.72 25.63 25. 85 25.28
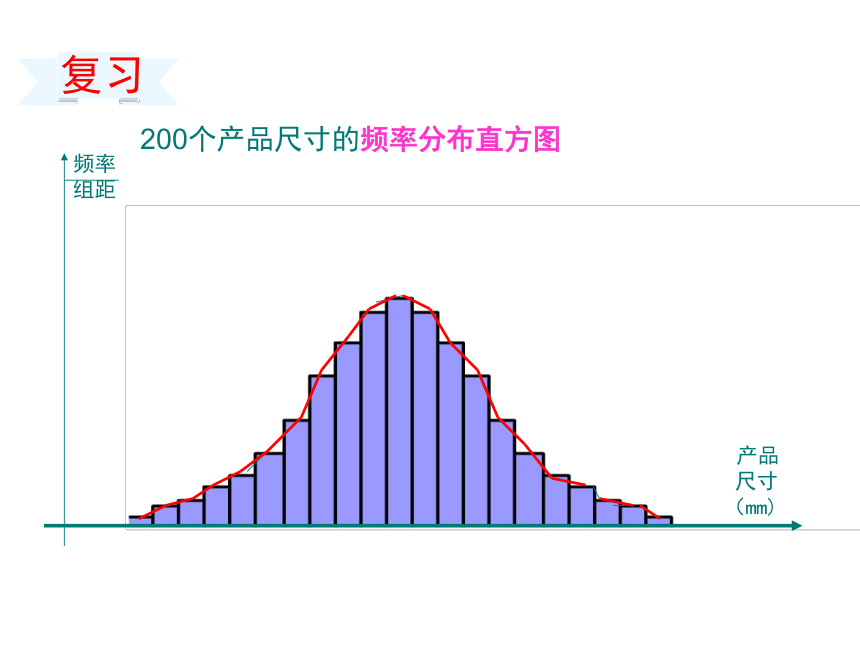
复习100个产品尺寸的频率分布直方图25.2325.2925.3525.4125.4725.53 产品
尺寸
(mm)频率/组距25.6525.5925.7125.7725.8325.89复习200个产品尺寸的频率分布直方图 产品
尺寸
(mm)频率
组距
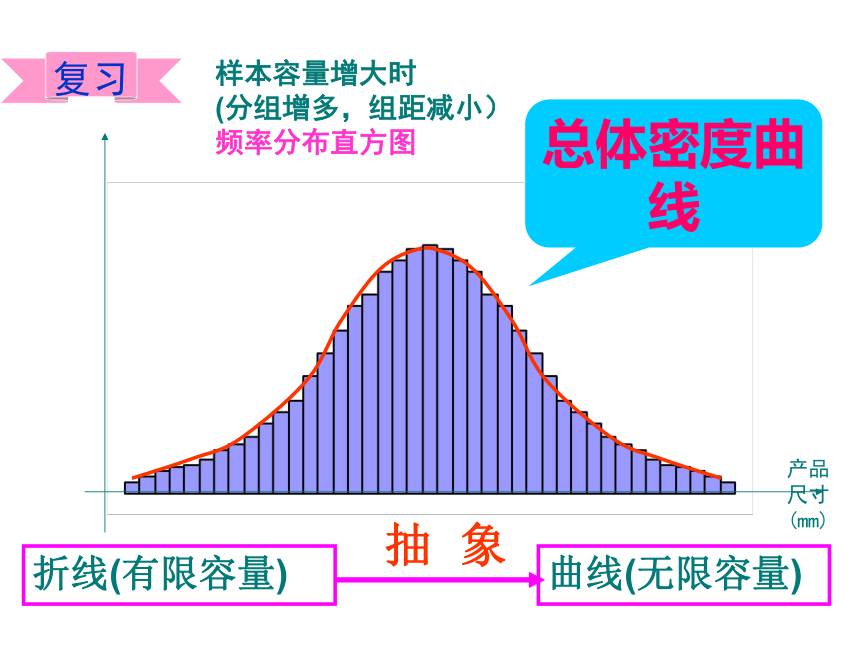
复习样本容量增大时
(分组增多,组距减小)
频率分布直方图频率
组距产品
尺寸
(mm)总体密度曲线抽 象一起来探究1、总体密度曲线为什么呈现“中间高、 两头低”的分布特点?
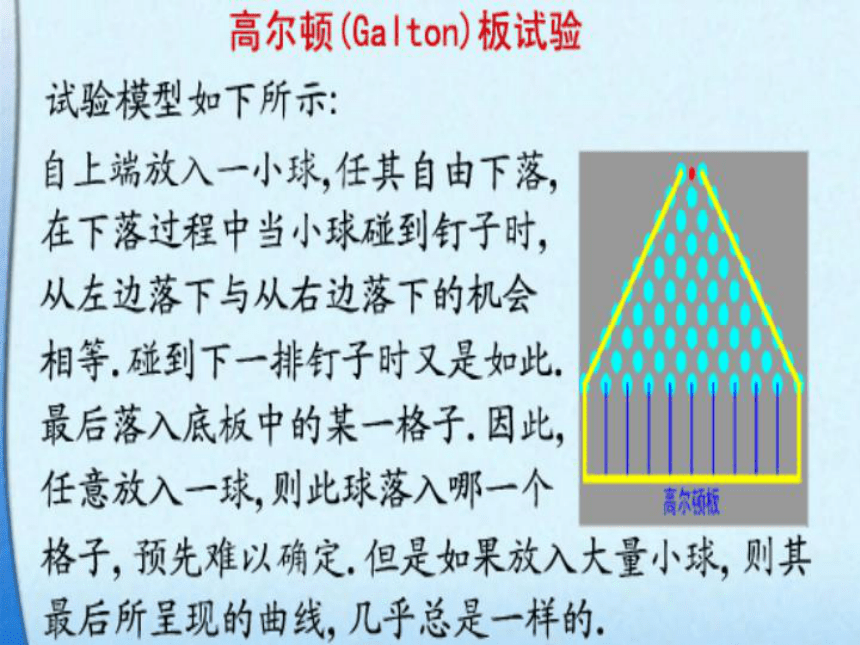
2、该曲线能不能和横轴相交?原因是什么?高尔顿板演示11频率/组距钟形曲线0想一想,这条曲线和以前学过的哪些函数图象相似?导入在大量重复试验下,高尔顿板试验得到的曲线图就是或近似地是以下函数的图象:函数这就是正态密度函数 m 的意义x总体平均数反映总体随机变量取值的 平均水平x3x4χ=μyxχ=μy总体标准差反映总体随机变量的 集中与分散的程度 s的意义想一想,如何验证对称问题.μ正态密度函数表达式012-1-2xy-3x=μ(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 正态曲线性质具有两头低、中间高、左右对称的基本特征小试牛刀练习:若一个正态分布的密度函数是一个偶函数且该函数的最大值等于 ,求该正态分布的密度函数解析式。标准差相等、平均数不等的正态分布图示σ=0.5μ= -1μ=0 μ= 1平均数相等、标准差不等的正态分布图示?=0?=1若 固定, 越大时, 曲线越矮胖;
越小, 曲线越瘦高, 故称
为形状参数。?=2(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近. 3、正态曲线的性质例3、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为密度曲线的总体的平均值比以曲线a为密度曲线的总体的平均值大2;
D.以曲线b为密度曲线的总体的方差比以曲线a为密度曲线的总体的方差大2。D正态曲线下的面积规律X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。S(-?,-X)S(X,+?)=S(-?,-X)?正态曲线下的面积规律对称区域面积相等。S(-x1, -x2)-x1 -x2 x2 x1S(x1,x2)=S(-x2,-x1)?例4、在某次数学考试中,考生的成绩 服从一个正态分布,即 ~N(90,100).
(1)试求考试成绩 位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?C2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则 = ,
= .
4、若X~N(5,1),求P(6
两点分布、超几何分布
二项分布复习连续型随机变量是否也存在分布?
统计案例: 从一批产品中抽取容量为100的样本,尺寸数据表示如下(单位:mm): 25.41 25.43 25.25 25.54 25.75 25.84 25.32 25.80 25.65 25.24 25.67 25.33 25.48 25.86 25.63 25.27 25.40 25.55 25.87 25.23 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.70 25.66 25.87 25.27 25.46 25.79 25.49 25.63 25.41 25.43 25.25 25.54 25.78 25.86 25.32 25.81 25.68 25.29 25.60 25.34 25.47 25.88 25.69 25.29 25.41 25.59 25.24 25.27 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.70 25.66 25.87 25.27 25.46 25.79 25.49 25.63 25.48 25.86 25.63 25.84 25.43 25.58 25.82 25.29 25.45 25.53 25.68 25.77 25.50 25.56 25.64 25.24 25.74 25.67 25.89 25.24 25.57 25.58 25.62 25.27 25.72 25.63 25. 85 25.28
复习100个产品尺寸的频率分布直方图25.2325.2925.3525.4125.4725.53 产品
尺寸
(mm)频率/组距25.6525.5925.7125.7725.8325.89复习200个产品尺寸的频率分布直方图 产品
尺寸
(mm)频率
组距
复习样本容量增大时
(分组增多,组距减小)
频率分布直方图频率
组距产品
尺寸
(mm)总体密度曲线抽 象一起来探究1、总体密度曲线为什么呈现“中间高、 两头低”的分布特点?
2、该曲线能不能和横轴相交?原因是什么?高尔顿板演示11频率/组距钟形曲线0想一想,这条曲线和以前学过的哪些函数图象相似?导入在大量重复试验下,高尔顿板试验得到的曲线图就是或近似地是以下函数的图象:函数这就是正态密度函数 m 的意义x总体平均数反映总体随机变量取值的 平均水平x3x4χ=μyxχ=μy总体标准差反映总体随机变量的 集中与分散的程度 s的意义想一想,如何验证对称问题.μ正态密度函数表达式012-1-2xy-3x=μ(1)曲线在x轴的上方,与x轴不相交.(2)曲线是单峰的,它关于直线x=μ对称. 正态曲线性质具有两头低、中间高、左右对称的基本特征小试牛刀练习:若一个正态分布的密度函数是一个偶函数且该函数的最大值等于 ,求该正态分布的密度函数解析式。标准差相等、平均数不等的正态分布图示σ=0.5μ= -1μ=0 μ= 1平均数相等、标准差不等的正态分布图示?=0?=1若 固定, 越大时, 曲线越矮胖;
越小, 曲线越瘦高, 故称
为形状参数。?=2(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近. 3、正态曲线的性质例3、把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b。下列说法中不正确的是( )
A.曲线b仍然是正态曲线;
B.曲线a和曲线b的最高点的纵坐标相等;
C.以曲线b为密度曲线的总体的平均值比以曲线a为密度曲线的总体的平均值大2;
D.以曲线b为密度曲线的总体的方差比以曲线a为密度曲线的总体的方差大2。D正态曲线下的面积规律X轴与正态曲线所夹面积恒等于1 。
对称区域面积相等。S(-?,-X)S(X,+?)=S(-?,-X)?正态曲线下的面积规律对称区域面积相等。S(-x1, -x2)-x1 -x2 x2 x1S(x1,x2)=S(-x2,-x1)?例4、在某次数学考试中,考生的成绩 服从一个正态分布,即 ~N(90,100).
(1)试求考试成绩 位于区间(70,110)上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?C2、已知X~N (0,1),则X在区间 内取值的概率等于( )
A.0.9544 B.0.0456 C.0.9772 D.0.0228
3、设离散型随机变量X~N(0,1),则 = ,
= .
4、若X~N(5,1),求P(6
