高中数学新人教A版必修1课件:第二章基本初等函数2.1.2指数函数及其性质(第1课时)指数函数及其性质(33张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第二章基本初等函数2.1.2指数函数及其性质(第1课时)指数函数及其性质(33张) |  | |
| 格式 | zip | ||
| 文件大小 | 780.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:11:58 | ||
图片预览










文档简介
课件33张PPT。第二章基本初等函数(Ⅰ)2.1 指数函数2.1.2 指数函数及其性质第一课时 指数函数及其性质自主预习学案2010年11月1日,全国人口普查全面展开,而2000年我国约有13亿人口.我国政府现在实行计划生育政策,人口年增长率较低.若按年增长率1%计算,到2010年底,我国人口将增加多少?到2020年底,我国人口总数将达到多少?如果我们放开计划生育政策,年增长率是2%,甚至是5%,那么结果将会是怎样的呢?会带来灾难性后果吗?1.指数函数的定义
一般地,函数y=______(a>0,且a≠1)叫做指数函数,其中x是__________.
[知识点拨] 指数函数y=ax(a>0,且a≠1)的结构特征:
(1)底数:大于零且不等于1的常数;
(2)指数:仅有自变量x;
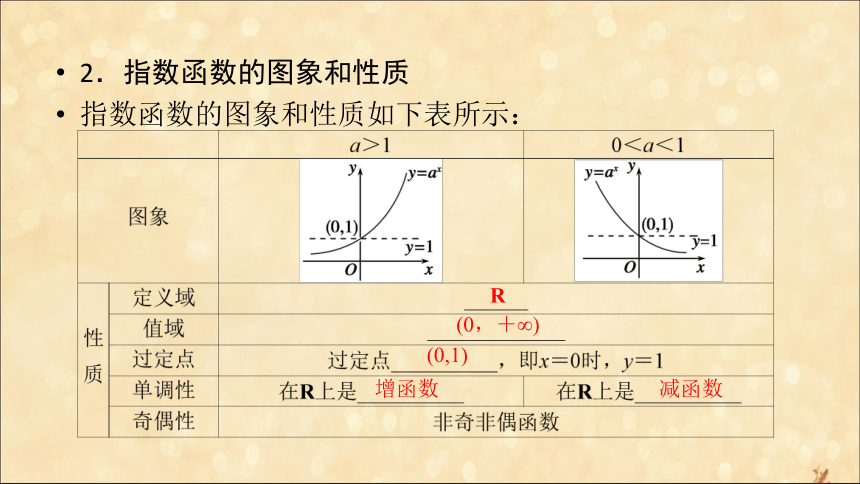
(3)系数:ax的系数是1.ax 自变量 2.指数函数的图象和性质
指数函数的图象和性质如下表所示:R (0,+∞) (0,1) 增函数 减函数
[知识点拨] (1)a>1是“一撇”,0(2)图象位于x轴上方;
(3)当x=0时,y=1;
(4)在y轴右侧,a越大,图象越高,即逆时针方向,底数依次增大.1.下列函数中一定是指数函数的是 ( )
A.y=2x+1 B.y=x2
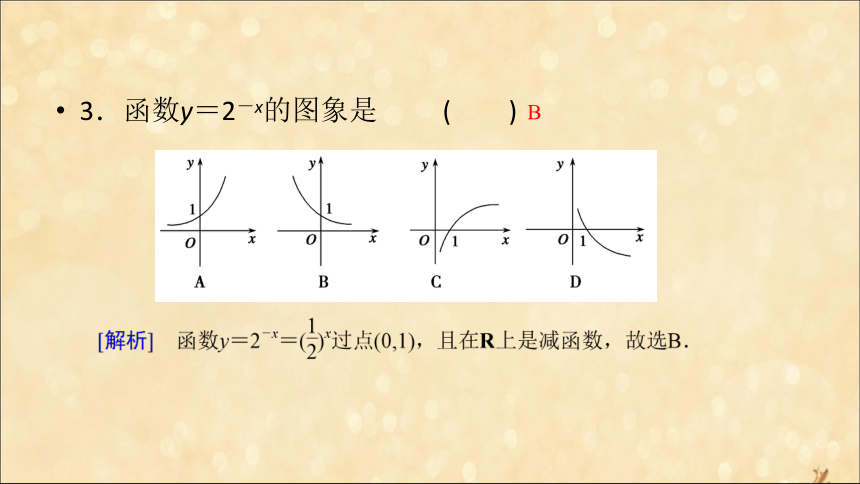
C.y=3-x D.y=-2·3xC D 3.函数y=2-x的图象是 ( )B
4.(2019·吉林乾安七中高一期中测试)指数函数f(x)的图象经过点(2,4),则f(3)=_____.
[解析] 设f(x)=ax(a>0且a≠1),
由题意,得4=a2,∴a=2.
∴f(x)=2x,∴f(3)=23=8.
8 5.若函数y=(k+2)ax+2-b(a>0,且a≠1)是指数函数,则k=_______,b=_____.-1 2 互动探究学案命题方向1 ?指数函数的概念 (1)下列以x为自变量的函数中,是指数函数的是 ( )
A.y=(-4)x B.y=πx
C.y=-4x D.y=ax+2(a>0,a≠1)
(2)若y=(a2-3a+3)ax是指数函数,则有 ( )
A.a=1或2 B.a=1
C.a=2 D.a>0且a≠1
[思路分析] 利用指数函数的定义进行判断.B 典例 1 C 『规律方法』 判断一个函数是否是指数函数,关键是看解析式是否符合y=ax(a>0,a≠1)这一结构形式.D 命题方向2 ?指数函数的图象 如图所示是下列指数函数的图象:
(1)y=ax;(2)y=bx;(3)y=cx;(4)y=dx.
则a,b,c,d与1的大小关系是 ( )
A.aB.bC.1D.a[思路分析] 根据指数函数的底数与图象间的关系来进行判断.
[解析] 可先分为两类,(3)(4)的底数一定大于1,(1)(2)的底数一定小于1,然后再由(3)(4)比较,c,d的大小,由(1)(2)比较a,b的大小.当指数函数的底数大于1时,图象上升,且当底数越大,图象向上越靠近y轴;当底数大于0小于1时,图象下降,且当底数越小,图象向下越靠近x轴,故选B.
『规律方法』 指数函数图象的变化规律
指数函数的图象随底数变化的规律可归纳为:在第一象限内,图象自下而上对应的底数依次增大.D [解析] 按规律,C1,C2,C3,C4的底数a依次增大,故选D.(2)若函数y=ax+(b-1)(a>0,且a≠1)的图象不经过第二象限,则有 ( )
A.a>1且b<1 B.0<a<1且b≤1
C.0<a<1且b>0 D.a>1且b≤0
[解析] 由函数图象不过第二象限知a>1,且x=0时,a0+(b-1)≤0,∴b≤0,故选D.D 指数函数中忽视对底数的分类讨论致误典例 5转化与化归思想的应用指数型函数的定义域、值域、图象与性质的讨论都可以化归为基本函数y=ax(a>0且a≠1)的相关知识来解决.[思路分析] (1)题中x-4满足什么条件时,函数有意义?y的值不可能取得什么?
(2)题中式子的指数中含有根式,若要有意义,需满足什么条件?典例 4『规律方法』 1.函数单调性在求函数值域中的应用
(1)若函数f(x)在区间[a,b]上是增函数,则f(a)≤f(x)≤f(b),值域为[f(a),f(b)].
(2)若函数f(x)在区间[a,b]上是减函数,则f(a)≥f(x)≥f(b),值域为[f(b),f(a)].
2.函数y=af(x)定义域、值域的求法
(1)定义域.
函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)值域.
①换元,令t=f(x);②求t=f(x)的定义域x∈D;③求t=f(x)的值域t∈M;④利用y=at的单调性求y=at,t∈M的值域.[解析] 根据指数函数的定义:形如y=ax(a>0,且a≠1)的函数叫做指数函数,结合选项从而可知y=52x=25x为指数函数,故选D.D
2.已知1>n>m>0,则指数函数①y=mx,②y=nx的图象为 ( )
[解析] 由于0<m<n<1,所以y=mx与y=nx都是减函数,故排除A、B项,作直线x=1与两个曲线相交,交点在下面的是函数y=mx的图象,故选C.C 3.(2019·安徽合肥众兴中学高一期末测试)函数y=ax-2+1(a>0且a≠1)的图象必经过点 ( )
A.(0,1) B.(1,1)
C.(2,0) D.(2,2)
[解析] 令x-2=0,即x=2,y=a0+1=2,故选D.D
5.函数y=2x(x≥0)的值域是______________.
[解析] ∵y=2x在[0,+∞)上为增函数,
∴x≥0即y≥20,
∴值域为[1,+∞).[1,+∞)
一般地,函数y=______(a>0,且a≠1)叫做指数函数,其中x是__________.
[知识点拨] 指数函数y=ax(a>0,且a≠1)的结构特征:
(1)底数:大于零且不等于1的常数;
(2)指数:仅有自变量x;
(3)系数:ax的系数是1.ax 自变量 2.指数函数的图象和性质
指数函数的图象和性质如下表所示:R (0,+∞) (0,1) 增函数 减函数
[知识点拨] (1)a>1是“一撇”,0
(3)当x=0时,y=1;
(4)在y轴右侧,a越大,图象越高,即逆时针方向,底数依次增大.1.下列函数中一定是指数函数的是 ( )
A.y=2x+1 B.y=x2
C.y=3-x D.y=-2·3xC D 3.函数y=2-x的图象是 ( )B
4.(2019·吉林乾安七中高一期中测试)指数函数f(x)的图象经过点(2,4),则f(3)=_____.
[解析] 设f(x)=ax(a>0且a≠1),
由题意,得4=a2,∴a=2.
∴f(x)=2x,∴f(3)=23=8.
8 5.若函数y=(k+2)ax+2-b(a>0,且a≠1)是指数函数,则k=_______,b=_____.-1 2 互动探究学案命题方向1 ?指数函数的概念 (1)下列以x为自变量的函数中,是指数函数的是 ( )
A.y=(-4)x B.y=πx
C.y=-4x D.y=ax+2(a>0,a≠1)
(2)若y=(a2-3a+3)ax是指数函数,则有 ( )
A.a=1或2 B.a=1
C.a=2 D.a>0且a≠1
[思路分析] 利用指数函数的定义进行判断.B 典例 1 C 『规律方法』 判断一个函数是否是指数函数,关键是看解析式是否符合y=ax(a>0,a≠1)这一结构形式.D 命题方向2 ?指数函数的图象 如图所示是下列指数函数的图象:
(1)y=ax;(2)y=bx;(3)y=cx;(4)y=dx.
则a,b,c,d与1的大小关系是 ( )
A.a
[解析] 可先分为两类,(3)(4)的底数一定大于1,(1)(2)的底数一定小于1,然后再由(3)(4)比较,c,d的大小,由(1)(2)比较a,b的大小.当指数函数的底数大于1时,图象上升,且当底数越大,图象向上越靠近y轴;当底数大于0小于1时,图象下降,且当底数越小,图象向下越靠近x轴,故选B.
『规律方法』 指数函数图象的变化规律
指数函数的图象随底数变化的规律可归纳为:在第一象限内,图象自下而上对应的底数依次增大.D [解析] 按规律,C1,C2,C3,C4的底数a依次增大,故选D.(2)若函数y=ax+(b-1)(a>0,且a≠1)的图象不经过第二象限,则有 ( )
A.a>1且b<1 B.0<a<1且b≤1
C.0<a<1且b>0 D.a>1且b≤0
[解析] 由函数图象不过第二象限知a>1,且x=0时,a0+(b-1)≤0,∴b≤0,故选D.D 指数函数中忽视对底数的分类讨论致误典例 5转化与化归思想的应用指数型函数的定义域、值域、图象与性质的讨论都可以化归为基本函数y=ax(a>0且a≠1)的相关知识来解决.[思路分析] (1)题中x-4满足什么条件时,函数有意义?y的值不可能取得什么?
(2)题中式子的指数中含有根式,若要有意义,需满足什么条件?典例 4『规律方法』 1.函数单调性在求函数值域中的应用
(1)若函数f(x)在区间[a,b]上是增函数,则f(a)≤f(x)≤f(b),值域为[f(a),f(b)].
(2)若函数f(x)在区间[a,b]上是减函数,则f(a)≥f(x)≥f(b),值域为[f(b),f(a)].
2.函数y=af(x)定义域、值域的求法
(1)定义域.
函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)值域.
①换元,令t=f(x);②求t=f(x)的定义域x∈D;③求t=f(x)的值域t∈M;④利用y=at的单调性求y=at,t∈M的值域.[解析] 根据指数函数的定义:形如y=ax(a>0,且a≠1)的函数叫做指数函数,结合选项从而可知y=52x=25x为指数函数,故选D.D
2.已知1>n>m>0,则指数函数①y=mx,②y=nx的图象为 ( )
[解析] 由于0<m<n<1,所以y=mx与y=nx都是减函数,故排除A、B项,作直线x=1与两个曲线相交,交点在下面的是函数y=mx的图象,故选C.C 3.(2019·安徽合肥众兴中学高一期末测试)函数y=ax-2+1(a>0且a≠1)的图象必经过点 ( )
A.(0,1) B.(1,1)
C.(2,0) D.(2,2)
[解析] 令x-2=0,即x=2,y=a0+1=2,故选D.D
5.函数y=2x(x≥0)的值域是______________.
[解析] ∵y=2x在[0,+∞)上为增函数,
∴x≥0即y≥20,
∴值域为[1,+∞).[1,+∞)
