高中数学新人教A版必修1课件:第二章基本初等函数2.2.1对数与对数运算(第2课时)对数的运算性质(36张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第二章基本初等函数2.2.1对数与对数运算(第2课时)对数的运算性质(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 656.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:18:02 | ||
图片预览









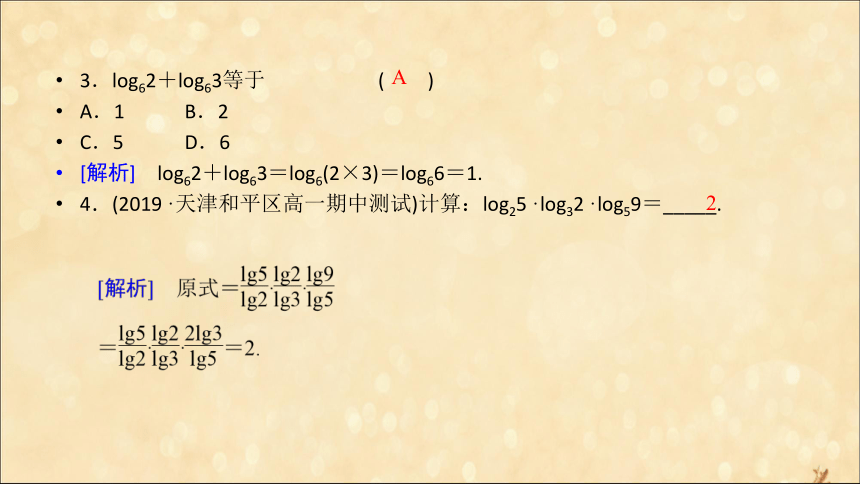


文档简介
课件36张PPT。第二章基本初等函数(Ⅰ)2.2 对数函数2.2.1 对数与对数运算第二课时 对数的运算性质自主预习学案已知对数log864,log264,log28,log464,log48.
对数log864的值与对数log264和log28的值有什么关系?
对数log864的值与对数log464和log48的值有什么关系?
由上面的问题你能得出什么结论?logaM+logaN logaM-logaN nlogaM 2.换底公式
logab=________(a>0,且a≠1;c>0,且c≠1;b>0).A [解析] 由对数运算法则知,均不正确.故选A.B 3.log62+log63等于 ( )
A.1 B.2
C.5 D.6
[解析] log62+log63=log6(2×3)=log66=1.
4.(2019·天津和平区高一期中测试)计算:log25·log32·log59=_____.A 2 互动探究学案命题方向1 ?对数的运算性质典例 1 『规律方法』 对对数式进行计算、化简时,一要注意准确应用对数的性质和运算性质.二要注意取值范围对符号的限制.命题方向2 ?运用对数的运算性质化简求值[思路分析] 利用对数的运算性质进行计算.典例 2『规律方法』 灵活运用对数运算法则进行对数运算,要注意法则的正用和逆用.在化简变形的过程中,要善于观察、比较和分析,从而选择快捷、有效的运算方案进行对数运算.命题方向3 ?换底公式的应用典例 3[思路分析] (1)对数的底数不同,如何将其化为同底的对数?
(2)等式左边前一个对数的真数是后面对数的底数,利用换底公式很容易进行约分求解m的值.
因忽视对数的真数大于零而致误 解方程lg(x+1)+lgx=lg6.
[错解] ∵lg(x+1)+lgx=lg[x(x+1)]=lg(x2+x),
∴lg(x2+x)=lg6,
∴x2+x=6,解得x=2或x=-3.典例 4[正解] ∵lg(x+1)+lgx=lg[x(x+1)]=lg6,
∴x(x+1)=6,解得x=2或x=-3,经检验x=-3不符合题意,∴x=2.转化与化归思想的应用与综合分析解决问题的能力典例 6『规律方法』 1.应用换底公式应注意的事项
(1)注意换底公式的正用、逆用以及变形应用.
(2)题目中有指数式和对数式时,要注意将指数式与对数式统一成一种形式,注意转化与化归思想的运用.
2.对数式的条件求值问题要注意观察所给数字特征,分析找到实现转化的共同点进行转化.
3.利用换底公式计算、化简、求值的一般思路:
思路一:用对数的运算法则及性质进行部分运算→换成同一底数.
思路二:一次性统一换为常用对数(或自然对数)→化简、通分、求值.B
2.2log510+log50.25的值为 ( )
A.0 B.1
C.2 D.4
[解析] 原式=log5100+log50.25
=log5(100×0.25)=log525=log552=2.C
对数log864的值与对数log264和log28的值有什么关系?
对数log864的值与对数log464和log48的值有什么关系?
由上面的问题你能得出什么结论?logaM+logaN logaM-logaN nlogaM 2.换底公式
logab=________(a>0,且a≠1;c>0,且c≠1;b>0).A [解析] 由对数运算法则知,均不正确.故选A.B 3.log62+log63等于 ( )
A.1 B.2
C.5 D.6
[解析] log62+log63=log6(2×3)=log66=1.
4.(2019·天津和平区高一期中测试)计算:log25·log32·log59=_____.A 2 互动探究学案命题方向1 ?对数的运算性质典例 1 『规律方法』 对对数式进行计算、化简时,一要注意准确应用对数的性质和运算性质.二要注意取值范围对符号的限制.命题方向2 ?运用对数的运算性质化简求值[思路分析] 利用对数的运算性质进行计算.典例 2『规律方法』 灵活运用对数运算法则进行对数运算,要注意法则的正用和逆用.在化简变形的过程中,要善于观察、比较和分析,从而选择快捷、有效的运算方案进行对数运算.命题方向3 ?换底公式的应用典例 3[思路分析] (1)对数的底数不同,如何将其化为同底的对数?
(2)等式左边前一个对数的真数是后面对数的底数,利用换底公式很容易进行约分求解m的值.
因忽视对数的真数大于零而致误 解方程lg(x+1)+lgx=lg6.
[错解] ∵lg(x+1)+lgx=lg[x(x+1)]=lg(x2+x),
∴lg(x2+x)=lg6,
∴x2+x=6,解得x=2或x=-3.典例 4[正解] ∵lg(x+1)+lgx=lg[x(x+1)]=lg6,
∴x(x+1)=6,解得x=2或x=-3,经检验x=-3不符合题意,∴x=2.转化与化归思想的应用与综合分析解决问题的能力典例 6『规律方法』 1.应用换底公式应注意的事项
(1)注意换底公式的正用、逆用以及变形应用.
(2)题目中有指数式和对数式时,要注意将指数式与对数式统一成一种形式,注意转化与化归思想的运用.
2.对数式的条件求值问题要注意观察所给数字特征,分析找到实现转化的共同点进行转化.
3.利用换底公式计算、化简、求值的一般思路:
思路一:用对数的运算法则及性质进行部分运算→换成同一底数.
思路二:一次性统一换为常用对数(或自然对数)→化简、通分、求值.B
2.2log510+log50.25的值为 ( )
A.0 B.1
C.2 D.4
[解析] 原式=log5100+log50.25
=log5(100×0.25)=log525=log552=2.C
