高中数学新人教A版必修1课件:第二章基本初等函数2.2.2对数函数及其性质(第1课时)对数函数及其性质(32张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第二章基本初等函数2.2.2对数函数及其性质(第1课时)对数函数及其性质(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 841.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:18:47 | ||
图片预览










文档简介
课件32张PPT。第二章基本初等函数(Ⅰ)2.2 对数函数2.2.2 对数函数及其性质第一课时 对数函数及其性质自主预习学案我们所处的地球正当壮年,地壳运动还非常频繁,每年用地震仪可以测出的地震大约有500万次,平均每隔几秒钟就有一次,其中3级以上的大约只有5万次,仅占1%,7级以上的大震每年平均约有18次,8级以上的地震每年平均仅1次,那么地震的震级是怎么定义的呢?这里面就要用到对数函数.1.对数函数的定义
一般地,我们把函数y=____________(a>0,且a≠1)叫做对数函数,其中______是自变量,函数的定义域是_____________.
[知识点拨] (1)由于指数函数y=ax中的底数a满足a>0,且a≠1,则对数函数y=logax中的底数a也必须满足a>0,且a≠1.
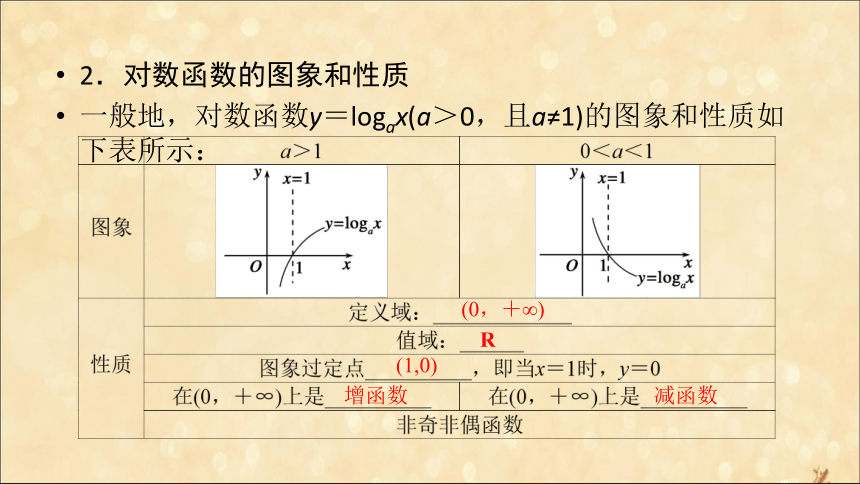
(2)对数函数的解析式同时满足:①对数符号前面的系数是1;②对数的底数是不等于1的正实数(常数);③对数的真数仅有自变量x.logax x (0,+∞) 2.对数函数的图象和性质
一般地,对数函数y=logax(a>0,且a≠1)的图象和性质如下表所示:(0,+∞) R (1,0) 增函数 减函数
3. 反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为反函数,它们的图象关于直线__________对称.y=x 1.下列函数是对数函数的是 ( )
A.y=2+log3x
B.y=loga(2a)(a>0,且a≠1)
C.y=logax2(a>0,且a≠1)
D.y=lnx
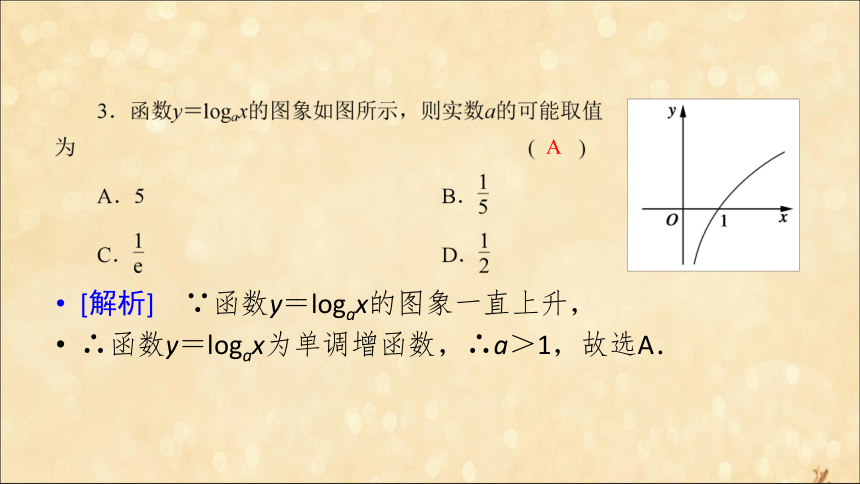
[解析] 判断一个函数是否为对数函数,其关键是看其是否具有“y=logax”的形式,A,B,C全错,D正确.D D A [解析] ∵函数y=logax的图象一直上升,
∴函数y=logax为单调增函数,∴a>1,故选A.
4.(2019·河南永城实验中学高一期末测试)函数y=loga(x-1)(a>0且a≠1)的图象恒过定点__________.
[解析] 令x-1=1,∴x=2,则y=0,故函数y=loga(x-1)(a>0且a≠1)的图象恒过定点(2,0).(2,0) 互动探究学案命题方向1 ?对数函数概念 下列函数表达式中,是对数函数的有 ( )
①y=logx2;②y=logax(a∈R);③y=log8x;④y=lnx;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1).
A.1个 B.2个
C.3个 D.4个
[思路分析] (1)对数概念对底数、真数、系数的要求是什么?B 典例 1
[解析] 根据对数函数的定义进行判断.由于①中自变量出现在底数上,
∴①不是对数函数;由于②中底数a∈R不能保证a>0且a≠1,
∴②不是对数函数;由于⑤、⑦的真数分别为(x+2),(x+1),
∴⑤、⑦也不是对数函数;由于⑥中log4x系数为2,
∴⑥不是对数函数;只有③、④符合对数函数的定义.
『规律方法』 对于对数概念要注意以下两点:
(1)在函数的定义中,a>0且a≠1.
(2)在解析式y=logax中,logax的系数必须为1,真数必须为x,底数a必须是大于0且不等于1的常数.命题方向2 ?对数函数的定义域[思路分析] 依据使函数有意义的条件列出不等式组→解不等式组→写出函数的定义域.典例 2『规律方法』 定义域是研究函数的基础,若已知函数解析式求定义域,常规为:①分母不能为零,②0的零次幂与负指数次幂无意义,③偶次方根的被开方式(数)非负,④求与对数函数有关的函数定义域时,除遵循前面求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意底数;三是按底数的取值应用单调性.C 忽略对数函数的定义域致错 已知函数y=f(x),x,y满足关系式lg(lgy)=lg(3x)+lg(3-x),求函数y=f(x)的解析式、定义域及值域.
[错解] 因为lg(lgy)=lg(3x)+lg(3-x)=lg[3x(3-x)],①
所以lgy=3x(3-x),即y=103x(3-x).
所以定义域为R,值域为(0,+∞).
以上解题过程中都有哪些错误?出错的原因是什么?你如何改正?如何防范?典例 3观察下列对数函数图象,分析底数a的变化对函数图象的影响,你发现了什么规律?
(1)不管a>1还是0(2)在第一象限内,依图象的分布,逆时针方向a逐渐变小,即a的值越小,图象越靠近y轴. 已知图中曲线C1,C2,C3,C4分别是函数y=loga1x,y=log a2x,y=log a3x,y=log a4x的图象,则a1,a2,a3,a4的大小关系是 ( )
A.a4B.a3C.a2D.a32.对数值logax的符号(x>0,a>0且a≠1)规律:“同正异负”.
(1)当01,a>1时,logax>0,即当真数x和底数a同大于(或小于)1时,对数logax>0,即对数值为正数,简称为“同正”;
(2)当01或x>1,03.指数型、对数型函数的图象与性质的讨论,常常要转化为相应指数函数,对数函数的图象与性质的问题.B [解析] 由题意得3=loga8,
∴a3=8,∴a=2.
∴f(x)=log2(x+2),
∴f(2)=log24=2.D
3.y=2x与y=log2x的图象关于 ( )
A.x轴对称 B.直线y=x对称
C.原点对称 D.y轴对称
[解析] 函数y=2x与函数y=log2x是互为反函数,故它们的图象关于直线y=x对称.B -2 [解析] f(-2)=10-2,f[f(-2)]=lg10-2=-2.
5.已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
一般地,我们把函数y=____________(a>0,且a≠1)叫做对数函数,其中______是自变量,函数的定义域是_____________.
[知识点拨] (1)由于指数函数y=ax中的底数a满足a>0,且a≠1,则对数函数y=logax中的底数a也必须满足a>0,且a≠1.
(2)对数函数的解析式同时满足:①对数符号前面的系数是1;②对数的底数是不等于1的正实数(常数);③对数的真数仅有自变量x.logax x (0,+∞) 2.对数函数的图象和性质
一般地,对数函数y=logax(a>0,且a≠1)的图象和性质如下表所示:(0,+∞) R (1,0) 增函数 减函数
3. 反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为反函数,它们的图象关于直线__________对称.y=x 1.下列函数是对数函数的是 ( )
A.y=2+log3x
B.y=loga(2a)(a>0,且a≠1)
C.y=logax2(a>0,且a≠1)
D.y=lnx
[解析] 判断一个函数是否为对数函数,其关键是看其是否具有“y=logax”的形式,A,B,C全错,D正确.D D A [解析] ∵函数y=logax的图象一直上升,
∴函数y=logax为单调增函数,∴a>1,故选A.
4.(2019·河南永城实验中学高一期末测试)函数y=loga(x-1)(a>0且a≠1)的图象恒过定点__________.
[解析] 令x-1=1,∴x=2,则y=0,故函数y=loga(x-1)(a>0且a≠1)的图象恒过定点(2,0).(2,0) 互动探究学案命题方向1 ?对数函数概念 下列函数表达式中,是对数函数的有 ( )
①y=logx2;②y=logax(a∈R);③y=log8x;④y=lnx;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1).
A.1个 B.2个
C.3个 D.4个
[思路分析] (1)对数概念对底数、真数、系数的要求是什么?B 典例 1
[解析] 根据对数函数的定义进行判断.由于①中自变量出现在底数上,
∴①不是对数函数;由于②中底数a∈R不能保证a>0且a≠1,
∴②不是对数函数;由于⑤、⑦的真数分别为(x+2),(x+1),
∴⑤、⑦也不是对数函数;由于⑥中log4x系数为2,
∴⑥不是对数函数;只有③、④符合对数函数的定义.
『规律方法』 对于对数概念要注意以下两点:
(1)在函数的定义中,a>0且a≠1.
(2)在解析式y=logax中,logax的系数必须为1,真数必须为x,底数a必须是大于0且不等于1的常数.命题方向2 ?对数函数的定义域[思路分析] 依据使函数有意义的条件列出不等式组→解不等式组→写出函数的定义域.典例 2『规律方法』 定义域是研究函数的基础,若已知函数解析式求定义域,常规为:①分母不能为零,②0的零次幂与负指数次幂无意义,③偶次方根的被开方式(数)非负,④求与对数函数有关的函数定义域时,除遵循前面求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意底数;三是按底数的取值应用单调性.C 忽略对数函数的定义域致错 已知函数y=f(x),x,y满足关系式lg(lgy)=lg(3x)+lg(3-x),求函数y=f(x)的解析式、定义域及值域.
[错解] 因为lg(lgy)=lg(3x)+lg(3-x)=lg[3x(3-x)],①
所以lgy=3x(3-x),即y=103x(3-x).
所以定义域为R,值域为(0,+∞).
以上解题过程中都有哪些错误?出错的原因是什么?你如何改正?如何防范?典例 3观察下列对数函数图象,分析底数a的变化对函数图象的影响,你发现了什么规律?
(1)不管a>1还是0
A.a4
(1)当0
(2)当0
∴a3=8,∴a=2.
∴f(x)=log2(x+2),
∴f(2)=log24=2.D
3.y=2x与y=log2x的图象关于 ( )
A.x轴对称 B.直线y=x对称
C.原点对称 D.y轴对称
[解析] 函数y=2x与函数y=log2x是互为反函数,故它们的图象关于直线y=x对称.B -2 [解析] f(-2)=10-2,f[f(-2)]=lg10-2=-2.
5.已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
