高中数学新人教A版必修1课件:第三章函数的应用3.1.1方程的根与函数的零点(47张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第三章函数的应用3.1.1方程的根与函数的零点(47张) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览











文档简介
课件47张PPT。第三章函数的应用
一般而言,在理想条件(食物或养料充足,空间条件充裕,气候适宜,没有敌害等)下,种群在一定时期内的增长大致符合“J”型曲线;在有限的环境(空间有限,食物有限,有捕食者存在等)中,种群增长到一定程度(K)后不再增长,曲线呈“S”型.从数学上来看,就需要用不同的函数增长模型来刻画它们.这样,面对不同情况时,如何选择恰当的函数模型描述它们就很重要.下面我们就进行本章的学习——函数的应用.
3.1 函数与方程3.1.1 方程的根与函数的零点自主预习学案
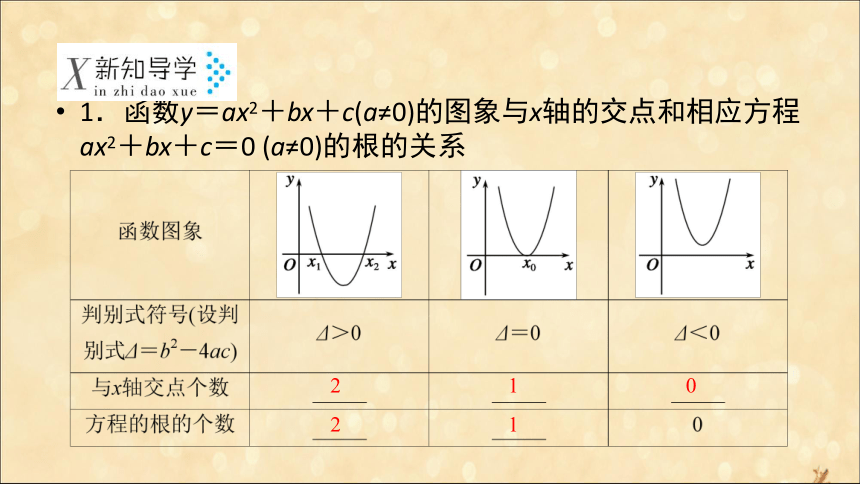
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应方程ax2+bx+c=0 (a≠0)的根的关系2 1 0 2 1
2.函数的零点
(1)定义:对于函数y=f(x),我们把使_____________成立的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与x轴的交点的__________就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有__________?函数y=f(x)的图象与x轴有________?函数y=f(x)有________.
f(x)=0 横坐标 实数根 交点 零点 3.函数零点的判定定理< [知识点拨] 判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.C 2.(2019·广州荔湾区高一期末测试)函数f(x)=x-2+log2x,则f(x)的零点所在区间为 ( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
[解析] f(1)=-1+log21=-1,
f(2)=log22=1,
∴f(1)·f(2)<0,故选B.B
3.若函数f(x)=x2+2x+a没有零点,则实数a的取值范围是 ( )
A.a<1 B.a>1
C.a≤1 D.a≥1
[解析] 函数f(x)=x2+2x+a没有零点,即方程x2+2x+a=0没有实数根,所以Δ=4-4a<0,得a>1.
B
4.二次函数y=ax2+bx+c中,a·c<0,则函数有_____个零点.
[解析] 令ax2+bx+c=0,Δ=b2-4ac,∵a·c<0,
∴b2-4ac>0,∴方程ax2+bx+c=0有两个不相等实根,∴二次函数y=ax2+bx+c(a·c<0)有2个零点.2
[解析] (1)令x2-5x-6=0,得(x-6)(x+1)=0,∴x1=-1,x2=6,∴函数f(x)的零点为-1,6.
(2)令x3-7x+6=0,得x3-x-6x+6=0,
∴x(x+1)(x-1)-6(x-1)=0,
∴(x-1)(x2+x-6)=0,∴(x-1)(x+3)(x-2)=0,
∴x1=-3,x2=1,x3=2.
∴函数f(x)的零点为-3,1,2.互动探究学案命题方向1 ?求函数的零点典例 1 [思路分析] 分别令各个解析式等于0,根据方程是否有根来确定函数的零点.『规律方法』 1.正确理解函数的零点:
(1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.
(2)根据函数零点定义可知,函数f(x)的零点就是f(x)=0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.即函数y=f(x)的零点?方程f(x)=0的实根?函数y=f(x)的图象与x轴交点的横坐标.
2.函数零点的求法:
(1)代数法:求方程f(x)=0的实数根.
(2)几何法:与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.〔跟踪练习1〕
(1)求下列函数的零点:
①f(x)=x2-2x-3零点为__________;
②g(x)=lgx+2零点为______.
(2)已知-1和4是函数f(x)=ax2+bx-4的零点,则f(1)=_______.3,-1 -6 命题方向2 ?判断零点所在的区间 (2019·江西宜丰中学高一期末测试)函数f(x)=lnx+x3-9的零点所在的区间为 ( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
[思路分析] 根据函数零点的存在性原理判断函数零点所在的区间.
[解析] f(1)=1-9=-8<0,f(2)=ln2+8-9=ln2-1<0,
f(3)=ln3+27-9=ln3+18>0,
∴f(2)·f(3)<0,∴函数f(x)的零点所在的区间为(2,3).C 典例 2『规律方法』 判断函数零点所在区间的方法:
一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值,进行符号判断即可得出结论.此类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.〔跟踪练习2〕
函数f(x)=ex+x-2的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)C 命题方向3 ?函数零点个数的判断 函数f(x)=(x-2)(x-5)-1有两个零点x1,x2,且x1A.x1<2,22且x2>5
C.x1<2,x2>5 D.25
[思路分析] f(x)的图象是由g(x)=(x-2)(x-5)的图象向下平移1个单位得到的,由g(x)的零点可判断x1,x2的取值范围.
C 典例 3
[解析] 作出函数g(x)=(x-2)(x-5)的图象如图,将y=g(x)的图象向下平移1个单位即得y=f(x)的图象,由图象易知x1<2,x2>5,故选C.『规律方法』 判断函数零点个数的主要方法:
(1)利用方程根,转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)<0,可判定y=f(x)在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.〔跟踪练习3〕
判断函数f(x)=x-3+lnx的零点的个数.判断零点个数时出现逻辑错误 求函数f(x)=x2-5x+6在[1,4]上的零点个数.
[错解] 错解一:由题意,得f(1)=2>0,f(4)=2>0,因此函数f(x)=x2-5x+6在[1,4]上没有零点,即零点个数是0.
错解二:∵f(1)=2>0,f(2.5)=-0.25<0,∴函数在(1,2.5)内有一个零点;
又∵f(4)=2>0,f(2.5)=-0.25<0,∴函数在(2.5,4)内有一个零点,
∴函数在[1,4]上有两个零点.
[错因分析] 对于错解一,是错误地类比零点存在定理,f(a)·f(b)>0时,(a,b)中的零点情况是不确定的,而错解二出现了逻辑错误,当f(a)·f(b)<0时,(a,b)中存在零点,但个数不确定.典例 5[正解1] 令f(x)=0,即x2-5x+6=0,
∴x1=2,x2=3,
∴函数的零点是2,3.
∴函数在[1,4]上的零点的个数是2.
[正解2] ∵f(1)=2>0,f(2.5)=-0.25<0,f(4)=2>0,
∴f(x)在(1,2.5)和(2.5,4)内都有零点.
又易知f(x)在(-∞,2.5)和(2.5,+∞)上都是单调函数.
∴f(x)在(1,2.5)和(2.5,4)内都只有一个零点.
∴f(x)在[1,4]上有两个零点.
[警示] 当函数y=f(x)的图象在闭区间[a,b]上是一条连续不断的曲线,(1)不满足f(a)·f(b)<0时,函数y=f(x)在区间(a,b)内可能存在零点,也可能不存在零点.(2)满足f(a)·f(b)<0时,f(x)在(a,b)内必有零点,但不一定只有一个零点.1.一元二次方程根的分布问题
(2019·天津市河西区高一期末测试)已知函数f(x)=x2+2mx+3m+4.
(1)若f(x)有且只有一个零点,求实数m的值;
(2)若f(x)有两个零点,且均比-1大,求m的取值范围.
[思路分析] (1)f(x)有且只有一个零点,即方程x2+2mx+3m+4=0有两个相等实数根;
(2)f(x)有两个零点,且均比-1大,即方程x2+2mx+3m+4=0在(-1,+∞)上有两个实数根.典例 5『规律方法』 1.解决一元二次方程根的分布问题,要利用数形结合,结合判别式、对称轴、区间端点的函数值的正负等情况进行求解.
2.二次函数零点的分布问题
二次函数零点的分布一般为下面两个方面的问题:
(1)一个区间内只有一个根;(2)一个区间内有两个根.
由于我们在初中学过方程根的情况,有时可以根据判别式及根与系数的关系判断,但在多数情况下,还要结合图象,从对称轴、判别式、区间端点的函数值等方面去探究.具体解法如下表:
2.数形结合思想
若函数f(x)=|x2-2x|-a没有零点,求实数a的取值范围.
[解析] 由题意令g(x)=|x2-2x|,函数g(x)=|x2-2x|的图象如图.
函数f(x)没有零点,即直线y=a与函数g(x)=|x2-2x|的图象没有交点,观察图象可知,此时a<0.故a的取值范围为(-∞,0).典例 61.下列函数的图象中没有零点的是 ( )
[解析] 从图中观察知,只有D中函数图象与x轴没有交点,故选D.D C 3.(2019·天津和平区高一期中测试)函数f(x)=2x+x的零点所在的一个区间是 ( )
A.(1,2) B.(0,1)
C.(-1,0) D.(-2,-1)C
4.设函数f(x)在区间[a,b]上是单调函数,且f(a)·f(b)<0,则方程f(x)=0在闭区间[a,b]内有_____个根.
[解析] 由f(a)·f(b)<0知f(x)=0在[a,b]上至少有一个实数根,又f(x)在[a,b]上为单调函数,从而可知必有唯一实数根.
1 5.函数f(x)=x2-ax-b的两个零点是2和3,求函数g(x)=bx2-ax-1的零点.
一般而言,在理想条件(食物或养料充足,空间条件充裕,气候适宜,没有敌害等)下,种群在一定时期内的增长大致符合“J”型曲线;在有限的环境(空间有限,食物有限,有捕食者存在等)中,种群增长到一定程度(K)后不再增长,曲线呈“S”型.从数学上来看,就需要用不同的函数增长模型来刻画它们.这样,面对不同情况时,如何选择恰当的函数模型描述它们就很重要.下面我们就进行本章的学习——函数的应用.
3.1 函数与方程3.1.1 方程的根与函数的零点自主预习学案
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应方程ax2+bx+c=0 (a≠0)的根的关系2 1 0 2 1
2.函数的零点
(1)定义:对于函数y=f(x),我们把使_____________成立的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与x轴的交点的__________就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有__________?函数y=f(x)的图象与x轴有________?函数y=f(x)有________.
f(x)=0 横坐标 实数根 交点 零点 3.函数零点的判定定理< [知识点拨] 判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.C 2.(2019·广州荔湾区高一期末测试)函数f(x)=x-2+log2x,则f(x)的零点所在区间为 ( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
[解析] f(1)=-1+log21=-1,
f(2)=log22=1,
∴f(1)·f(2)<0,故选B.B
3.若函数f(x)=x2+2x+a没有零点,则实数a的取值范围是 ( )
A.a<1 B.a>1
C.a≤1 D.a≥1
[解析] 函数f(x)=x2+2x+a没有零点,即方程x2+2x+a=0没有实数根,所以Δ=4-4a<0,得a>1.
B
4.二次函数y=ax2+bx+c中,a·c<0,则函数有_____个零点.
[解析] 令ax2+bx+c=0,Δ=b2-4ac,∵a·c<0,
∴b2-4ac>0,∴方程ax2+bx+c=0有两个不相等实根,∴二次函数y=ax2+bx+c(a·c<0)有2个零点.2
[解析] (1)令x2-5x-6=0,得(x-6)(x+1)=0,∴x1=-1,x2=6,∴函数f(x)的零点为-1,6.
(2)令x3-7x+6=0,得x3-x-6x+6=0,
∴x(x+1)(x-1)-6(x-1)=0,
∴(x-1)(x2+x-6)=0,∴(x-1)(x+3)(x-2)=0,
∴x1=-3,x2=1,x3=2.
∴函数f(x)的零点为-3,1,2.互动探究学案命题方向1 ?求函数的零点典例 1 [思路分析] 分别令各个解析式等于0,根据方程是否有根来确定函数的零点.『规律方法』 1.正确理解函数的零点:
(1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.
(2)根据函数零点定义可知,函数f(x)的零点就是f(x)=0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.即函数y=f(x)的零点?方程f(x)=0的实根?函数y=f(x)的图象与x轴交点的横坐标.
2.函数零点的求法:
(1)代数法:求方程f(x)=0的实数根.
(2)几何法:与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.〔跟踪练习1〕
(1)求下列函数的零点:
①f(x)=x2-2x-3零点为__________;
②g(x)=lgx+2零点为______.
(2)已知-1和4是函数f(x)=ax2+bx-4的零点,则f(1)=_______.3,-1 -6 命题方向2 ?判断零点所在的区间 (2019·江西宜丰中学高一期末测试)函数f(x)=lnx+x3-9的零点所在的区间为 ( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
[思路分析] 根据函数零点的存在性原理判断函数零点所在的区间.
[解析] f(1)=1-9=-8<0,f(2)=ln2+8-9=ln2-1<0,
f(3)=ln3+27-9=ln3+18>0,
∴f(2)·f(3)<0,∴函数f(x)的零点所在的区间为(2,3).C 典例 2『规律方法』 判断函数零点所在区间的方法:
一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值,进行符号判断即可得出结论.此类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.〔跟踪练习2〕
函数f(x)=ex+x-2的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)C 命题方向3 ?函数零点个数的判断 函数f(x)=(x-2)(x-5)-1有两个零点x1,x2,且x1
C.x1<2,x2>5 D.2
[思路分析] f(x)的图象是由g(x)=(x-2)(x-5)的图象向下平移1个单位得到的,由g(x)的零点可判断x1,x2的取值范围.
C 典例 3
[解析] 作出函数g(x)=(x-2)(x-5)的图象如图,将y=g(x)的图象向下平移1个单位即得y=f(x)的图象,由图象易知x1<2,x2>5,故选C.『规律方法』 判断函数零点个数的主要方法:
(1)利用方程根,转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)<0,可判定y=f(x)在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.〔跟踪练习3〕
判断函数f(x)=x-3+lnx的零点的个数.判断零点个数时出现逻辑错误 求函数f(x)=x2-5x+6在[1,4]上的零点个数.
[错解] 错解一:由题意,得f(1)=2>0,f(4)=2>0,因此函数f(x)=x2-5x+6在[1,4]上没有零点,即零点个数是0.
错解二:∵f(1)=2>0,f(2.5)=-0.25<0,∴函数在(1,2.5)内有一个零点;
又∵f(4)=2>0,f(2.5)=-0.25<0,∴函数在(2.5,4)内有一个零点,
∴函数在[1,4]上有两个零点.
[错因分析] 对于错解一,是错误地类比零点存在定理,f(a)·f(b)>0时,(a,b)中的零点情况是不确定的,而错解二出现了逻辑错误,当f(a)·f(b)<0时,(a,b)中存在零点,但个数不确定.典例 5[正解1] 令f(x)=0,即x2-5x+6=0,
∴x1=2,x2=3,
∴函数的零点是2,3.
∴函数在[1,4]上的零点的个数是2.
[正解2] ∵f(1)=2>0,f(2.5)=-0.25<0,f(4)=2>0,
∴f(x)在(1,2.5)和(2.5,4)内都有零点.
又易知f(x)在(-∞,2.5)和(2.5,+∞)上都是单调函数.
∴f(x)在(1,2.5)和(2.5,4)内都只有一个零点.
∴f(x)在[1,4]上有两个零点.
[警示] 当函数y=f(x)的图象在闭区间[a,b]上是一条连续不断的曲线,(1)不满足f(a)·f(b)<0时,函数y=f(x)在区间(a,b)内可能存在零点,也可能不存在零点.(2)满足f(a)·f(b)<0时,f(x)在(a,b)内必有零点,但不一定只有一个零点.1.一元二次方程根的分布问题
(2019·天津市河西区高一期末测试)已知函数f(x)=x2+2mx+3m+4.
(1)若f(x)有且只有一个零点,求实数m的值;
(2)若f(x)有两个零点,且均比-1大,求m的取值范围.
[思路分析] (1)f(x)有且只有一个零点,即方程x2+2mx+3m+4=0有两个相等实数根;
(2)f(x)有两个零点,且均比-1大,即方程x2+2mx+3m+4=0在(-1,+∞)上有两个实数根.典例 5『规律方法』 1.解决一元二次方程根的分布问题,要利用数形结合,结合判别式、对称轴、区间端点的函数值的正负等情况进行求解.
2.二次函数零点的分布问题
二次函数零点的分布一般为下面两个方面的问题:
(1)一个区间内只有一个根;(2)一个区间内有两个根.
由于我们在初中学过方程根的情况,有时可以根据判别式及根与系数的关系判断,但在多数情况下,还要结合图象,从对称轴、判别式、区间端点的函数值等方面去探究.具体解法如下表:
2.数形结合思想
若函数f(x)=|x2-2x|-a没有零点,求实数a的取值范围.
[解析] 由题意令g(x)=|x2-2x|,函数g(x)=|x2-2x|的图象如图.
函数f(x)没有零点,即直线y=a与函数g(x)=|x2-2x|的图象没有交点,观察图象可知,此时a<0.故a的取值范围为(-∞,0).典例 61.下列函数的图象中没有零点的是 ( )
[解析] 从图中观察知,只有D中函数图象与x轴没有交点,故选D.D C 3.(2019·天津和平区高一期中测试)函数f(x)=2x+x的零点所在的一个区间是 ( )
A.(1,2) B.(0,1)
C.(-1,0) D.(-2,-1)C
4.设函数f(x)在区间[a,b]上是单调函数,且f(a)·f(b)<0,则方程f(x)=0在闭区间[a,b]内有_____个根.
[解析] 由f(a)·f(b)<0知f(x)=0在[a,b]上至少有一个实数根,又f(x)在[a,b]上为单调函数,从而可知必有唯一实数根.
1 5.函数f(x)=x2-ax-b的两个零点是2和3,求函数g(x)=bx2-ax-1的零点.
