高中数学新人教A版必修1课件:第三章函数的应用3.1.2用二分法求方程的近似解(34张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第三章函数的应用3.1.2用二分法求方程的近似解(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 558.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:23:37 | ||
图片预览










文档简介
课件34张PPT。第三章函数的应用3.1 函数与方程3.1.2 用二分法求方程的近似解自主预习学案在一档娱乐节目中,主持人让选手在规定时间内猜某物品的价格,若猜中了,就把物品奖给选手.某次竞猜的物品为价格在800元~1 200元之间的一款手机,选手开始报价:
选手:1 000.
主持人:低了.
选手:1 100.主持人:高了.
选手:1 050.
主持人:祝贺你,答对了.
问题1:主持人说“低了”隐含着手机价格在哪个范围内?
问题2:选手每次的报价值同竞猜前手机价格所在范围有何关系?1.二分法的概念
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间____________,使区间的两个端点逐步逼近________,进而得到零点__________的方法叫做二分法.
2.用二分法求函数f(x)的零点近似值的步骤
(1)确定区间[a,b],验证_____________________,给定精确度ε;
(2)求区间(a,b)的中点c;一分为二 零点 近似值 f(a)·f(b)<0
(3)计算f(c):
若f(c)=_____,则c就是函数的零点;
若f(a)·f(c)______0,则令b=c[此时零点x0∈(a,c)];
若f(c)·f(b)______0,则令a=c[此时零点x0∈(c,b)].
(4)判断是否达到精确度ε:
即若|a-b|______ε,则得到零点的近似值为a(或b);否则重复(2)~(4).
3.二分法的应用
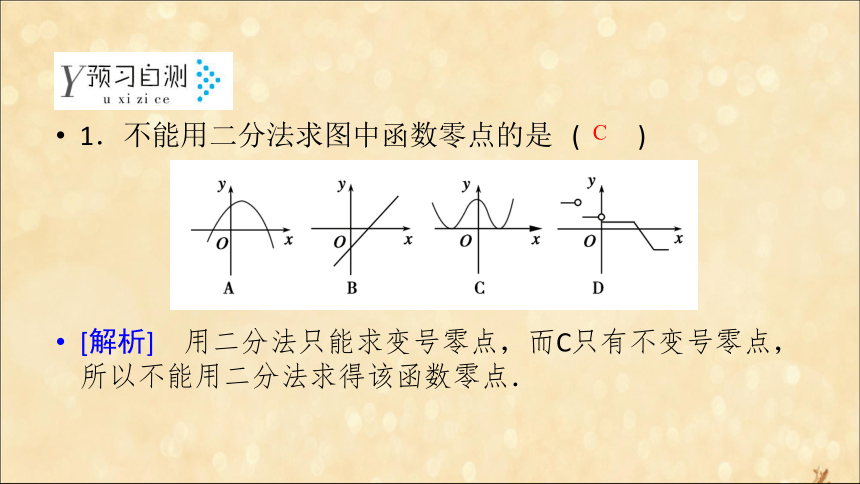
由函数的零点与相应方程根的关系,可以用二分法来求方程的__________.0 < < < 近似解 1.不能用二分法求图中函数零点的是 ( )
[解析] 用二分法只能求变号零点,而C只有不变号零点,所以不能用二分法求得该函数零点.C 2.(2019·河南永城实验中学高一期末测试)用二分法求函数f(x)=x3+5的零点可以取的初始区间是 ( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
[解析] f(-2)=(-2)3+5=-8+5=-3<0,
f(1)=1+5=6>0,
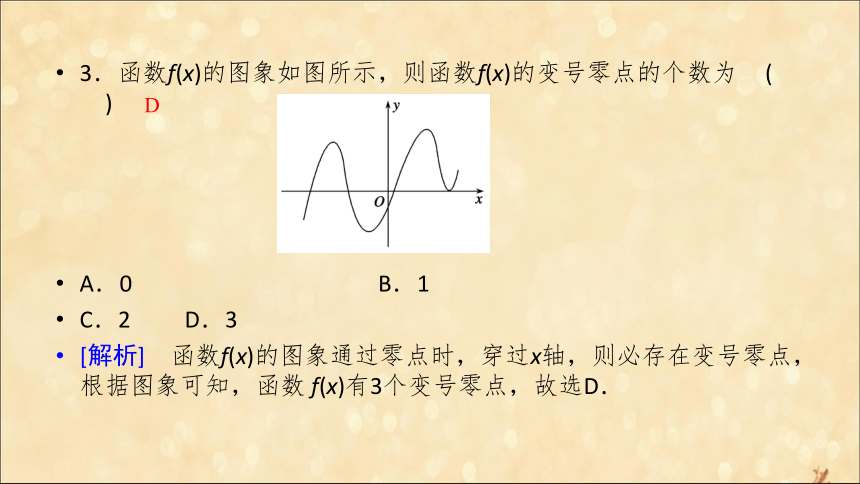
∴f(-2)·f(1)<0,故选A.A 3.函数f(x)的图象如图所示,则函数f(x)的变号零点的个数为 ( )
A.0 B.1
C.2 D.3
[解析] 函数f(x)的图象通过零点时,穿过x轴,则必存在变号零点,根据图象可知,函数 f(x)有3个变号零点,故选D.D
4.方程3x+m=0的根在(-1,0)内,则m的取值范围为__________.(0,3) 5.某电视台有一档娱乐节目,主持人给选手在限定时间内猜某一物品的售价的机会,如果猜中,就把物品奖给选手,同时获得一枚商标.某次节目中要猜一种品牌的手机,手机价格在500~1 000元之间,选手开始报价:1 000元,主持人说高了;700元,低了;880元,高了;850元,低了,851元,恭喜你,猜中了.表面上看猜价格具有很大的碰运气的成分,实际上游戏报价过程体现了“逼近”的数学思想,你能设计出可行的猜价方案来帮助选手猜价吗?
[解析] 取价格区间[500,1 000]的中点750,如果主持人说低了,就再取[750,1 000]的中点875;否则取另一个区间[500,750]的中点.若遇到小数,则取整数,按照这种方案,游戏过程猜价如下:750,875,812,843,859,851,经过6次就可以猜中价格.互动探究学案 (1)下面关于二分法的叙述,正确的是 ( )
A.用二分法可求所有函数零点的近似值
B.用二分法求方程的近似解时,可以精确到小数点后的任一位
C.二分法无规律可循
D.只有在求函数的零点时才用二分法命题方向1 ?对二分法概念的理解B 典例 1
(2)观察下列函数的图象,判断能用二分法求其零点的是 ( )
[思路分析] (1)怎样用二分法求函数的零点?
(2)函数具有零点与该函数的图象有何关系?
A [解析] (1)只有函数的图象在零点附近是连续不断且在该零点左右的函数值异号,才可以用二分法求函数的零点的近似值,故A错;二分法有规律可循,可以通过计算机或计算器来进行,故C错;求方程的近似解也可以用二分法,故D错.
(2)由图象可得,A中零点左侧与右侧的函数值符号不同,故可用二分法求零点.
『规律方法』 运用二分法求函数的零点需具备的两个条件:(1)函数图象在零点附近连续不断;(2)在该零点左右函数值异号.〔跟踪练习1〕
(1)对于二分法求得的近似解,精确度ε说法正确的是 ( )
A.ε越大,零点的精确度越高
B.ε越大,零点的精确度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关B (2)下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的是 ( )
[分析] 解答本题可结合二分法的概念,判断是否具备使用二分法的条件.
[解析] (1)由精确度ε定义知,ε越大,零点的精确度越低.(2)利用二分法求函数零点必须满足零点两侧函数值异号.在B中,不满足f(a)·f(b)<0,不能用二分法求零点,由于A、C、D中零点两侧函数值异号,故可采用二分法求零点.B 命题方向2 ?用二分法求函数的零点问题 用二分法求方程x2-5=0的一个近似解(精确度为0.1).
[思路分析] 典例 2[解析] 令f(x)=x2-5,
因为f(2.2)=2.22-5=-0.16<0,f(2.4)=2.42-5=0.76>0,
所以f(2.2)·f(2.4)<0.
说明函数f(x)在区间(2.2,2.4)内有零点x0.
取区间(2.2,2.4)的中点x1=2.3,f(2.3)=0.29>0.
因为f(2.2)·f(2.3)<0,
所以x0∈(2.2,2.3).再取区间(2.2,2.3)的中点x2=2.25,
f(2.25)=0.0625>0,
因为f(2.2)·f(2.25)<0,所以x0∈(2.2,2.25).
由于|2.25-2.2|=0.05<0.1,所以原方程的近似解可取为2.25.『规律方法』 1.用二分法求函数零点的近似值应遵循的原则
(1)需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法完成).
(2)取区间端点的平均数c,计算f(c),确定有解区间是[m,c]还是[c,n],逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.
2.二分法求函数零点步骤的记忆口诀
定区间,找中点;中值计算两边看,
同号丢,异号算,零点落在异号间.
重复做,何时止,精确度来把关口.A 1.562 5 逆用零点存在性判定定理出错
零点存在性判定定理中,对于区间[a,b]上的连续函数f(x),由f(a)f(b)<0?函数f(x)在区间(a,b)内有零点,而函数f(x)在区间(a,b)内有零点≠f(a)f(b)<0.这两者之间不是等价关系,要加以区分. 若函数f(x)在区间[-2 019,2 019]上的图象是一条连续不断的曲线,且函数f(x)在(-2 019,2 019)内仅有一个零点,则f(-2 019)·f(2 019)的符号是 ( )
A.大于0 B.小于0
C.等于0 D.不能确定
[错解] 由函数零点存在定理得f(-2 019)·f(2 019)<0,故选B.
[错因分析] 根据题目条件,当f(-2 019)·f(2 019)<0时,函数f(x)在区间(-2 019,2 019)内有一个零点,而当函数f(x)在区间(-2 019,2 019)内仅有一个零点时,零点可能是不变号零点(如函数f(x)对应的一元二次方程有二重根),因此f(-2 019)·f(2 019)的符号可能为正号.
[正解] f(-2 019)·f(2 019)的符号不能确定,故选D.D 典例 3
[点评] 注意零点存在定理中,“f(a)f(b)<0”?“函数f(x)在区间(a,b)内有零点”,反向逆推则不成立.如函数f(x)=x2在(-1,1)上有零点0,但是f(-1)·f(1)>0.二分法的数学思想方法是将方程的根看作函数的零点,利用连续函数的性质,将求方程根的问题转化为计算函数值,逐步逼近零点,体现了函数与方程的思想,转化思想,数形结合思想及数学推理.[解析] (1)∵函数y=lnx,y=2x-6在(0,+∞)上都是增函数,
∴f(x)=lnx+2x-6在(0,+∞)上是增函数,
∴f(x)至多有一个零点,由f(2)=ln2-2<0,f(3)=ln3>0,
∴f(2)·f(3)<0,∴f(x)在(2,3)内至少有一个零点,
∴f(x)有且仅有一个零点.典例 4
1.二分法求函数的零点的近似值适合于 ( )
A.零点两侧函数值符号相反 B.零点两侧函数值符号相同
C.都适合 D.都不适合
[解析] 利用二分法求函数的零点,必须满足函数图象连续不断且在零点两侧函数值符号相反.A
2.下列函数不能用二分法求零点的是 ( )
A.f(x)=3x-2 B.f(x)=log2x+2x-9
C.f(x)=(2x-3)2 D.f(x)=3x-3
[解析] 因为f(x)=(2x-3)2≥0,即含有零点的区间[a,b]不满足f(a)·f(b)<0.C 3.函数f(x)的图象是连续不断的曲线,在用二分法求方程f(x)=0在(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的解所在的区间为( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
[解析] 由于f(1.25)f(1.5)<0,则方程的解所在的区间为(1.25,1.5).A (2,3) [解析] ∵f(2)·f(4)<0,f(2)·f(3)<0,
∴f(3)·f(4)>0,∴x0∈(2,3).
选手:1 000.
主持人:低了.
选手:1 100.主持人:高了.
选手:1 050.
主持人:祝贺你,答对了.
问题1:主持人说“低了”隐含着手机价格在哪个范围内?
问题2:选手每次的报价值同竞猜前手机价格所在范围有何关系?1.二分法的概念
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间____________,使区间的两个端点逐步逼近________,进而得到零点__________的方法叫做二分法.
2.用二分法求函数f(x)的零点近似值的步骤
(1)确定区间[a,b],验证_____________________,给定精确度ε;
(2)求区间(a,b)的中点c;一分为二 零点 近似值 f(a)·f(b)<0
(3)计算f(c):
若f(c)=_____,则c就是函数的零点;
若f(a)·f(c)______0,则令b=c[此时零点x0∈(a,c)];
若f(c)·f(b)______0,则令a=c[此时零点x0∈(c,b)].
(4)判断是否达到精确度ε:
即若|a-b|______ε,则得到零点的近似值为a(或b);否则重复(2)~(4).
3.二分法的应用
由函数的零点与相应方程根的关系,可以用二分法来求方程的__________.0 < < < 近似解 1.不能用二分法求图中函数零点的是 ( )
[解析] 用二分法只能求变号零点,而C只有不变号零点,所以不能用二分法求得该函数零点.C 2.(2019·河南永城实验中学高一期末测试)用二分法求函数f(x)=x3+5的零点可以取的初始区间是 ( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
[解析] f(-2)=(-2)3+5=-8+5=-3<0,
f(1)=1+5=6>0,
∴f(-2)·f(1)<0,故选A.A 3.函数f(x)的图象如图所示,则函数f(x)的变号零点的个数为 ( )
A.0 B.1
C.2 D.3
[解析] 函数f(x)的图象通过零点时,穿过x轴,则必存在变号零点,根据图象可知,函数 f(x)有3个变号零点,故选D.D
4.方程3x+m=0的根在(-1,0)内,则m的取值范围为__________.(0,3) 5.某电视台有一档娱乐节目,主持人给选手在限定时间内猜某一物品的售价的机会,如果猜中,就把物品奖给选手,同时获得一枚商标.某次节目中要猜一种品牌的手机,手机价格在500~1 000元之间,选手开始报价:1 000元,主持人说高了;700元,低了;880元,高了;850元,低了,851元,恭喜你,猜中了.表面上看猜价格具有很大的碰运气的成分,实际上游戏报价过程体现了“逼近”的数学思想,你能设计出可行的猜价方案来帮助选手猜价吗?
[解析] 取价格区间[500,1 000]的中点750,如果主持人说低了,就再取[750,1 000]的中点875;否则取另一个区间[500,750]的中点.若遇到小数,则取整数,按照这种方案,游戏过程猜价如下:750,875,812,843,859,851,经过6次就可以猜中价格.互动探究学案 (1)下面关于二分法的叙述,正确的是 ( )
A.用二分法可求所有函数零点的近似值
B.用二分法求方程的近似解时,可以精确到小数点后的任一位
C.二分法无规律可循
D.只有在求函数的零点时才用二分法命题方向1 ?对二分法概念的理解B 典例 1
(2)观察下列函数的图象,判断能用二分法求其零点的是 ( )
[思路分析] (1)怎样用二分法求函数的零点?
(2)函数具有零点与该函数的图象有何关系?
A [解析] (1)只有函数的图象在零点附近是连续不断且在该零点左右的函数值异号,才可以用二分法求函数的零点的近似值,故A错;二分法有规律可循,可以通过计算机或计算器来进行,故C错;求方程的近似解也可以用二分法,故D错.
(2)由图象可得,A中零点左侧与右侧的函数值符号不同,故可用二分法求零点.
『规律方法』 运用二分法求函数的零点需具备的两个条件:(1)函数图象在零点附近连续不断;(2)在该零点左右函数值异号.〔跟踪练习1〕
(1)对于二分法求得的近似解,精确度ε说法正确的是 ( )
A.ε越大,零点的精确度越高
B.ε越大,零点的精确度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关B (2)下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的是 ( )
[分析] 解答本题可结合二分法的概念,判断是否具备使用二分法的条件.
[解析] (1)由精确度ε定义知,ε越大,零点的精确度越低.(2)利用二分法求函数零点必须满足零点两侧函数值异号.在B中,不满足f(a)·f(b)<0,不能用二分法求零点,由于A、C、D中零点两侧函数值异号,故可采用二分法求零点.B 命题方向2 ?用二分法求函数的零点问题 用二分法求方程x2-5=0的一个近似解(精确度为0.1).
[思路分析] 典例 2[解析] 令f(x)=x2-5,
因为f(2.2)=2.22-5=-0.16<0,f(2.4)=2.42-5=0.76>0,
所以f(2.2)·f(2.4)<0.
说明函数f(x)在区间(2.2,2.4)内有零点x0.
取区间(2.2,2.4)的中点x1=2.3,f(2.3)=0.29>0.
因为f(2.2)·f(2.3)<0,
所以x0∈(2.2,2.3).再取区间(2.2,2.3)的中点x2=2.25,
f(2.25)=0.0625>0,
因为f(2.2)·f(2.25)<0,所以x0∈(2.2,2.25).
由于|2.25-2.2|=0.05<0.1,所以原方程的近似解可取为2.25.『规律方法』 1.用二分法求函数零点的近似值应遵循的原则
(1)需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法完成).
(2)取区间端点的平均数c,计算f(c),确定有解区间是[m,c]还是[c,n],逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.
2.二分法求函数零点步骤的记忆口诀
定区间,找中点;中值计算两边看,
同号丢,异号算,零点落在异号间.
重复做,何时止,精确度来把关口.A 1.562 5 逆用零点存在性判定定理出错
零点存在性判定定理中,对于区间[a,b]上的连续函数f(x),由f(a)f(b)<0?函数f(x)在区间(a,b)内有零点,而函数f(x)在区间(a,b)内有零点≠f(a)f(b)<0.这两者之间不是等价关系,要加以区分. 若函数f(x)在区间[-2 019,2 019]上的图象是一条连续不断的曲线,且函数f(x)在(-2 019,2 019)内仅有一个零点,则f(-2 019)·f(2 019)的符号是 ( )
A.大于0 B.小于0
C.等于0 D.不能确定
[错解] 由函数零点存在定理得f(-2 019)·f(2 019)<0,故选B.
[错因分析] 根据题目条件,当f(-2 019)·f(2 019)<0时,函数f(x)在区间(-2 019,2 019)内有一个零点,而当函数f(x)在区间(-2 019,2 019)内仅有一个零点时,零点可能是不变号零点(如函数f(x)对应的一元二次方程有二重根),因此f(-2 019)·f(2 019)的符号可能为正号.
[正解] f(-2 019)·f(2 019)的符号不能确定,故选D.D 典例 3
[点评] 注意零点存在定理中,“f(a)f(b)<0”?“函数f(x)在区间(a,b)内有零点”,反向逆推则不成立.如函数f(x)=x2在(-1,1)上有零点0,但是f(-1)·f(1)>0.二分法的数学思想方法是将方程的根看作函数的零点,利用连续函数的性质,将求方程根的问题转化为计算函数值,逐步逼近零点,体现了函数与方程的思想,转化思想,数形结合思想及数学推理.[解析] (1)∵函数y=lnx,y=2x-6在(0,+∞)上都是增函数,
∴f(x)=lnx+2x-6在(0,+∞)上是增函数,
∴f(x)至多有一个零点,由f(2)=ln2-2<0,f(3)=ln3>0,
∴f(2)·f(3)<0,∴f(x)在(2,3)内至少有一个零点,
∴f(x)有且仅有一个零点.典例 4
1.二分法求函数的零点的近似值适合于 ( )
A.零点两侧函数值符号相反 B.零点两侧函数值符号相同
C.都适合 D.都不适合
[解析] 利用二分法求函数的零点,必须满足函数图象连续不断且在零点两侧函数值符号相反.A
2.下列函数不能用二分法求零点的是 ( )
A.f(x)=3x-2 B.f(x)=log2x+2x-9
C.f(x)=(2x-3)2 D.f(x)=3x-3
[解析] 因为f(x)=(2x-3)2≥0,即含有零点的区间[a,b]不满足f(a)·f(b)<0.C 3.函数f(x)的图象是连续不断的曲线,在用二分法求方程f(x)=0在(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的解所在的区间为( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
[解析] 由于f(1.25)f(1.5)<0,则方程的解所在的区间为(1.25,1.5).A (2,3) [解析] ∵f(2)·f(4)<0,f(2)·f(3)<0,
∴f(3)·f(4)>0,∴x0∈(2,3).
