高中数学新人教A版必修1课件:第三章函数的应用3.2.1几类不同增长的函数模型(32张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第三章函数的应用3.2.1几类不同增长的函数模型(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:24:11 | ||
图片预览











文档简介
课件32张PPT。第三章函数的应用3.2 函数模型及其应用3.2.1 几类不同增长的函数模型自主预习学案
1.四种函数模型的性质增 增 增 增 快 慢 2. 三种增长函数模型的比较
(1)指数函数和幂函数.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长______于xn的增长,因此总存在一个x0,当x>x0时,就会有ax______xn.
(2)对数函数和幂函数.
对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,随着x的增大,logax增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长______于xn的增长,因此总存在一个x0,当x>x0时,就会有logax______xn.快 > 慢 < (3)指数函数、对数函数和幂函数.
在区间(0,+∞)上,尽管函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是______函数,但它们增长的速度不同,而且不在同一个“档次”上,随着x的增大,y=ax(a>1)的增长速度越来越______,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢,因此总存在一个x0,当x>x0时,就会有____________<xn<______.增 快 logax ax
1.当x越来越大时,下列函数中,增长速度最快的是 ( )
A.y=100x B.y=log100x
C.y=x100 D.y=100x
[解析] 由于指数函数的增长是爆炸式增长,则当x越来越大时,函数y=100x的增长速度最快.
D 2.某商品的价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来的价格相比,变化情况是 ( )
A.增加了7.84% B.减少了7.84%
C.减少了9.5% D.不增不减
[解析] 设该商品原价为a,则四年后的价格为a(1+0.2)2(1-0.2)2=a×1.22×0.82=0.921 6a,
所以a-0.921 6a=0.078 4a=7.84%a,
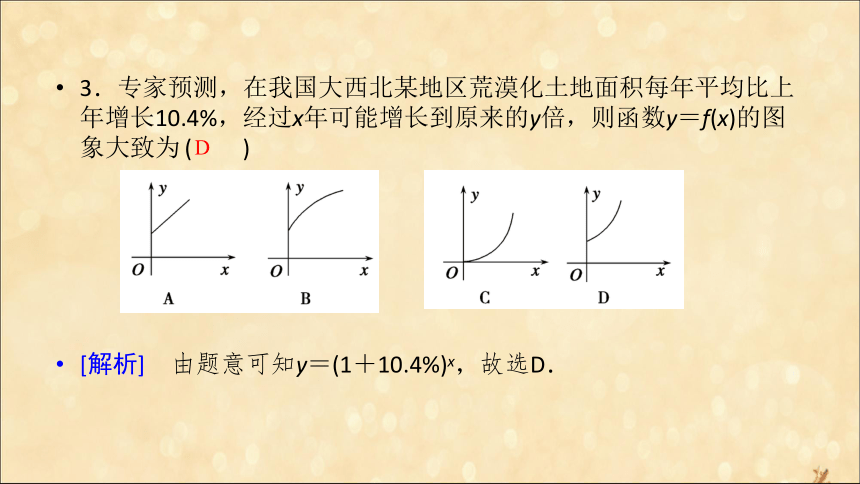
故变化的情况是减少了7.84%.B 3.专家预测,在我国大西北某地区荒漠化土地面积每年平均比上年增长10.4%,经过x年可能增长到原来的y倍,则函数y=f(x)的图象大致为 ( )
[解析] 由题意可知y=(1+10.4%)x,故选D.D 4.某工厂8年来某种产品的总产量C与时间t(年)的函数关系如图,给出下列四种说法:
①前三年中产量增长的速度越来越快;
②前三年中产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是________.
[解析] 由t∈[0,3]的图象,联想到幂函数y=xa(0关于x呈指数函数变化的变量是______.典例 1 y2
[思路分析] (1)从表格观察函数值y1,y2,y3,y4的增加值,哪个变量的增加值最大,则该变量关于x呈指数函数变化.
[解析] 以爆炸式增长的变量呈指数函数变化.
从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速率不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数函数变化.『规律方法』 三种函数模型的增长规律:
(1)对于幂函数y=xn,当x>0,n>0时,y=xn才是增函数,当n越大时,增长速度越快.
(2)指数函数与对数函数的递增前提是a>1,又它们的图象关于y=x对称,从而可知,当a越大,y=ax增长越快;当a越小,y=logax增长越快,一般来说,ax>logax(x>0,a>1).
(3)指数函数与幂函数,当x>0,n>0,a>1时,可能开始时有xn>ax,但因指数函数是爆炸型函数,当x大于某一个确定值x0后,就一定有ax>xn.〔跟踪练习1〕
下面是f(x)随x的增大而得到的函数值表:
试问:(1)随着x的增大,各函数的函数值有什么共同的变化趋势?
(2)各函数增长速度快慢有什么不同?
[解析] (1)随着x的增大,各函数的函数值都在增大.
(2)由图表可以看出:各函数增长速度快慢不同,其中f(x)=2x的增长速度最快,而且越来越快;其次为f(x)=x2,增长的幅度也在变大;而f(x)=2x+7增长速度不变;增长速度最慢的是f(x)=log2x,而且增长的幅度越来越小.命题方向2 ?巧用图象比较大小 已知函数f(x)=2x和g(x)=x3,在同一坐标系下作出了它们的图象,结合图象比较f(8),g(8),f(2 016),g(2 016)的大小.
[思路分析] 已知条件:指数函数解析式f(x)=2x和幂函数解析式g(x)=x3.
条件分析:由函数解析式列表、描点、连线,可得函数图象,由两函数图象的交点,分析函数值的大小情况.典例 2描点、连线,得如图所示图象:
则函数f(x)=2x对应的图象为C2,函数g(x)=x3对应的图象为C1.
∵g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,
f(9)=512,g(10)=1 000,f(10)=1 024,
∴f(1)>g(1),f(2)g(10),
∴1从图象上知,当x1当x>x2时,f(x)>g(x),且g(x)在(0,+∞)上是增函数,
∴f(2 016)>g(2 016)>g(8)>f(8).〔跟踪练习2〕
函数f(x)=lgx,g(x)=0.3x-1的图象如图所示.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
[解析] (1)C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lgx.
(2)当0f(x);当x1g(x);当x>x2时,g(x)>f(x).忽视函数的性质致误 某校为了规范教职工绩效考核制度,现准备拟定一个函数用于根据当月评价分数x(正常情况0≤x≤100,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资y元,要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高的人数要越少,则下列函数最符合要求的是 ( )典例 3C [错解] 由条件知绩效工资不低于500元,且平均分在50分左右,故选A.[错因分析] 错误的根本原因是忽视了绩效分数越高,则绩效工资越高这个条件,实际上本题中的函数应是增函数,且先慢后快,在x=50左右增长缓慢.[警示] 实际应用问题中,要结合问题的实际意义和函数的性质来确定拟合函数.建模思想——函数模型的选择 某皮鞋厂今年1月份开始投产,并且前4个月的产量分别为1万双,1.2万双,1.3万双,1.37万双.由于产品质量好、款式新颖,前几个月的销售情况良好.为了推销员在推销产品时,接受订单不至于过多或过少,需要估计以后几个月的产量.厂里分析,产量的增加是由于工人生产熟练和理顺了生产流程.厂里也暂时不准备增加设备和工人.假如你是厂长,就月份x,产量为y给出三种函数模型:y=ax+b,y=ax2+bx+c,y=abx+c,你将利用哪一种模型去估算以后几个月的产量?
[思路分析] 本题是通过数据验证,确定系数,然后分析确定函数变化情况,最终找出与实际最接近的函数模型.典例 4
结论为:当把x=4代入得y=-0.8×0.54+1.4=1.35.
比较上述三个模拟函数的优劣,既要考虑到误差最小,又要考虑生产的实际,如:增产的趋势和可能性.经过筛选,以指数函数模拟为最佳,一是误差小,二是由于厂房新建,随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过一段时间之后,如果不更新设备,产量必然趋于稳定,而指数函数模型恰好反映了这种趋势.
因此选用指数函数y=-0.8×0.5x+1.4模拟比较接近客观实际.
『规律方法』 本题是对数据进行函数模拟,选择最符合客观实际的模拟函数.一般思路为:先画出散点图,然后作出模拟函数的图象,选择适当的几种函数模型后,再加以验证.函数模型的建立是最大的难点,另外运算量较大,须借助计算器或计算机进行数据处理,函数模型的可靠性与合理性既需要数据检验,又必须符合实际.
1.下列函数中,增长速度最慢的是 ( )
A.y=6x B.y=log6x
C.y=x6 D.y=6x
[解析] 由函数的特征可知,对数函数y=log6x增长速度最慢.B 2.如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为四个选项中的 ( )C 4.某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
1.四种函数模型的性质增 增 增 增 快 慢 2. 三种增长函数模型的比较
(1)指数函数和幂函数.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长______于xn的增长,因此总存在一个x0,当x>x0时,就会有ax______xn.
(2)对数函数和幂函数.
对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,随着x的增大,logax增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长______于xn的增长,因此总存在一个x0,当x>x0时,就会有logax______xn.快 > 慢 < (3)指数函数、对数函数和幂函数.
在区间(0,+∞)上,尽管函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是______函数,但它们增长的速度不同,而且不在同一个“档次”上,随着x的增大,y=ax(a>1)的增长速度越来越______,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢,因此总存在一个x0,当x>x0时,就会有____________<xn<______.增 快 logax ax
1.当x越来越大时,下列函数中,增长速度最快的是 ( )
A.y=100x B.y=log100x
C.y=x100 D.y=100x
[解析] 由于指数函数的增长是爆炸式增长,则当x越来越大时,函数y=100x的增长速度最快.
D 2.某商品的价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来的价格相比,变化情况是 ( )
A.增加了7.84% B.减少了7.84%
C.减少了9.5% D.不增不减
[解析] 设该商品原价为a,则四年后的价格为a(1+0.2)2(1-0.2)2=a×1.22×0.82=0.921 6a,
所以a-0.921 6a=0.078 4a=7.84%a,
故变化的情况是减少了7.84%.B 3.专家预测,在我国大西北某地区荒漠化土地面积每年平均比上年增长10.4%,经过x年可能增长到原来的y倍,则函数y=f(x)的图象大致为 ( )
[解析] 由题意可知y=(1+10.4%)x,故选D.D 4.某工厂8年来某种产品的总产量C与时间t(年)的函数关系如图,给出下列四种说法:
①前三年中产量增长的速度越来越快;
②前三年中产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是________.
[解析] 由t∈[0,3]的图象,联想到幂函数y=xa(0
[思路分析] (1)从表格观察函数值y1,y2,y3,y4的增加值,哪个变量的增加值最大,则该变量关于x呈指数函数变化.
[解析] 以爆炸式增长的变量呈指数函数变化.
从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速率不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数函数变化.『规律方法』 三种函数模型的增长规律:
(1)对于幂函数y=xn,当x>0,n>0时,y=xn才是增函数,当n越大时,增长速度越快.
(2)指数函数与对数函数的递增前提是a>1,又它们的图象关于y=x对称,从而可知,当a越大,y=ax增长越快;当a越小,y=logax增长越快,一般来说,ax>logax(x>0,a>1).
(3)指数函数与幂函数,当x>0,n>0,a>1时,可能开始时有xn>ax,但因指数函数是爆炸型函数,当x大于某一个确定值x0后,就一定有ax>xn.〔跟踪练习1〕
下面是f(x)随x的增大而得到的函数值表:
试问:(1)随着x的增大,各函数的函数值有什么共同的变化趋势?
(2)各函数增长速度快慢有什么不同?
[解析] (1)随着x的增大,各函数的函数值都在增大.
(2)由图表可以看出:各函数增长速度快慢不同,其中f(x)=2x的增长速度最快,而且越来越快;其次为f(x)=x2,增长的幅度也在变大;而f(x)=2x+7增长速度不变;增长速度最慢的是f(x)=log2x,而且增长的幅度越来越小.命题方向2 ?巧用图象比较大小 已知函数f(x)=2x和g(x)=x3,在同一坐标系下作出了它们的图象,结合图象比较f(8),g(8),f(2 016),g(2 016)的大小.
[思路分析] 已知条件:指数函数解析式f(x)=2x和幂函数解析式g(x)=x3.
条件分析:由函数解析式列表、描点、连线,可得函数图象,由两函数图象的交点,分析函数值的大小情况.典例 2描点、连线,得如图所示图象:
则函数f(x)=2x对应的图象为C2,函数g(x)=x3对应的图象为C1.
∵g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,
f(9)=512,g(10)=1 000,f(10)=1 024,
∴f(1)>g(1),f(2)
∴1
∴f(2 016)>g(2 016)>g(8)>f(8).〔跟踪练习2〕
函数f(x)=lgx,g(x)=0.3x-1的图象如图所示.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
[解析] (1)C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lgx.
(2)当0
[思路分析] 本题是通过数据验证,确定系数,然后分析确定函数变化情况,最终找出与实际最接近的函数模型.典例 4
结论为:当把x=4代入得y=-0.8×0.54+1.4=1.35.
比较上述三个模拟函数的优劣,既要考虑到误差最小,又要考虑生产的实际,如:增产的趋势和可能性.经过筛选,以指数函数模拟为最佳,一是误差小,二是由于厂房新建,随着工人技术和管理效益逐渐提高,一段时间内产量会明显上升,但经过一段时间之后,如果不更新设备,产量必然趋于稳定,而指数函数模型恰好反映了这种趋势.
因此选用指数函数y=-0.8×0.5x+1.4模拟比较接近客观实际.
『规律方法』 本题是对数据进行函数模拟,选择最符合客观实际的模拟函数.一般思路为:先画出散点图,然后作出模拟函数的图象,选择适当的几种函数模型后,再加以验证.函数模型的建立是最大的难点,另外运算量较大,须借助计算器或计算机进行数据处理,函数模型的可靠性与合理性既需要数据检验,又必须符合实际.
1.下列函数中,增长速度最慢的是 ( )
A.y=6x B.y=log6x
C.y=x6 D.y=6x
[解析] 由函数的特征可知,对数函数y=log6x增长速度最慢.B 2.如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为四个选项中的 ( )C 4.某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
