高中数学新人教A版必修1课件:第一章集合与函数概念1.1.3集合的基本运算(第1课时)并集和交集(36张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第一章集合与函数概念1.1.3集合的基本运算(第1课时)并集和交集(36张) |  | |
| 格式 | zip | ||
| 文件大小 | 641.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:30:18 | ||
图片预览











文档简介
课件36张PPT。第一章集合与函数概念1.1 集 合1.1.3 集合的基本运算第一课时 并集和交集自主预习学案已知一个班有30人,其中5人有兄弟,5人有姐妹,你能判断这个班有多少是独生子女吗?如果不能判断,你能说出需哪些条件才能对这一问题做出判断吗?
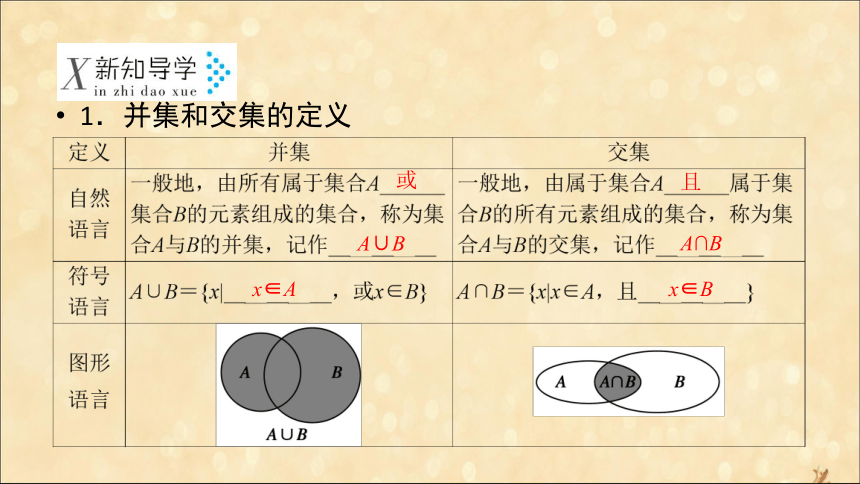
事实上,如果注意到“有兄弟的人也可能有姐妹”,我们就知道,上面给出的条件不足以判断这个班独生子女的人数,为了解决这个问题,我们还必须知道“有兄弟且有姐妹的同学的人数”.应用本小节集合运算的知识,我们就能清晰地描述并解决上述问题了.1.并集和交集的定义或 A∪B 且 A∩B x∈A x∈B
[知识点拨] (1)简单地说,集合A和集合B的全部(公共)元素组成的集合就是集合A与B的并(交)集;(2)当集合A,B无公共元素时,不能说A与B没有交集,只能说它们的交集是空集;(3)在两个集合的并集中,属于集合A且属于集合B的元素只显示一次;(4)交集与并集的相同点是:由两个集合确定一个新的集合,不同点是:生成新集合的法则不同.
2.并集和交集的性质A A A ? 1.(2019·全国卷Ⅲ理,1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B= ( )
A.{-1,0,1} B.{0,1}
C.{-1,1} D.{0,1,2}
[解析] ∵B={x|x2≤1}={x|-1≤x≤1},
∴A∩B={-1,0,1,2}∩{x|-1≤x≤1}={-1,0,1},故选A.
A 2.(2019·江苏宿迁市高一期末测试)设集合M={0,1,2},N={2,4},则M∪N= ( )
A.{0,1,2} B.{2}
C.{2,4} D.{0,1,2,4}
[解析] M∪N={0,1,2}∪{2,4}={0,1,2,4}.
D 3.(2019·全国卷Ⅰ理,1)已知集合M={x|-4A.{x|-4C.{x|-2[解析] N={x|x2-x-6<0}={x|(x-3)(x+2)<0}={x|-2∴M∩N={x|-4={x|-2C 4.(2019·江苏,1)已知集合A={-1,0,1,6},B={x|x>0,x∈R},则A∩B=____________.
[解析] A∩B={-1,0,1,6}∩{x|x>0,x∈R}={1,6}.
5.已知集合A={1,2,3},B={2,m,4},A∩B={2,3},则m=_____.
[解析] 因为A∩B={2,3},所以3∈B.所以m=3.{1,6} 3 互动探究学案命题方向1 ?并集的概念及运算 (1)设集合A={1,2,3},B={2,3,4,5},求A∪B;
(2)设集合A={x|-3[思路分析] 第(1)题由定义直接求解,第(2)题借助数轴求很方便.典例 1 [解析] (1)A∪B={1,2,3}∪{2,3,4,5}={1,2,3,4,5}.
(2)画出数轴如图所示:
∴A∪B={x|-3(1)对于描述法给出的集合,应先看集合的代表元素是什么,弄清是数集,还是点集……,然后将集合化简,再按定义求解.
(2)求两个集合的并集时要注意利用集合元素的互异性这一属性,重复的元素只能算一个.
(3)对于元素个数无限的集合进行并集运算时,可借助数轴,利用数轴分析法求解,但要注意端点的值能否取到.〔跟踪练习1〕
(1)(2019·江西宜丰中学高一检测)已知集合A={x|-2A.{x|-2C.{x|-2(2)(2019·山东潍坊市高一期末测试)满足条件M∪{a}={a,b}的集合M的个数是 ( )
A.4 B.3
C.2 D.1
[解析] (1)A∪B={x|-2(2)∵M∪{a}={a,b},∴M={b}或M={a,b},故选C.A C 命题方向2 ?交集的概念及其运算 (1)设集合M={-1,0,1},N={x|x2=x}则M∩N= ( )
A.{-1,0,1} B.{0,1}
C.{1} D.{0}
(2)若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于 ( )
A.{x|x≤3或x>4} B.{x|-1C.{x|3≤x<4} D.{x|-2≤x<-1}
(3)已知A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则A∩B=________.B 典例 2D {(1,2)} [解析] (1)N={x|x2=x}={0,1},∴M∩N={0,1},故选B.
(2)将集合A、B表示在数轴上,由数轴可得A∩B={x|-2≤x<-1},故选D.『规律方法』 求集合A∩B的方法与步骤
(1)步骤
①首先要搞清集合A、B的代表元素是什么;
②把所求交集的集合用集合符号表示出来,写成“A∩B”的形式;
③把化简后的集合A、B的所有公共元素都写出来即可(若无公共元素则所求交集为?).(2)方法
①若A、B的代表元素是方程的根,则应先解方程,求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
②若A、B是无限数集,可以利用数轴来求解.但要注意,利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心点表示.〔跟踪练习2〕
(1)(2019·天津和平区高一期中测试)设集合A={1,2,3,4},B={y|y=2x-1,x∈A},则A∩B等于 ( )
A.{1,3} B.{2,4}
C.{2,4,5,7} D.{1,2,3,4,5,7}
(2)(2019·广州荔湾区高一期末测试)设集合A={1,2,4},B={x|x2-4x+m=0},若A∩B={1},则集合B= ( )
A.{-3,1} B.{0,1}
C.{1,5} D.{1,3}A D
[解析] (1)∵A={1,2,3,4},B={y|y=2x-1,x∈A},∴B={1,3,5,7},
∴A∩B={1,3},故选A.
(2)∵A∩B={1},
∴1∈B,
∴1是方程x2-4x+m=0的根,
∴1-4+m=0,∴m=3.
∴B={x|x2-4x+3=0}={x|(x-1)(x-3)=0}={1,3}.命题方向3 ?集合交集、并集运算的性质及应用 已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},且A∪B={-2,1,5},A∩B={-2},则p+q+r=________.
[思路分析] -2是不是方程x2-px-2=0的根?怎样确定集合B?
[解析] ∵A∩B={-2},∴-2∈A且-2∈B,
将x=-2代入x2-px-2=0,得p=-1,∴A={1,-2},
∵A∪B={-2,1,5},A∩B={-2},∴B={-2,5},
∴q=-[(-2)+5]=-3,r=(-2)×5=-10,∴p+q+r=-14.-14 典例 3『规律方法』 利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常遇到A∪B=B,A∩B=A等这类问题,解答时常借助于交集、并集的定义及已知集合间的关系去转化为集合间的关系求解,如A∩B=A?A?B,A∪B=B?A?B.
(2)关注点:当集合A?B时,若集合A不确定,运算时要考虑A=?的情况,否则易漏解.〔跟踪练习3〕
已知集合M={x|2x-4=0},N={x|x2-3x+m=0}.
(1)当m=2时,求M∩N,M∪N;
(2)当M∩N=M时,求实数m的值.
[解析] 由已知得M={2},
(1)当m=2时,N={1,2},
所以M∩N={2},M∪N={1,2}.
(2)若M∩N=M,则M?N,
∴2∈N,
所以4-6+m=0,m=2.集合运算时忽略空集致错 集合A={x|x2-3x+2=0},B={x|x2-2x+a-1=0},A∩B=B,求a的取值范围.
[错解] 由题意,得A={1,2}.∵A∩B=B,∴1∈B,或者2∈B,∴a=2或a=1.
[错因分析] A∩B=B?A?B.而B是二次方程的解集,它可能为空集,如果B不为空集,它可能是A的真子集,也可以等于A.
典例 4
[思路分析] A∩B=B,B可能为空集,千万不要忘记.
[正解] 由题意,得A={1,2},∵A∩B=B,当B=?时,(-2)2-4(a-1)<0,解得a>2;
当1∈B时,1-2+a-1=0,解得a=2,且此时B={1},符合题意;
当2∈B时,4-4+a-1=0,解得a=1,此时B={0,2},不合题意;当1∈B且2∈B时,此时a无解.综上所述,a≥2.数形结合思想的应用对于和实数集有关的集合的交集、并集等运算问题,常借助于数轴将集合语言转化为图形语言,或借助Venn图,通过数形结合可直观、形象地看出其解集. 已知集合A={x|0≤x≤4},集合B={x|m+1≤x≤1-m},且A∪B=A,求实数m的取值范围.
[思路分析] 先将A∪B=A等价转化,再借助于数轴直观表达A、B之间的关系,列出关于m的不等式组,解不等式组得到m的取值范围.典例 5『规律方法』 求解此类问题一定要看是否包括端点(临界)值.集合问题大都比较抽象,解题时要尽可能借助Venn图、数轴等工具利用数形结合思想将抽象问题直观化、形象化、明朗化,从而使问题获解.1.(2019·河南永城实验中学高一期末测试)若集合A={x|-1A.{x|1C.{x|-1[解析] A∪B={x|-1={x|-12.设集合A={2,4,6},B={1,3,6},则如图中阴影部分表示的集合是 ( )
A.{2,4,6} B.{1,3,6}
C.{1,2,3,4,6} D.{6}
[解析] 图中阴影表示A∪B,又因为A={2,4,6},B={1,3,6},所以A∪B={1,2,3,4,6},故选C.C 3.(2019·天津文,1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B= ( )
A.{2} B.{2,3}
C.{-1,2,3} D.{1,2,3,4}
[解析] ∵A∩C={-1,1,2,3,5}∩{x∈R|1≤x<3}={1,2},
∴(A∩C)∪B={1,2}∪{2,3,4}={1,2,3,4},故选D.D 4.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是_________.
[解析] 利用数轴画图解题.
要使A∪B=R,则a≤1.a≤1
5.设集合A={a2,-3,9},B={4,-3,8},若A∩B={4,-3},求实数a的值.
[解析] ∵A∩B={4,-3},∴4∈A.
∴a2=4,a=±2.
∴实数a的值为±2.
事实上,如果注意到“有兄弟的人也可能有姐妹”,我们就知道,上面给出的条件不足以判断这个班独生子女的人数,为了解决这个问题,我们还必须知道“有兄弟且有姐妹的同学的人数”.应用本小节集合运算的知识,我们就能清晰地描述并解决上述问题了.1.并集和交集的定义或 A∪B 且 A∩B x∈A x∈B
[知识点拨] (1)简单地说,集合A和集合B的全部(公共)元素组成的集合就是集合A与B的并(交)集;(2)当集合A,B无公共元素时,不能说A与B没有交集,只能说它们的交集是空集;(3)在两个集合的并集中,属于集合A且属于集合B的元素只显示一次;(4)交集与并集的相同点是:由两个集合确定一个新的集合,不同点是:生成新集合的法则不同.
2.并集和交集的性质A A A ? 1.(2019·全国卷Ⅲ理,1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B= ( )
A.{-1,0,1} B.{0,1}
C.{-1,1} D.{0,1,2}
[解析] ∵B={x|x2≤1}={x|-1≤x≤1},
∴A∩B={-1,0,1,2}∩{x|-1≤x≤1}={-1,0,1},故选A.
A 2.(2019·江苏宿迁市高一期末测试)设集合M={0,1,2},N={2,4},则M∪N= ( )
A.{0,1,2} B.{2}
C.{2,4} D.{0,1,2,4}
[解析] M∪N={0,1,2}∪{2,4}={0,1,2,4}.
D 3.(2019·全国卷Ⅰ理,1)已知集合M={x|-4
[解析] A∩B={-1,0,1,6}∩{x|x>0,x∈R}={1,6}.
5.已知集合A={1,2,3},B={2,m,4},A∩B={2,3},则m=_____.
[解析] 因为A∩B={2,3},所以3∈B.所以m=3.{1,6} 3 互动探究学案命题方向1 ?并集的概念及运算 (1)设集合A={1,2,3},B={2,3,4,5},求A∪B;
(2)设集合A={x|-3
(2)画出数轴如图所示:
∴A∪B={x|-3
(2)求两个集合的并集时要注意利用集合元素的互异性这一属性,重复的元素只能算一个.
(3)对于元素个数无限的集合进行并集运算时,可借助数轴,利用数轴分析法求解,但要注意端点的值能否取到.〔跟踪练习1〕
(1)(2019·江西宜丰中学高一检测)已知集合A={x|-2
A.4 B.3
C.2 D.1
[解析] (1)A∪B={x|-2
A.{-1,0,1} B.{0,1}
C.{1} D.{0}
(2)若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于 ( )
A.{x|x≤3或x>4} B.{x|-1
(3)已知A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则A∩B=________.B 典例 2D {(1,2)} [解析] (1)N={x|x2=x}={0,1},∴M∩N={0,1},故选B.
(2)将集合A、B表示在数轴上,由数轴可得A∩B={x|-2≤x<-1},故选D.『规律方法』 求集合A∩B的方法与步骤
(1)步骤
①首先要搞清集合A、B的代表元素是什么;
②把所求交集的集合用集合符号表示出来,写成“A∩B”的形式;
③把化简后的集合A、B的所有公共元素都写出来即可(若无公共元素则所求交集为?).(2)方法
①若A、B的代表元素是方程的根,则应先解方程,求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则A∩B是指两个方程组成的方程组的解集,解集是点集.
②若A、B是无限数集,可以利用数轴来求解.但要注意,利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心点表示.〔跟踪练习2〕
(1)(2019·天津和平区高一期中测试)设集合A={1,2,3,4},B={y|y=2x-1,x∈A},则A∩B等于 ( )
A.{1,3} B.{2,4}
C.{2,4,5,7} D.{1,2,3,4,5,7}
(2)(2019·广州荔湾区高一期末测试)设集合A={1,2,4},B={x|x2-4x+m=0},若A∩B={1},则集合B= ( )
A.{-3,1} B.{0,1}
C.{1,5} D.{1,3}A D
[解析] (1)∵A={1,2,3,4},B={y|y=2x-1,x∈A},∴B={1,3,5,7},
∴A∩B={1,3},故选A.
(2)∵A∩B={1},
∴1∈B,
∴1是方程x2-4x+m=0的根,
∴1-4+m=0,∴m=3.
∴B={x|x2-4x+3=0}={x|(x-1)(x-3)=0}={1,3}.命题方向3 ?集合交集、并集运算的性质及应用 已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},且A∪B={-2,1,5},A∩B={-2},则p+q+r=________.
[思路分析] -2是不是方程x2-px-2=0的根?怎样确定集合B?
[解析] ∵A∩B={-2},∴-2∈A且-2∈B,
将x=-2代入x2-px-2=0,得p=-1,∴A={1,-2},
∵A∪B={-2,1,5},A∩B={-2},∴B={-2,5},
∴q=-[(-2)+5]=-3,r=(-2)×5=-10,∴p+q+r=-14.-14 典例 3『规律方法』 利用集合交集、并集的性质解题的方法及关注点
(1)方法:利用集合的交集、并集性质解题时,常常遇到A∪B=B,A∩B=A等这类问题,解答时常借助于交集、并集的定义及已知集合间的关系去转化为集合间的关系求解,如A∩B=A?A?B,A∪B=B?A?B.
(2)关注点:当集合A?B时,若集合A不确定,运算时要考虑A=?的情况,否则易漏解.〔跟踪练习3〕
已知集合M={x|2x-4=0},N={x|x2-3x+m=0}.
(1)当m=2时,求M∩N,M∪N;
(2)当M∩N=M时,求实数m的值.
[解析] 由已知得M={2},
(1)当m=2时,N={1,2},
所以M∩N={2},M∪N={1,2}.
(2)若M∩N=M,则M?N,
∴2∈N,
所以4-6+m=0,m=2.集合运算时忽略空集致错 集合A={x|x2-3x+2=0},B={x|x2-2x+a-1=0},A∩B=B,求a的取值范围.
[错解] 由题意,得A={1,2}.∵A∩B=B,∴1∈B,或者2∈B,∴a=2或a=1.
[错因分析] A∩B=B?A?B.而B是二次方程的解集,它可能为空集,如果B不为空集,它可能是A的真子集,也可以等于A.
典例 4
[思路分析] A∩B=B,B可能为空集,千万不要忘记.
[正解] 由题意,得A={1,2},∵A∩B=B,当B=?时,(-2)2-4(a-1)<0,解得a>2;
当1∈B时,1-2+a-1=0,解得a=2,且此时B={1},符合题意;
当2∈B时,4-4+a-1=0,解得a=1,此时B={0,2},不合题意;当1∈B且2∈B时,此时a无解.综上所述,a≥2.数形结合思想的应用对于和实数集有关的集合的交集、并集等运算问题,常借助于数轴将集合语言转化为图形语言,或借助Venn图,通过数形结合可直观、形象地看出其解集. 已知集合A={x|0≤x≤4},集合B={x|m+1≤x≤1-m},且A∪B=A,求实数m的取值范围.
[思路分析] 先将A∪B=A等价转化,再借助于数轴直观表达A、B之间的关系,列出关于m的不等式组,解不等式组得到m的取值范围.典例 5『规律方法』 求解此类问题一定要看是否包括端点(临界)值.集合问题大都比较抽象,解题时要尽可能借助Venn图、数轴等工具利用数形结合思想将抽象问题直观化、形象化、明朗化,从而使问题获解.1.(2019·河南永城实验中学高一期末测试)若集合A={x|-1
A.{2,4,6} B.{1,3,6}
C.{1,2,3,4,6} D.{6}
[解析] 图中阴影表示A∪B,又因为A={2,4,6},B={1,3,6},所以A∪B={1,2,3,4,6},故选C.C 3.(2019·天津文,1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B= ( )
A.{2} B.{2,3}
C.{-1,2,3} D.{1,2,3,4}
[解析] ∵A∩C={-1,1,2,3,5}∩{x∈R|1≤x<3}={1,2},
∴(A∩C)∪B={1,2}∪{2,3,4}={1,2,3,4},故选D.D 4.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是_________.
[解析] 利用数轴画图解题.
要使A∪B=R,则a≤1.a≤1
5.设集合A={a2,-3,9},B={4,-3,8},若A∩B={4,-3},求实数a的值.
[解析] ∵A∩B={4,-3},∴4∈A.
∴a2=4,a=±2.
∴实数a的值为±2.
