高中数学新人教A版必修1课件:第一章集合与函数概念1.2.2函数的表示法(第1课时)函数的表示法(35张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第一章集合与函数概念1.2.2函数的表示法(第1课时)函数的表示法(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 792.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览










文档简介
课件35张PPT。第一章集合与函数概念1.2 函数及其表示1.2.2 函数的表示法第一课时 函数的表示法自主预习学案如果一个人极有才华,我们会用“才高八斗”来形容他;如果一个人兼有文武才能,我们会用“出将入相”来形容他;如果一个人是稀有而可贵的人才,我们会用“凤毛麟角”来形容他;如果一个人品行卓越,天下绝无仅有,我们会用“斗南一人”来形容他.那么对于函数,又有哪些不同的表示方法呢?函数的表示法图象 表格 [知识点拨] 三种表示法的优缺点如下表:B [解析] 因为π2∈R,所以f(π2)=π.B [解析] 把考试次数组成的集合看作A={1,2,3,4,5},成绩组成的集合看作B={90,102,105,106},
∴集合A中的任一个数在集合B中有唯一一个数与之对应,
∴成绩y是考试次数x的函数.
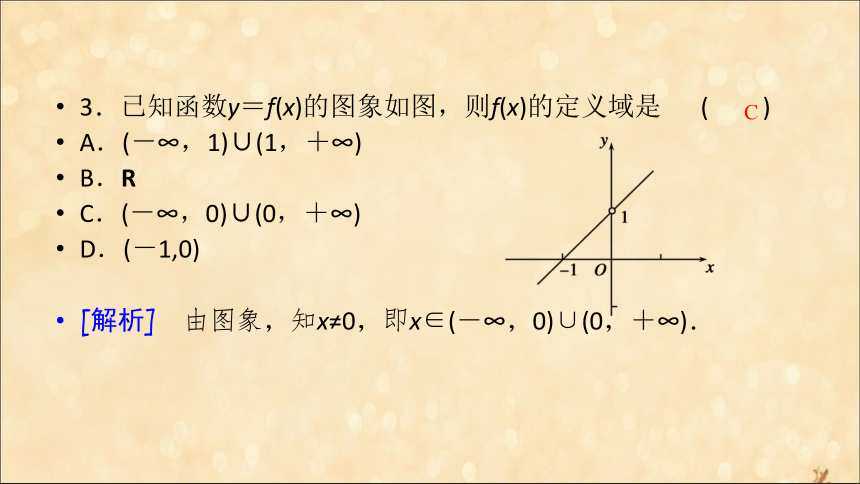
3.已知函数y=f(x)的图象如图,则f(x)的定义域是 ( )
A.(-∞,1)∪(1,+∞)
B.R
C.(-∞,0)∪(0,+∞)
D.(-1,0)
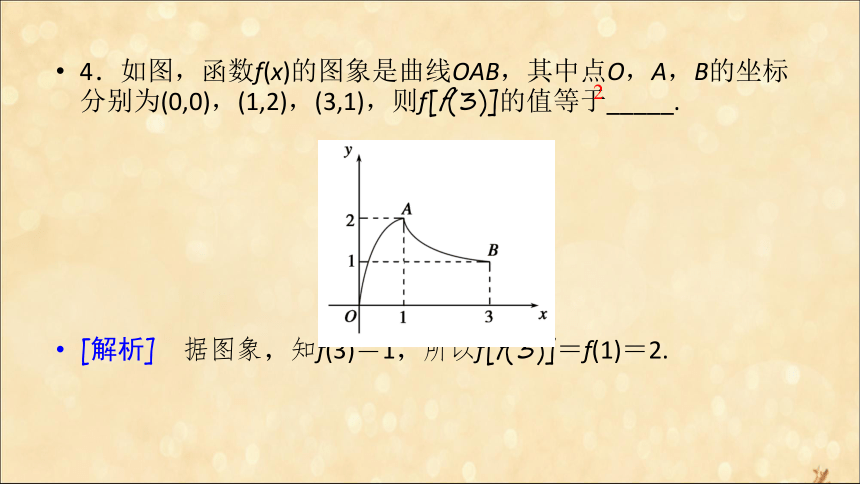
[解析] 由图象,知x≠0,即x∈(-∞,0)∪(0,+∞).C 4.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[f(3)]的值等于_____.
[解析] 据图象,知f(3)=1,所以f[f(3)]=f(1)=2.2 互动探究学案命题方向1 ?函数的三种表示方法 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
[思路分析] 函数的定义域是{1,2,3,…,10},值域是{3 000,6 000,9 000,…,30 000},可直接列表、画图表示.分析题意得到表达y与x关系的解析式,注意定义域.典例 1 『规律方法』 列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在应用三种方法表示函数时要注意:
(1)解析法:必须注明函数的定义域;
(2)列表法:选取的自变量要有代表性,应能反映定义域的特征;
(3)图象法:是否连线.〔跟踪练习1〕
将一条长为10 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形.试用多种方法表示两个正方形的面积之和S与其中一段铁丝长x的函数关系.(x属于正整数集)命题方向2 ?与函数图象有关的问题典例 2[思路分析] (1)画函数的图象时首先要注意的是什么?
(2)所给三个函数的大致图象分别是什么形式的?当x∈[0,2]时,图象是直线的一部分,观察图象可知,其值域为[1,5].(3)列表
画图象,图象是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8].
换元求解析式时忽略自变量的取值范围致误典例 3[警示] 利用换元法求函数解析式时,一定要注意保持换元前后自变量的范围不变.求函数解析式的常用方法1.待定系数法
已知函数类型(如一次、二次、正比例、反比例函数等),可先设出函数解析式,再依据所给条件,确定待定系数. 已知f(x)为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析式.
[思路分析] 已知二次函数f(x)的顶点坐标,可设顶点(配方)式,再利用其他条件确定待定系数.
[解析] 由于函数图象的顶点坐标为(1,3),则设f(x)=a(x-1)2+3(a≠0).
∵函数图象过原点(0,0),∴a+3=0,∴a=-3.
故f(x)=-3(x-1)2+3.
即f(x)=-3x2+6x.典例 4
2.恒成立的应用
一般地,若f(x)与g(x)是同类型的函数(或具有相同的表达式),f(x)=g(x)恒成立,则f(x)与g(x)的对应项系数相等.
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x).典例 5 已知f(x)+2f(-x)=x+1,求f(x)的解析式.
[思路分析] 这是关于x的一个恒等式,由于x∈R,∴对任意x∈R,此等式都成立,当x∈R时,-x∈R,因此上述等式对-x也成立.用-x代替原等式中的x,可构造关于f(x)与f(-x)的方程组求解.典例 61.如图,函数f(x)的图象是折线段,其中点A,B,C的坐标分别是(0,4),(2,0),(6,4),则f[f(2)]= ( )
A.0
B.2
C.4
D.6
[解析] 由图象可得f[f(2)]=f(0)=4.C
2.函数y=x2-2x的定义域为{0,1,2,3},那么其值域为 ( )
A.{-1,0,3} B.{0,1,2,3}
C.{y|-1≤y≤3} D.{y|0≤y≤3}
[解析] 把x=0,1,2,3分别代入y=x2-2x中得y的值共三个为-1,0,3,故值域为{-1,0,3}.A 3.某人开车去某地旅行,先沿直线匀速前行了a km,到达目的地后游玩了一段时间,又原路返回匀速行驶了b km(b[解析] 注意理解两坐标轴s,t的含义,这里s是指距起点的距离,不是路程的累加,结合题意可知C符合.故选C.C 4.一个面积为100 cm2的等腰梯形,上底长为x cm,下底长为上底长的3倍,则它的高y与x的函数关系为_________________.5.已知函数f(x)=ax+b,且f(-1)=-4,f(2)=5,
求:(1)a,b的值;(2)f(0)的值.
∴集合A中的任一个数在集合B中有唯一一个数与之对应,
∴成绩y是考试次数x的函数.
3.已知函数y=f(x)的图象如图,则f(x)的定义域是 ( )
A.(-∞,1)∪(1,+∞)
B.R
C.(-∞,0)∪(0,+∞)
D.(-1,0)
[解析] 由图象,知x≠0,即x∈(-∞,0)∪(0,+∞).C 4.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f[f(3)]的值等于_____.
[解析] 据图象,知f(3)=1,所以f[f(3)]=f(1)=2.2 互动探究学案命题方向1 ?函数的三种表示方法 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
[思路分析] 函数的定义域是{1,2,3,…,10},值域是{3 000,6 000,9 000,…,30 000},可直接列表、画图表示.分析题意得到表达y与x关系的解析式,注意定义域.典例 1 『规律方法』 列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在应用三种方法表示函数时要注意:
(1)解析法:必须注明函数的定义域;
(2)列表法:选取的自变量要有代表性,应能反映定义域的特征;
(3)图象法:是否连线.〔跟踪练习1〕
将一条长为10 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形.试用多种方法表示两个正方形的面积之和S与其中一段铁丝长x的函数关系.(x属于正整数集)命题方向2 ?与函数图象有关的问题典例 2[思路分析] (1)画函数的图象时首先要注意的是什么?
(2)所给三个函数的大致图象分别是什么形式的?当x∈[0,2]时,图象是直线的一部分,观察图象可知,其值域为[1,5].(3)列表
画图象,图象是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8].
换元求解析式时忽略自变量的取值范围致误典例 3[警示] 利用换元法求函数解析式时,一定要注意保持换元前后自变量的范围不变.求函数解析式的常用方法1.待定系数法
已知函数类型(如一次、二次、正比例、反比例函数等),可先设出函数解析式,再依据所给条件,确定待定系数. 已知f(x)为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析式.
[思路分析] 已知二次函数f(x)的顶点坐标,可设顶点(配方)式,再利用其他条件确定待定系数.
[解析] 由于函数图象的顶点坐标为(1,3),则设f(x)=a(x-1)2+3(a≠0).
∵函数图象过原点(0,0),∴a+3=0,∴a=-3.
故f(x)=-3(x-1)2+3.
即f(x)=-3x2+6x.典例 4
2.恒成立的应用
一般地,若f(x)与g(x)是同类型的函数(或具有相同的表达式),f(x)=g(x)恒成立,则f(x)与g(x)的对应项系数相等.
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x).典例 5 已知f(x)+2f(-x)=x+1,求f(x)的解析式.
[思路分析] 这是关于x的一个恒等式,由于x∈R,∴对任意x∈R,此等式都成立,当x∈R时,-x∈R,因此上述等式对-x也成立.用-x代替原等式中的x,可构造关于f(x)与f(-x)的方程组求解.典例 61.如图,函数f(x)的图象是折线段,其中点A,B,C的坐标分别是(0,4),(2,0),(6,4),则f[f(2)]= ( )
A.0
B.2
C.4
D.6
[解析] 由图象可得f[f(2)]=f(0)=4.C
2.函数y=x2-2x的定义域为{0,1,2,3},那么其值域为 ( )
A.{-1,0,3} B.{0,1,2,3}
C.{y|-1≤y≤3} D.{y|0≤y≤3}
[解析] 把x=0,1,2,3分别代入y=x2-2x中得y的值共三个为-1,0,3,故值域为{-1,0,3}.A 3.某人开车去某地旅行,先沿直线匀速前行了a km,到达目的地后游玩了一段时间,又原路返回匀速行驶了b km(b
求:(1)a,b的值;(2)f(0)的值.
