高中数学新人教A版必修1课件:第一章集合与函数概念1.3.1单调性与最大(小)值(第1课时)函数的单调性(39张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第一章集合与函数概念1.3.1单调性与最大(小)值(第1课时)函数的单调性(39张) |  | |
| 格式 | zip | ||
| 文件大小 | 986.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:34:02 | ||
图片预览











文档简介
课件39张PPT。第一章集合与函数概念1.3 函数的基本性质1.3.1 单调性与最大(小)值第一课时 函数的单调性自主预习学案
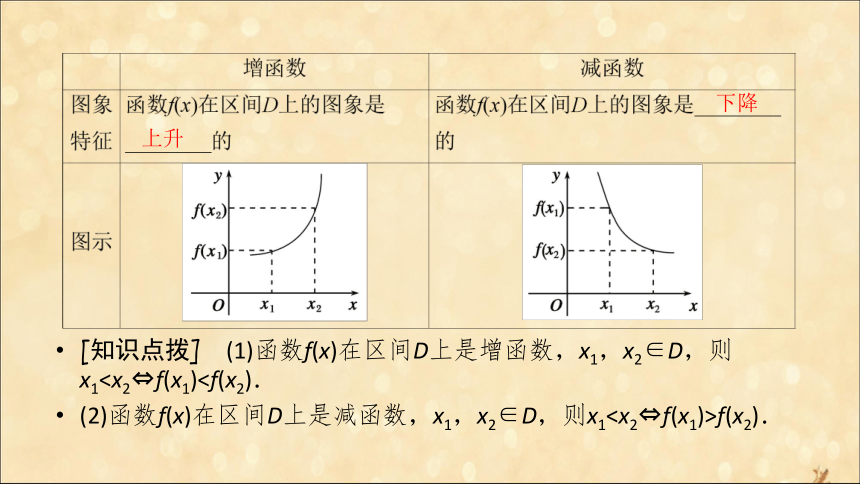
1.增函数和减函数< > 上升 下降 [知识点拨] (1)函数f(x)在区间D上是增函数,x1,x2∈D,则x1(2)函数f(x)在区间D上是减函数,x1,x2∈D,则x1f(x2).
2.单调性
(1)定义:如果函数y=f(x)在区间D上是__________或__________,那么就说函数y=f(x)在区间D上具有(严格的)单调性,区间D叫做函数y=f(x)的____________.
(2)图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.增函数 减函数 单调区间 [归纳总结] 基本初等函数的单调区间如下表所示:1.函数y=f(x)在区间(a,b)上是减函数,x1,x2∈(a,b),且x1<x2,则有 ( )
A.f(x1)C.f(x1)=f(x2) D.以上都有可能
[解析] 因为函数y=f(x)在(a,b)上是减函数,且x1f(x2),故选B.B B [解析] 分别画出各个函数的图象,在区间(0,2)上上升的图象只有B.A 互动探究学案〔跟踪练习1〕
据下列函数图象,指出函数的单调增区间和单调减区间.
[解析] 由图象(1)知此函数的增区间为(-∞,2],[4,+∞),减区间为[2,4].
由图象(2)知,此函数的增区间为(-∞,-1],[1,+∞),减区间为[-1,0),(0,1].命题方向2 ?用定义证明函数的单调性典例 2[思路分析] 利用减函数的定义来证明,其关键是对f(x1)-f(x2)进行变形,尽量化成几个最简单因式的乘积的形式.
2.用定义证明函数单调性时,作差f(x1)-f(x2)后,若f(x)为多项式函数,则“合并同类项”,再因式分解;若f(x)是分式函数,则“先通分”,再因式分解;若f(x)解析式是根式,则先“分子有理化”再分解因式.命题方向3 ?单调性的应用 已知函数f(x)是定义在R上的增函数,且f(3a-7)>f(11+8a),求实数a的取值范围.
[思路分析] 根据函数的单调性定义可知,由两个自变量的大小可以得到相应的函数值的大小,反之,由两个函数值的大小也可以得到相应自变量的大小. 典例 3『规律方法』 利用函数的单调性解函数值的不等式就是利用函数在某个区间内的单调性,去掉对应关系“f”,转化为自变量的不等式,此时一定要注意自变量的限制条件,以防出错.〔跟踪练习3〕
已知函数g(x)是定义在R上为增函数,且g(t)>g(1-2t),求实数t的取值范围.对单调区间和在区间上单调两个概念理解错误 若函数f(x)=x2+2ax+4的单调递减区间是(-∞,2],则实数a的取值范围是_______.
[错解] 函数f(x)的图象的对称轴为直线x=-a,由于函数在区间(-∞,2]上单调递减,因此-a≥2,即a≤-2.
[错因分析] 错解中把单调区间误认为是在区间上单调.
[正解] 因为函数f(x)的单调递减区间为(-∞,2],且函数f(x)的图象的对称轴为直线x=-a,所以有-a=2,即a=-2.-2 典例 4
[警示] 若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子区间上也是单调的,因此f(x)在区间A上单调增(或减)和f(x)的单调增(或减)区间为A不等价.抽象函数单调性的判断与证明所谓抽象函数,一般是指没有给出具体解析式的函数,研究抽象函数的单调性,主要是考查对函数单调性的理解,是一类重要的题型,而证明抽象函数的单调性常采用定义法. 设f(x)是定义在R上的函数,对m,n∈R,恒有f(m+n)=f(m)·f(n)(f(m)≠0,f(n)≠0),且当x>0时,0(1)f(0)=1;
(2)x∈R时,恒有f(x)>0;
(3)f(x)在R上是减函数.
[思路分析] (1)可通过赋值求f(0);(2)可通过f(0)=f[x+(-x)]=f(x)·f(-x)证明f(x)>0;(3)利用定义可证明函数的单调性.典例 5
(3)设x1,x2∈R,且x1则f(x2)=f[x1+(x2-x1)],
∴f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)=f(x1)·f(x2-x1)-f(x1)=f(x1)[f(x2-x1)-1].
由(2)知f(x1)>0,又x2-x1>0,∴0故f(x2)-f(x1)<0,∴f(x)在R上是减函数.
1.函数y=f(x)的图象如图所示,其增区间是 ( )
A.[0,1]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-3,4]
[解析] 结合图象分析可知,函数图象在区间[-3,1]是上升的,故其增区间是[-3,1].C B 3.(2019·山东潍坊市高一期中测试)已知函数f(x)在(-∞,+∞)上是减函数,若a∈R,则 ( )
A.f(a)>f(2a) B.f(a2)C.f(a2+a)[解析] 由图象可知,f(x)的单调递增区间为(-∞,1)和(1,+∞).(-∞,1)和(1,+∞)
1.增函数和减函数< > 上升 下降 [知识点拨] (1)函数f(x)在区间D上是增函数,x1,x2∈D,则x1
2.单调性
(1)定义:如果函数y=f(x)在区间D上是__________或__________,那么就说函数y=f(x)在区间D上具有(严格的)单调性,区间D叫做函数y=f(x)的____________.
(2)图象特征:函数y=f(x)在区间D上具有单调性,则函数y=f(x)在区间D上的图象是上升的或下降的.增函数 减函数 单调区间 [归纳总结] 基本初等函数的单调区间如下表所示:1.函数y=f(x)在区间(a,b)上是减函数,x1,x2∈(a,b),且x1<x2,则有 ( )
A.f(x1)
[解析] 因为函数y=f(x)在(a,b)上是减函数,且x1
据下列函数图象,指出函数的单调增区间和单调减区间.
[解析] 由图象(1)知此函数的增区间为(-∞,2],[4,+∞),减区间为[2,4].
由图象(2)知,此函数的增区间为(-∞,-1],[1,+∞),减区间为[-1,0),(0,1].命题方向2 ?用定义证明函数的单调性典例 2[思路分析] 利用减函数的定义来证明,其关键是对f(x1)-f(x2)进行变形,尽量化成几个最简单因式的乘积的形式.
2.用定义证明函数单调性时,作差f(x1)-f(x2)后,若f(x)为多项式函数,则“合并同类项”,再因式分解;若f(x)是分式函数,则“先通分”,再因式分解;若f(x)解析式是根式,则先“分子有理化”再分解因式.命题方向3 ?单调性的应用 已知函数f(x)是定义在R上的增函数,且f(3a-7)>f(11+8a),求实数a的取值范围.
[思路分析] 根据函数的单调性定义可知,由两个自变量的大小可以得到相应的函数值的大小,反之,由两个函数值的大小也可以得到相应自变量的大小. 典例 3『规律方法』 利用函数的单调性解函数值的不等式就是利用函数在某个区间内的单调性,去掉对应关系“f”,转化为自变量的不等式,此时一定要注意自变量的限制条件,以防出错.〔跟踪练习3〕
已知函数g(x)是定义在R上为增函数,且g(t)>g(1-2t),求实数t的取值范围.对单调区间和在区间上单调两个概念理解错误 若函数f(x)=x2+2ax+4的单调递减区间是(-∞,2],则实数a的取值范围是_______.
[错解] 函数f(x)的图象的对称轴为直线x=-a,由于函数在区间(-∞,2]上单调递减,因此-a≥2,即a≤-2.
[错因分析] 错解中把单调区间误认为是在区间上单调.
[正解] 因为函数f(x)的单调递减区间为(-∞,2],且函数f(x)的图象的对称轴为直线x=-a,所以有-a=2,即a=-2.-2 典例 4
[警示] 若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子区间上也是单调的,因此f(x)在区间A上单调增(或减)和f(x)的单调增(或减)区间为A不等价.抽象函数单调性的判断与证明所谓抽象函数,一般是指没有给出具体解析式的函数,研究抽象函数的单调性,主要是考查对函数单调性的理解,是一类重要的题型,而证明抽象函数的单调性常采用定义法. 设f(x)是定义在R上的函数,对m,n∈R,恒有f(m+n)=f(m)·f(n)(f(m)≠0,f(n)≠0),且当x>0时,0
(2)x∈R时,恒有f(x)>0;
(3)f(x)在R上是减函数.
[思路分析] (1)可通过赋值求f(0);(2)可通过f(0)=f[x+(-x)]=f(x)·f(-x)证明f(x)>0;(3)利用定义可证明函数的单调性.典例 5
(3)设x1,x2∈R,且x1
∴f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)=f(x1)·f(x2-x1)-f(x1)=f(x1)[f(x2-x1)-1].
由(2)知f(x1)>0,又x2-x1>0,∴0
1.函数y=f(x)的图象如图所示,其增区间是 ( )
A.[0,1]
B.[-4,-3]∪[1,4]
C.[-3,1]
D.[-3,4]
[解析] 结合图象分析可知,函数图象在区间[-3,1]是上升的,故其增区间是[-3,1].C B 3.(2019·山东潍坊市高一期中测试)已知函数f(x)在(-∞,+∞)上是减函数,若a∈R,则 ( )
A.f(a)>f(2a) B.f(a2)
