高中数学新人教A版必修1课件:第一章集合与函数概念1.3.2奇偶性(42张)
文档属性
| 名称 | 高中数学新人教A版必修1课件:第一章集合与函数概念1.3.2奇偶性(42张) |  | |
| 格式 | zip | ||
| 文件大小 | 716.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 15:35:08 | ||
图片预览










文档简介
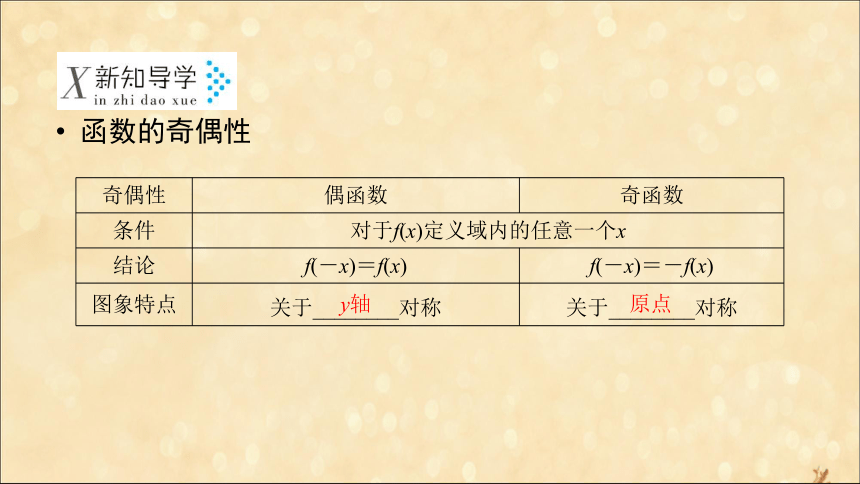
课件42张PPT。第一章集合与函数概念1.3 函数的基本性质1.3.2 奇偶性自主预习学案大自然是一个真正的设计师,它用对称的方法创造了千百万种不同的生命.被誉为“上海之鸟”的浦东国际机场的设计模型,是一只硕大无比、展开双翅的海鸥.它的两翼呈对称状,看上去舒展优美,它象征着浦东将展翅高飞,飞向更高、更广阔的天地,创造更新、更宏伟的业绩.一些函数的图象也有着如此美妙的对称性,那么这种对称性体现了函数的什么性质呢?函数的奇偶性y轴 原点 (3)函数奇偶性的三个关注点.
①若奇函数在原点处有定义,则必有f(0)=0.有时可以用这个结论来否定一个函数为奇函数;
②既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空集合;
③函数根据奇偶性可分为奇函数、偶函数、既奇又偶函数、非奇非偶函数.
(4)奇、偶函数图象对称性的应用.
①若一个函数的图象关于原点对称,则这个函数是奇函数;
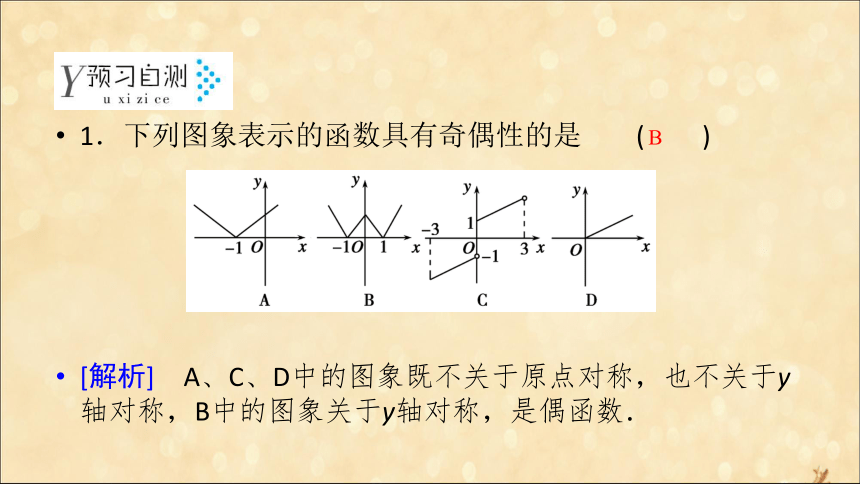
②若一个函数的图象关于y轴对称,则这个函数是偶函数.1.下列图象表示的函数具有奇偶性的是 ( )
[解析] A、C、D中的图象既不关于原点对称,也不关于y轴对称,B中的图象关于y轴对称,是偶函数.B
2.下列函数为偶函数的是 ( )
A.y=x+1 B.y=x2
C.y=x2+x D.y=x3
[解析] y=x+1为非奇非偶函数;y=x2+x为非奇非偶函数;令f(x)=x2,∴f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数;令g(x)=x3,g(-x)=(-x)3=-x3=-g(x),∴g(x)为奇函数.B B -2 互动探究学案命题方向1 ?函数奇偶性的判断典例 1 [思路分析] (1)函数具备奇偶性时,函数的定义域有什么特点?
(2)判断函数的奇偶性应把握好哪几个关键点?『规律方法』 判断函数奇偶性的方法
(1)定义法:
(2)图象法:即若函数的图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.此法多用在解选择题、填空题中.
(3)显然函数f(x)的定义域关于原点对称.
当x>0时,-x<0,f(-x)=x2-x=-(x-x2)=-f(x),
当x<0时,-x>0,f(-x)=-x-x2=-(x2+x)=-f(x),
∴f(-x)=-f(x),∴函数f(x)为奇函数.
(4)由于f(-x)=0=f(x),且f(-x)=0=-f(x),
∴f(x)=0既是奇函数,又是偶函数.
(5)函数f(x)=2x+1的定义域为R,关于原点对称.
∵f(1)=3,f(-1)=-1,-f(1)=-3,
∴f(-1)≠f(1),∴y=2x+1不是偶函数,
又f(-1)≠-f(1),∴y=2x+1不是奇函数,
∴y=2x+1既不是奇函数,又不是偶函数.
(6)函数f(x)的定义域为(-∞,1)∪(1,+∞),不关于原点对称,故函数f(x)不具有奇偶性.命题方向2 ?奇、偶函数图象的应用 已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补全完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间.
[思路分析] ∵函数f(x)为偶函数,∴f(x)的图象关于y轴对称,根据对称性作出函数y=f(x)在x>0时的图象.典例 2[解析] (1)由题意作出函数图象如图:
(2)据图可知,单调增区间为(-1,0),(1,+∞).『规律方法』 1.研究函数图象时,要注意对函数性质的研究,这样可避免作图的盲目性和复杂性.
2.利用函数的奇偶性作图,其依据是奇函数图象关于原点对称,偶函数图象关于y轴对称.命题方向3 ?利用函数的奇偶性求解析式 已知函数y=f(x)的图象关于原点对称,且当x>0时,f(x)=x2-2x+3.试求f(x)在R上的表达式.
[思路分析] (1)如何把(-∞,0)上的未知解析式转移到(0,+∞)上的已知解析式?
(2)奇函数f(x)在x=0处的函数值是多少?由函数图象关于原点对称可知y=f(x)是奇函数.利用奇函数性质可求得解析式.典例 3『规律方法』 利用函数奇偶性求函数解析式
利用函数奇偶性求函数解析式的关键是利用奇偶函数的关系式f(-x)=-f(x)或f(-x)=f(x)成立,但要注意求给定哪个区间的解析式就设这个区间上的变量为x,然后把x转化为-x(另一个已知区间上的解析式中的变量),通过适当推导,求得所求区间上的解析式.〔跟踪练习3〕
已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,求x∈(-∞,0)时,f(x)的解析式 .
[解析] 设x<0,则-x>0,∴f(-x)=(-x)2+(-x)-1=x2-x-1,
∵f(x)为偶函数,∴f(-x)=f(x),∴f(x)=x2-x-1.
∴当x∈(-∞,0)时, f(x)=x2-x-1.忽略函数奇偶性对定义域的限制条件导致判断错误典例 4[错因分析] 要判断函数的奇偶性,必须先求函数定义域(看定义域是否关于原点对称).有时还需要在定义域制约条件下将f(x)进行变形,以利于判定其奇偶性.
[警示] 1.函数y=f(x)是奇函数或偶函数的一个必不可少的条件是定义域关于原点对称.
2.确定函数的定义域时,要针对函数的原解析式.逻辑推理与转化思想的应用——再谈恒成立问题1.在我们数学研究中,存在大量的恒成立问题,如:
(1)f(x)在区间D上单调递增,则对任意x1,x2∈D,当x1(2)若f(x)是奇函数,定义域为M,则f(-x)=-f(x)对任意x∈M恒成立;若f(x)是偶函数,定义域为M,则对任意x∈M, f(-x)=f(x)恒成立;
(3)若f(x)的最大值为M,最小值为m,定义域为A,则对任意x∈A,有m≤f(x)≤M.
解答这类问题时,应充分利用其恒成立的特点选取解答方法.
2.遇到f(-x)与f(x)的关系问题时,应首先从函数f(x)的奇偶性入手考虑,如果f(x)不具有奇偶性,看是否存在奇(偶)函数g(x),使f(x)用g(x)表示,再利用g(x)的奇偶性来解答. 已知f(x)=x5+ax3+bx-8,且f(-2)=10,则f(2)等于 ( )
A.-26 B.-18
C.-10 D.10
[思路分析] 只有一个条件f(-2)=10,两个待定系数a,b,不能通过列方程组方法求出a,b.由f(-2)求f(2),我们可联想函数的奇偶性,观察f(x)的表达式有什么特征?如何借助函数的奇偶性求f(2)?A 典例 5
1.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于 ( )
A.-1 B.0
C.1 D.无法确定
[解析] 由题意得-1+a=0,∴a=1.
C
2.已知函数f(x)=ax2(a>0),则必有 ( )
A.f(a)C.f(a)>f(-a) D.f(a)=f(a+1)
[解析] ∵f(-x)=a(-x)2=ax2=f(x),
∴f(x)为偶函数,∴f(a)=f(-a).
B
3.对于定义域是R的任意奇函数f(x),都有 ( )
A.f(x)-f(-x)>0 B.f(x)-f(-x)≤0
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
[解析] ∵f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),且f(0)=0,
∴f(x)·f(-x)=-f 2(x)≤0,故选C.
4.函数f(x)=x2-2mx+4是偶函数,则实数m=_____.
[解析] f(x)为偶函数,则对称轴为x=m=0.
C 0 5.定义在[-3,-1]∪[1,3]上的函数f(x)是奇函数,其部分图象如图所示.
(1)请在坐标系中补全函数f(x)的图象;
(2)比较f(1)与f(3)的大小.
[解析] (1)因为f(x)是奇函数,所以其图象关于原点对称,如图所示.
(2)观察图象,知f(3)<f(1).
①若奇函数在原点处有定义,则必有f(0)=0.有时可以用这个结论来否定一个函数为奇函数;
②既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空集合;
③函数根据奇偶性可分为奇函数、偶函数、既奇又偶函数、非奇非偶函数.
(4)奇、偶函数图象对称性的应用.
①若一个函数的图象关于原点对称,则这个函数是奇函数;
②若一个函数的图象关于y轴对称,则这个函数是偶函数.1.下列图象表示的函数具有奇偶性的是 ( )
[解析] A、C、D中的图象既不关于原点对称,也不关于y轴对称,B中的图象关于y轴对称,是偶函数.B
2.下列函数为偶函数的是 ( )
A.y=x+1 B.y=x2
C.y=x2+x D.y=x3
[解析] y=x+1为非奇非偶函数;y=x2+x为非奇非偶函数;令f(x)=x2,∴f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数;令g(x)=x3,g(-x)=(-x)3=-x3=-g(x),∴g(x)为奇函数.B B -2 互动探究学案命题方向1 ?函数奇偶性的判断典例 1 [思路分析] (1)函数具备奇偶性时,函数的定义域有什么特点?
(2)判断函数的奇偶性应把握好哪几个关键点?『规律方法』 判断函数奇偶性的方法
(1)定义法:
(2)图象法:即若函数的图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.此法多用在解选择题、填空题中.
(3)显然函数f(x)的定义域关于原点对称.
当x>0时,-x<0,f(-x)=x2-x=-(x-x2)=-f(x),
当x<0时,-x>0,f(-x)=-x-x2=-(x2+x)=-f(x),
∴f(-x)=-f(x),∴函数f(x)为奇函数.
(4)由于f(-x)=0=f(x),且f(-x)=0=-f(x),
∴f(x)=0既是奇函数,又是偶函数.
(5)函数f(x)=2x+1的定义域为R,关于原点对称.
∵f(1)=3,f(-1)=-1,-f(1)=-3,
∴f(-1)≠f(1),∴y=2x+1不是偶函数,
又f(-1)≠-f(1),∴y=2x+1不是奇函数,
∴y=2x+1既不是奇函数,又不是偶函数.
(6)函数f(x)的定义域为(-∞,1)∪(1,+∞),不关于原点对称,故函数f(x)不具有奇偶性.命题方向2 ?奇、偶函数图象的应用 已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补全完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间.
[思路分析] ∵函数f(x)为偶函数,∴f(x)的图象关于y轴对称,根据对称性作出函数y=f(x)在x>0时的图象.典例 2[解析] (1)由题意作出函数图象如图:
(2)据图可知,单调增区间为(-1,0),(1,+∞).『规律方法』 1.研究函数图象时,要注意对函数性质的研究,这样可避免作图的盲目性和复杂性.
2.利用函数的奇偶性作图,其依据是奇函数图象关于原点对称,偶函数图象关于y轴对称.命题方向3 ?利用函数的奇偶性求解析式 已知函数y=f(x)的图象关于原点对称,且当x>0时,f(x)=x2-2x+3.试求f(x)在R上的表达式.
[思路分析] (1)如何把(-∞,0)上的未知解析式转移到(0,+∞)上的已知解析式?
(2)奇函数f(x)在x=0处的函数值是多少?由函数图象关于原点对称可知y=f(x)是奇函数.利用奇函数性质可求得解析式.典例 3『规律方法』 利用函数奇偶性求函数解析式
利用函数奇偶性求函数解析式的关键是利用奇偶函数的关系式f(-x)=-f(x)或f(-x)=f(x)成立,但要注意求给定哪个区间的解析式就设这个区间上的变量为x,然后把x转化为-x(另一个已知区间上的解析式中的变量),通过适当推导,求得所求区间上的解析式.〔跟踪练习3〕
已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,求x∈(-∞,0)时,f(x)的解析式 .
[解析] 设x<0,则-x>0,∴f(-x)=(-x)2+(-x)-1=x2-x-1,
∵f(x)为偶函数,∴f(-x)=f(x),∴f(x)=x2-x-1.
∴当x∈(-∞,0)时, f(x)=x2-x-1.忽略函数奇偶性对定义域的限制条件导致判断错误典例 4[错因分析] 要判断函数的奇偶性,必须先求函数定义域(看定义域是否关于原点对称).有时还需要在定义域制约条件下将f(x)进行变形,以利于判定其奇偶性.
[警示] 1.函数y=f(x)是奇函数或偶函数的一个必不可少的条件是定义域关于原点对称.
2.确定函数的定义域时,要针对函数的原解析式.逻辑推理与转化思想的应用——再谈恒成立问题1.在我们数学研究中,存在大量的恒成立问题,如:
(1)f(x)在区间D上单调递增,则对任意x1,x2∈D,当x1
(3)若f(x)的最大值为M,最小值为m,定义域为A,则对任意x∈A,有m≤f(x)≤M.
解答这类问题时,应充分利用其恒成立的特点选取解答方法.
2.遇到f(-x)与f(x)的关系问题时,应首先从函数f(x)的奇偶性入手考虑,如果f(x)不具有奇偶性,看是否存在奇(偶)函数g(x),使f(x)用g(x)表示,再利用g(x)的奇偶性来解答. 已知f(x)=x5+ax3+bx-8,且f(-2)=10,则f(2)等于 ( )
A.-26 B.-18
C.-10 D.10
[思路分析] 只有一个条件f(-2)=10,两个待定系数a,b,不能通过列方程组方法求出a,b.由f(-2)求f(2),我们可联想函数的奇偶性,观察f(x)的表达式有什么特征?如何借助函数的奇偶性求f(2)?A 典例 5
1.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于 ( )
A.-1 B.0
C.1 D.无法确定
[解析] 由题意得-1+a=0,∴a=1.
C
2.已知函数f(x)=ax2(a>0),则必有 ( )
A.f(a)
[解析] ∵f(-x)=a(-x)2=ax2=f(x),
∴f(x)为偶函数,∴f(a)=f(-a).
B
3.对于定义域是R的任意奇函数f(x),都有 ( )
A.f(x)-f(-x)>0 B.f(x)-f(-x)≤0
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
[解析] ∵f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),且f(0)=0,
∴f(x)·f(-x)=-f 2(x)≤0,故选C.
4.函数f(x)=x2-2mx+4是偶函数,则实数m=_____.
[解析] f(x)为偶函数,则对称轴为x=m=0.
C 0 5.定义在[-3,-1]∪[1,3]上的函数f(x)是奇函数,其部分图象如图所示.
(1)请在坐标系中补全函数f(x)的图象;
(2)比较f(1)与f(3)的大小.
[解析] (1)因为f(x)是奇函数,所以其图象关于原点对称,如图所示.
(2)观察图象,知f(3)<f(1).
