3.2.2 函数模型的应用实例 学案
文档属性
| 名称 | 3.2.2 函数模型的应用实例 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学案 函数模型的应用实例
【知识要点】
1.能利用已知函数模型求解实际问题.
2.能自建确定性函数模型解决实际问题.
3.了解建立拟合函数模型的步骤,并了解检验和调整的必要性.
类型一 利用函数模型求解实际问题
例1某养殖户长期承包一口鱼糖养鱼,每年养殖一批,从鱼苗放入养到成品需要300天,鱼糖承包费用每年5000元,他记录了前几年平均每天投入饲料量(单位:kg)与年底成品鱼(达到一定规格可以销售)产量之间的关系如下表:
平均每天投入饲料(kg) 20 25 30 40 50 60 70 80
成品鱼产量(kg) 2800 3000 3200 3600 3900 4000 3900 3600
(1)请用适当的函数模型描述平均每天投入饲料数量与成品鱼产量之间的关系;
(2)如果今年的饲料价格为1.6元/kg,成品鱼销售价为20元/kg,鱼苗费用4000元,假设养成的成品鱼全部都能按此价格卖出.请建立适当的函数模型分析:平均每天投入饲料多少千克时,该养殖户当年在该鱼糖养殖这种鱼获得的利润最多,最多利润是多少元?(利润=销售收入﹣饲料成本﹣鱼糖承包费﹣鱼苗成本).
跟踪训练1:缴纳个人所得税是收入达到缴纳标准的公民应尽的义务.
①个人所得税率是个人所得税税额与应纳税收入额之间的比例;
②应纳税收入额=月度收入﹣起征点金额﹣专项扣除金额(三险一金等);
③2018年8月31日,第十三届全国人民代表大会常务委员会第五次会议《关于修改中华人民共和国个人所得税法的决定》,将个税免征额(起征点金额)由3500元提高到5000元.
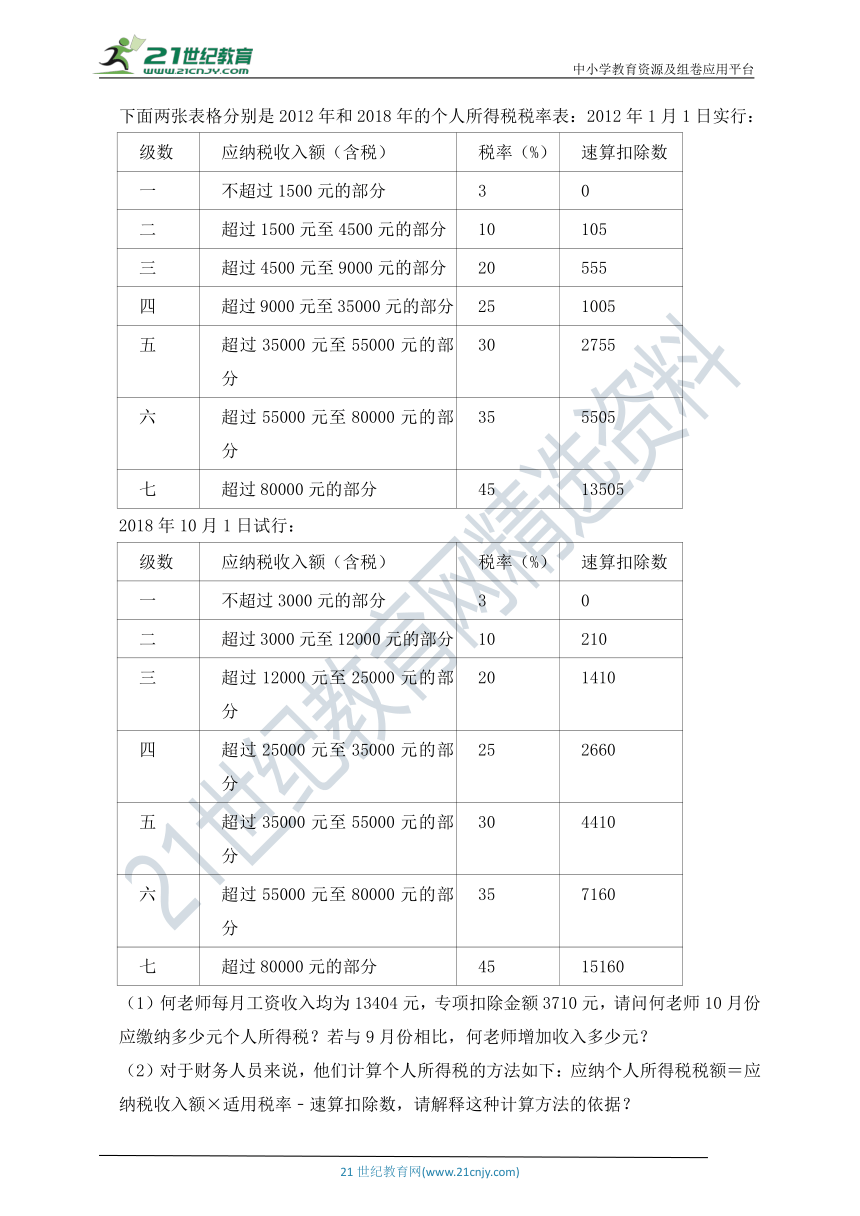
下面两张表格分别是2012年和2018年的个人所得税税率表:2012年1月1日实行:
级数 应纳税收入额(含税) 税率(%) 速算扣除数
一 不超过1500元的部分 3 0
二 超过1500元至4500元的部分 10 105
三 超过4500元至9000元的部分 20 555
四 超过9000元至35000元的部分 25 1005
五 超过35000元至55000元的部分 30 2755
六 超过55000元至80000元的部分 35 5505
七 超过80000元的部分 45 13505
2018年10月1日试行:
级数 应纳税收入额(含税) 税率(%) 速算扣除数
一 不超过3000元的部分 3 0
二 超过3000元至12000元的部分 10 210
三 超过12000元至25000元的部分 20 1410
四 超过25000元至35000元的部分 25 2660
五 超过35000元至55000元的部分 30 4410
六 超过55000元至80000元的部分 35 7160
七 超过80000元的部分 45 15160
(1)何老师每月工资收入均为13404元,专项扣除金额3710元,请问何老师10月份应缴纳多少元个人所得税?若与9月份相比,何老师增加收入多少元?
(2)对于财务人员来说,他们计算个人所得税的方法如下:应纳个人所得税税额=应纳税收入额×适用税率﹣速算扣除数,请解释这种计算方法的依据?
类型二 自建确定性函数模型解决实际问题
例2 某住宅小区为了营造一个优雅、舒适的生活环境,打算建造一个八边形的休闲花园,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成面积为200米2的十字形区域,且计划在正方形MNPK上建一座花坛,其造价为4 200元/米2,在四个相同的矩形上(图中的阴影部分)铺花岗岩路面,其造价为210元/米2,并在四个三角形空地上铺草坪,其造价为80元/米2.
(1)设AD的长为x米,试写出总造价Q(单位:元)关于x的函数解析式;
(2)问:当x取何值时,总造价最少?求出这个最小值.
跟踪训练2 某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.
旅游点规定:每辆自行车的日租金不低于3元并且不超过20元,每辆自行车的日租金x元只取整数,用y表示出租所有自行车的日净收入.(日净收入即一日中出租的所有自行车的总收入减去管理费用后的所得)
(1)求函数y=f(x)的解析式;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
类型三 建立拟合函数模型解决实际问题
例3 某个体经营者把开始六个月试销A,B两种商品的逐月投资金额与所获纯利润列成下表.
投资A种商品金额(万元) 1 2 3 4 5 6
获纯利润(万元) 0.65 1.39 1.85 2 1.84 1.40
投资B种商品金额(万元) 1 2 3 4 5 6
获纯利润(万元) 0.30 0.59 0.88 1.20 1.51 1.79
该经营者准备第七个月投入12万元经营这两种商品,但不知A,B两种商品各投入多少万元才合算,请你帮助制定一个资金投入方案,使得该经营者能获得最大纯利润,并按你的方案求出该经营者第七个月可获得的最大纯利润(结果保留两位有效数字).
答案
例1:1.分段函数:①20≤x≤40;②40≤x≤50;③50≤x≤80;
2.(2)设利润为w,根据题意得:
①当20≤x≤40时,w=20(40x+2000)﹣300×1.6x﹣5000﹣4000=320x+31000,
∵k>0,∴w随x的增大而增大,∴当x=40时,w有最大值为:320×40+31000=43800(元);
②当40≤x≤50时,w=20(30x+2400)﹣300×1.6x﹣5000﹣4000=120x+39000,
∵k>0,∴w随x的增大而增大,∴当x=50时,w有最大值为:120×50+39000=45000(元);
③当50≤x≤80时,w=20(10x+3400)﹣300×1.6x﹣5000﹣4000=﹣280x+59000,
∵k<0,∴w随x的增大而减小,∴当x=50时,w有最大值为:﹣280×50+59000=45000(元);
所以平均每天投入饲料50千克时,该养殖户当年在该鱼糖养殖这种鱼获得的利润最多,最多利润是45000元.
跟踪训练1:解:(1)10月份,13404﹣3710﹣5000=4694,∴3000×3%+1694×10%=259.4;
9月份,13404﹣3710﹣3500=6194,∴1500×3%+3000×10%+1694×20%=683.8;
增加收入683.8﹣259.4=424.4元;
(2)速算扣除数等于按当前级数税率计算后,前面级数多算的金额,所以扣除,
如2018年10月的表中,210=3000×7%,1410=9000×10%+3000×17%,2660=13000×5%+9000×15%+3000×22%,依此类推.
例2:解 (1)设AM=y,AD=x,
则x2+4xy=200,∴y=.
故Q=4 200x2+210×4xy+80×2y2=38 000+4 000x2+(0
且0
∴当t=10时,umin=20.故当x=时,Qmin=118 000(元).
跟踪训练2:
解 (1)当3≤x≤6时,y=50x-115,令50x-115>0,
解得x>2.3.
又因为x∈N,所以3≤x≤6,且x∈N.
当6<x≤20,且x∈N时,
y=[50-3(x-6)]x-115=-3x2+68x-115,
综上可知
y=f(x)=
(2)当3≤x≤6,且x∈N时,因为y=50x-115是增函数,所以当x=6时,ymax=185元.
当6<x≤20,且x∈N时,
y=-3x2+68x-115=-32+,
所以当x=11时,ymax=270元.
综上所述,当每辆自行车日租金定为11元时才能使日净收入最多,为270元.
例3:
解 以投资额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如图所示.
观察散点图可以看出,A种商品所获纯利润y与投资额x之间的变化规律可以用二次函数模型进行模拟,如图①所示.取(4,2)为最高点,则y=a(x-4)2+2(a≠0),再把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15,所以y=-0.15(x-4)2+2.
B种商品所获纯利润y与投资额x之间的变化规律是线性的,可以用一次函数模型进行模拟,如图②所示.
设y=kx+b(k≠0),取点(1,0.30)和(4,1.20)代入,
得解得
所以y=0.3x.
设第七个月投入A,B两种商品的资金分别为x万元,(12-x)万元,总利润为W万元,那么W=yA+yB
=-0.15(x-4)2+2+0.3(12-x),
所以W=-0.15(x-3)2+0.15×9+3.2.
当x=3时,W取最大值,约为4.6万元,此时B商品的投资为9万元.
故该经营者下个月把12万元中的3万元投资A种商品,9万元投资B种商品,可获得最大利润,约为4.6万元.
反思与感悟 在建立和应用函数模型时,准确地把题目要求翻译成数学问题非常重要,另外实际问题要注意实际意义对定义域、取值范围的影响.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
