4.2直线、圆的位置关系课件18张PPT
文档属性
| 名称 | 4.2直线、圆的位置关系课件18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 764.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览



文档简介
课件18张PPT。4.2直线与圆的位置关系 点到直线的距离公式,圆的标准方程和一般方程分别是什么?
1、点到直线的距离公式 :
2、圆的标准方程:
3、圆的一般方程:
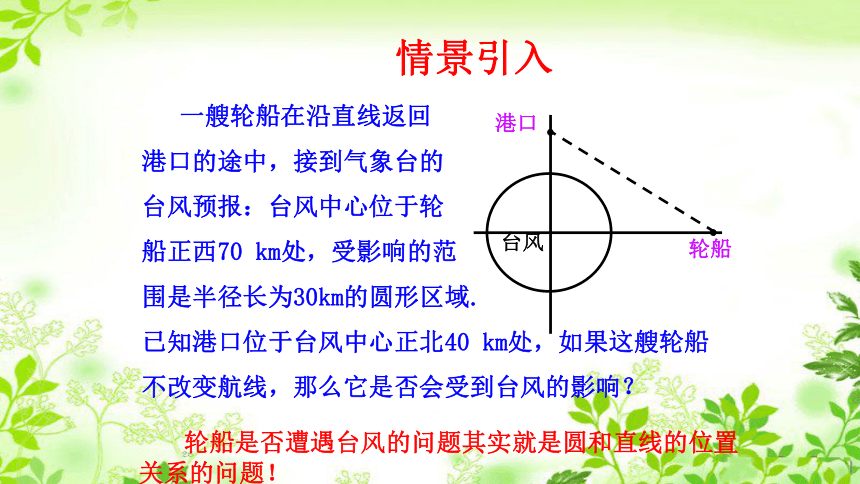
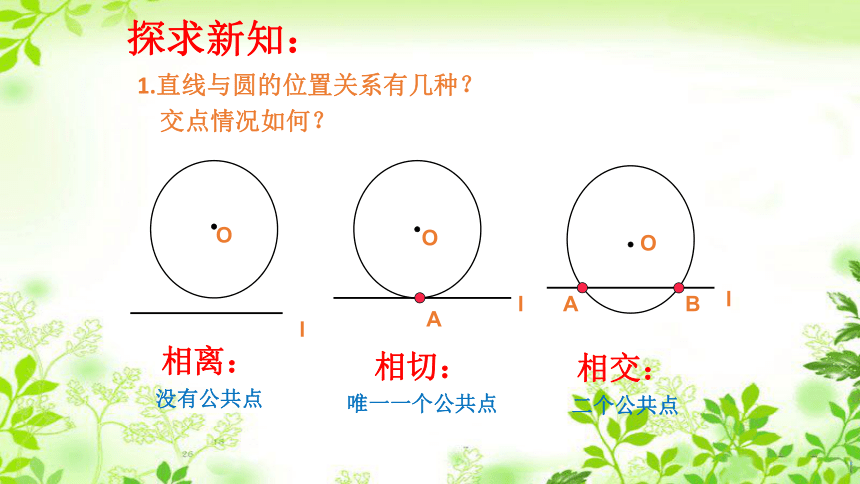
知识回顾 情景引入 轮船是否遭遇台风的问题其实就是圆和直线的位置关系的问题!探求新知:1.直线与圆的位置关系有几种?
交点情况如何?相离:
没有公共点相切:
唯一一个公共点相交:
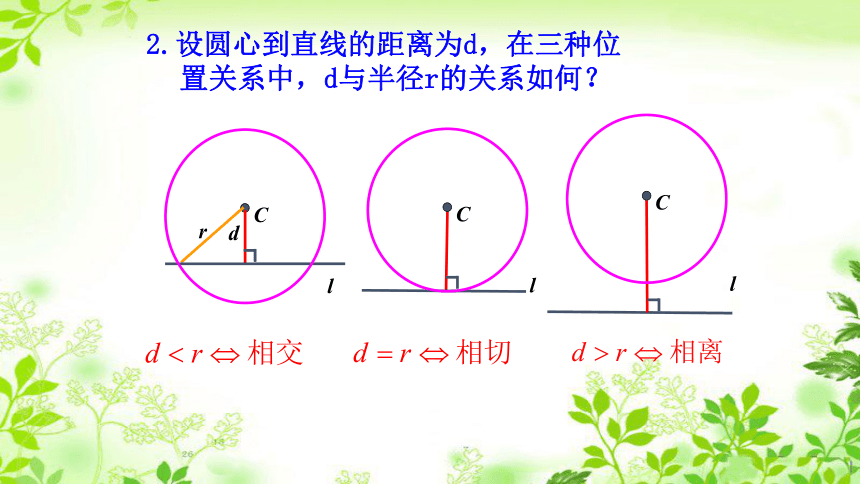
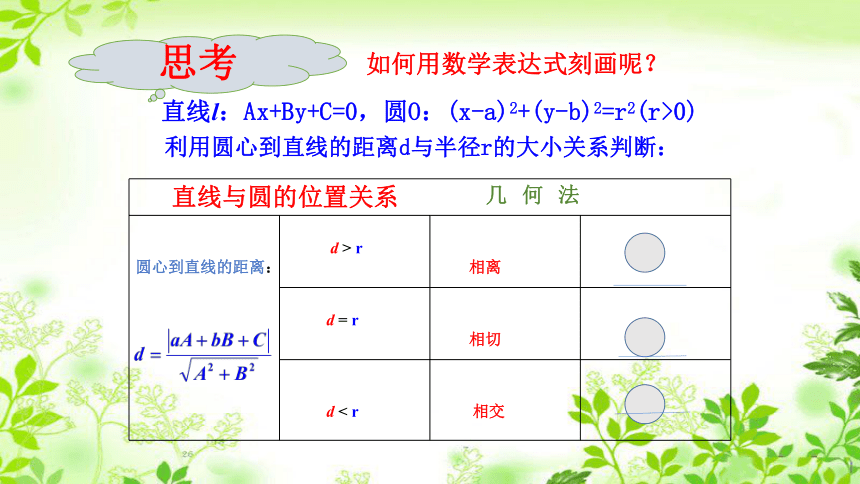
二个公共点思考如何用数学表达式刻画呢?解析法 利用圆心到直线的距离d与半径r的大小关系判断:
思考如何用数学表达式刻画呢? 几 何 法 回归情景所以直线和圆没有公共点解:解析法:
建立直角坐标系如图所示,10km为一个单位长度,所以圆O的方程为 , 直线AB 的方程为 ,所以这个实际问题实际是圆和直线的位置关系问题。
所以直线和圆相离,所以轮船不会遭遇台风。解:几何法
建立直角坐标系如图所示,10km为一个单位长度,所以圆O的方程为 , 直线AB 的方程为 ,所以这个实际问题实际是圆和直线的位置关系问题。
设圆心为O,圆心到直线的距离为d,半径为r,所O(0,0),r=3
直线与圆相离轮船不会遭遇台风解:几何法
设圆心为O,圆心到直线的距离为d
所以,O(0,0),r=3
所以,直线和圆相交判断直线 与圆 的位置关 系是什么?练一练1.判断直线与圆的位置关系常用几何法,其一般步骤分别为:
①把圆的方程化为标准方程,求出圆的圆心坐标和半径r.
②利用点到直线的距离公式求圆心到直线的距离d.
③判断:当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.【提升总结】典例精析解:由题意得,圆心C(1,2)
且P(2,3)在圆上,且线段CP和切线垂直,所以切线的斜率存在解:由题意得,圆心C(1,-2)且点P(2,3)在圆外过P点的切线有两条求过一点P的圆的切线方程问题需注意:1.先判断点P与圆的位置关系2.在求切线的过程中,要注意讨论斜率不存在的情况悄悄告诉你小结:1.2.3.求圆相切的问题,注意点在圆上还是圆外。 注意数形结合思想、方程思想、运动变化观点的综合运用。 作业课后的习题谢 谢
1、点到直线的距离公式 :
2、圆的标准方程:
3、圆的一般方程:
知识回顾 情景引入 轮船是否遭遇台风的问题其实就是圆和直线的位置关系的问题!探求新知:1.直线与圆的位置关系有几种?
交点情况如何?相离:
没有公共点相切:
唯一一个公共点相交:
二个公共点思考如何用数学表达式刻画呢?解析法 利用圆心到直线的距离d与半径r的大小关系判断:
思考如何用数学表达式刻画呢? 几 何 法 回归情景所以直线和圆没有公共点解:解析法:
建立直角坐标系如图所示,10km为一个单位长度,所以圆O的方程为 , 直线AB 的方程为 ,所以这个实际问题实际是圆和直线的位置关系问题。
所以直线和圆相离,所以轮船不会遭遇台风。解:几何法
建立直角坐标系如图所示,10km为一个单位长度,所以圆O的方程为 , 直线AB 的方程为 ,所以这个实际问题实际是圆和直线的位置关系问题。
设圆心为O,圆心到直线的距离为d,半径为r,所O(0,0),r=3
直线与圆相离轮船不会遭遇台风解:几何法
设圆心为O,圆心到直线的距离为d
所以,O(0,0),r=3
所以,直线和圆相交判断直线 与圆 的位置关 系是什么?练一练1.判断直线与圆的位置关系常用几何法,其一般步骤分别为:
①把圆的方程化为标准方程,求出圆的圆心坐标和半径r.
②利用点到直线的距离公式求圆心到直线的距离d.
③判断:当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.【提升总结】典例精析解:由题意得,圆心C(1,2)
且P(2,3)在圆上,且线段CP和切线垂直,所以切线的斜率存在解:由题意得,圆心C(1,-2)且点P(2,3)在圆外过P点的切线有两条求过一点P的圆的切线方程问题需注意:1.先判断点P与圆的位置关系2.在求切线的过程中,要注意讨论斜率不存在的情况悄悄告诉你小结:1.2.3.求圆相切的问题,注意点在圆上还是圆外。 注意数形结合思想、方程思想、运动变化观点的综合运用。 作业课后的习题谢 谢
