4.1.1 圆的标准方程课件20张PPT
文档属性
| 名称 | 4.1.1 圆的标准方程课件20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 21:30:09 | ||
图片预览






文档简介
课件20张PPT。4.1 圆的方程第四章4.1.1 圆的标准方程 学习目标
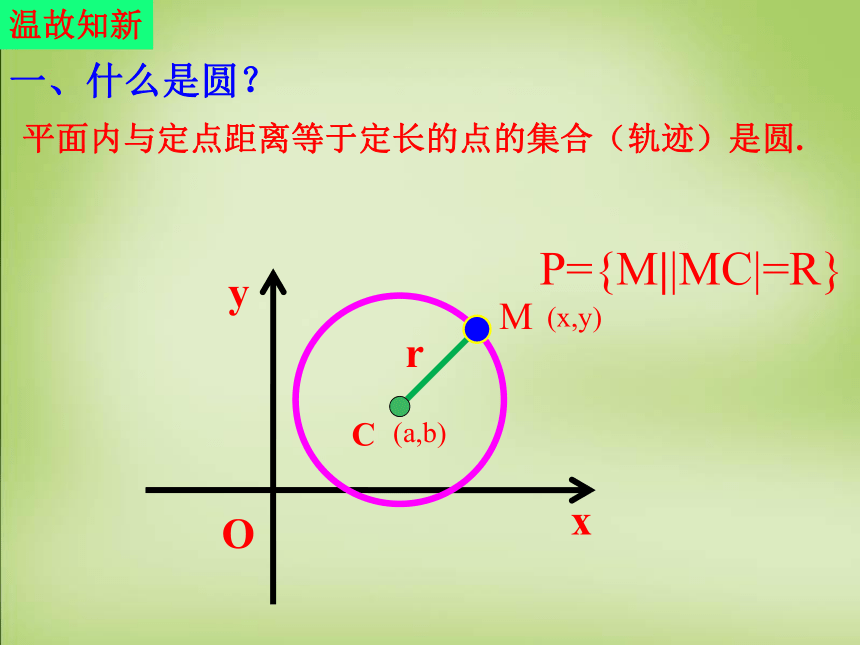
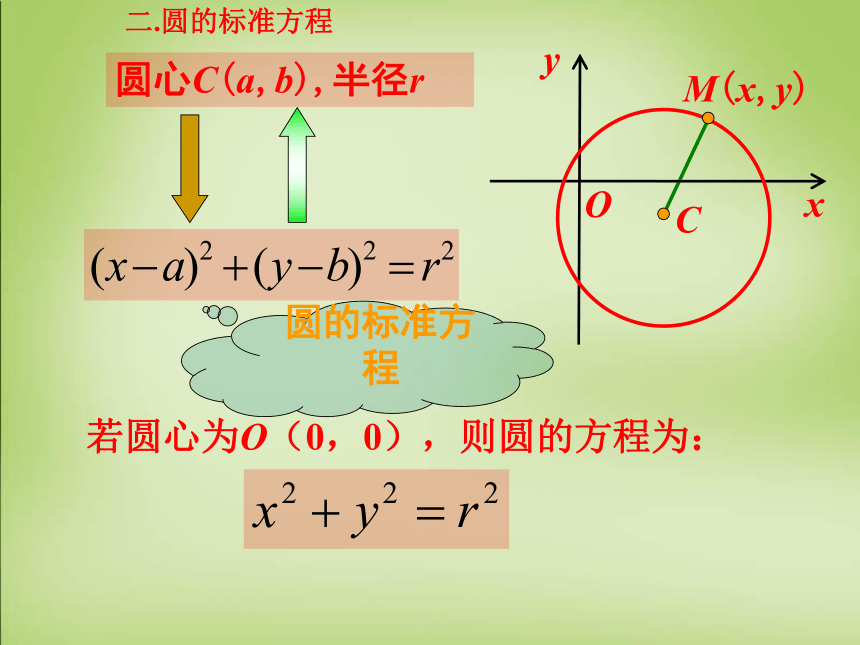
1. 初步理解圆的标准方程,能根据圆心、半径熟练写出圆的标准方程,并能够根据圆的标准方程熟练求出其圆心坐标和半径。2. 学会判断点与圆的位置关系。3. 会用待定系数法求圆的标准方程。 (a,b)C温故知新MrP={M||MC|=R}一、什么是圆?平面内与定点距离等于定长的点的集合(轨迹)是圆.(x,y)xyOCM(x,y)圆心C(a,b),半径r若圆心为O(0,0),则圆的方程为:圆的标准方程
二.圆的标准方程例1 写出圆心为(3,4),半径为5的圆的方程,并判定点A(0,0),B(1,3)是否在这个圆上.
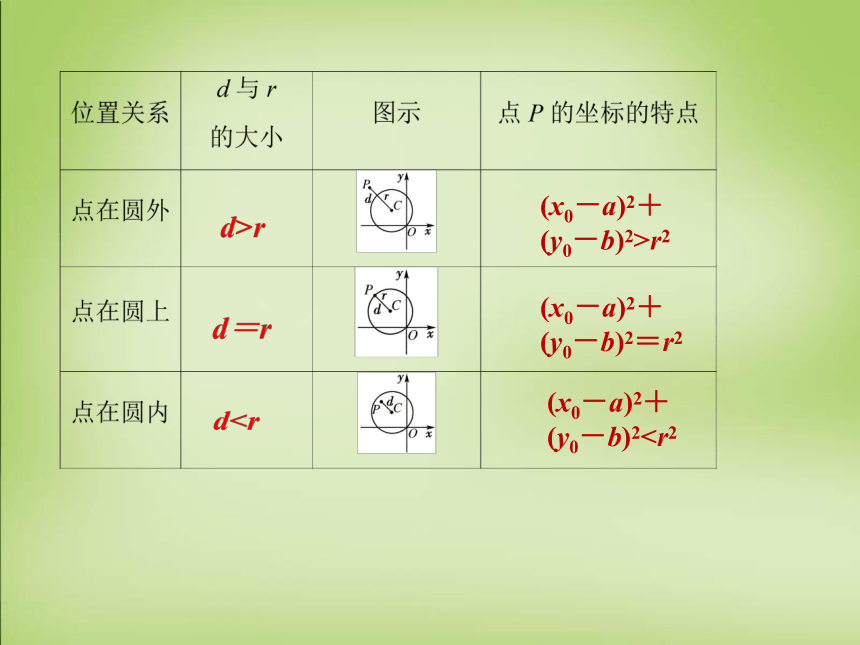
(x0-a)2+
(y0-b)2>r2 (x0-a)2+
(y0-b)2=r2 (x0-a)2+
(y0-b)2练习1 点P(1,-1)在圆(x+2)2+y2=m的外部,则实数m的取值范围是________.
圆的标准方程的综合应用●探索延拓 △ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求△ABC的外接圆的标准方程.例2:A(5,1)EDPC(2,-8)B(7,-3)yxR几何方法L1L2O(1)待定系数法.
由于圆的标准方程中含有a,b,r三个参数,必须具备三个独立条件,才能求出一个圆的标准方程,用待定系数法求圆的方程,即列出关于a,b,r的方程组,解方程组求a,b,r.一般步骤如下:①设出所求的圆的标准方程(x-a)2+(y-b)2=r2;
②根据已知条件,建立关于a,b,r的方程组;
③解方程组时,求出a,b,r的值,并把它们代入所设的方程中,就得到所求圆的标准方程. 规律总结:求圆的标准方程有以下两种方法:(2)几何法.
通过研究已知条件,结合圆的几何性质,求得圆的基本量(圆心坐标,半径长),进而求得方程.
圆的常用的几何性质:①圆的弦的垂直平分线过圆心;②两条弦的垂直平分线的交点为圆心;
1.方程(x-a)2+(y-b)2=0表示的图形是( )
A.以(a,b)为圆心的圆
B.以(-a,-b)为圆心的圆
C.点(a,b)
D.点(-a,-b)
[答案] C3. △ABC的三个顶点的坐标是A(4,0),B(0,3),C(0,0),求它的外接圆的标准方程.小结1.圆的标准方程
圆心是(a,b),半径是r的圆的标准方程
2.点与圆的位置关系(x-a)2+(y-b)2=r2一、知识内容课堂小结作业 :
课本121页 练习4
大本59页 思考题1再见谢谢观赏
1. 初步理解圆的标准方程,能根据圆心、半径熟练写出圆的标准方程,并能够根据圆的标准方程熟练求出其圆心坐标和半径。2. 学会判断点与圆的位置关系。3. 会用待定系数法求圆的标准方程。 (a,b)C温故知新MrP={M||MC|=R}一、什么是圆?平面内与定点距离等于定长的点的集合(轨迹)是圆.(x,y)xyOCM(x,y)圆心C(a,b),半径r若圆心为O(0,0),则圆的方程为:圆的标准方程
二.圆的标准方程例1 写出圆心为(3,4),半径为5的圆的方程,并判定点A(0,0),B(1,3)是否在这个圆上.
(x0-a)2+
(y0-b)2>r2 (x0-a)2+
(y0-b)2=r2 (x0-a)2+
(y0-b)2
圆的标准方程的综合应用●探索延拓 △ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求△ABC的外接圆的标准方程.例2:A(5,1)EDPC(2,-8)B(7,-3)yxR几何方法L1L2O(1)待定系数法.
由于圆的标准方程中含有a,b,r三个参数,必须具备三个独立条件,才能求出一个圆的标准方程,用待定系数法求圆的方程,即列出关于a,b,r的方程组,解方程组求a,b,r.一般步骤如下:①设出所求的圆的标准方程(x-a)2+(y-b)2=r2;
②根据已知条件,建立关于a,b,r的方程组;
③解方程组时,求出a,b,r的值,并把它们代入所设的方程中,就得到所求圆的标准方程. 规律总结:求圆的标准方程有以下两种方法:(2)几何法.
通过研究已知条件,结合圆的几何性质,求得圆的基本量(圆心坐标,半径长),进而求得方程.
圆的常用的几何性质:①圆的弦的垂直平分线过圆心;②两条弦的垂直平分线的交点为圆心;
1.方程(x-a)2+(y-b)2=0表示的图形是( )
A.以(a,b)为圆心的圆
B.以(-a,-b)为圆心的圆
C.点(a,b)
D.点(-a,-b)
[答案] C3. △ABC的三个顶点的坐标是A(4,0),B(0,3),C(0,0),求它的外接圆的标准方程.小结1.圆的标准方程
圆心是(a,b),半径是r的圆的标准方程
2.点与圆的位置关系(x-a)2+(y-b)2=r2一、知识内容课堂小结作业 :
课本121页 练习4
大本59页 思考题1再见谢谢观赏
