人教新课标A版 必修2 第三章 探究与发现 魔术师的地毯课件16张PPT
文档属性
| 名称 | 人教新课标A版 必修2 第三章 探究与发现 魔术师的地毯课件16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览




文档简介
课件16张PPT。魔术师的地毯 一天,著名魔术大师秋先生拿了一块长和宽都是1.3米的地毯去找地毯匠敬师傅,要求把这块正方形的地毯改制成宽0.8米,长2.1米的矩形地毯。 敬师傅对秋先生说:“你这位大名鼎鼎的魔术师,难道连小学算术都没有学过吗?边长为1.3米的正方形面积是1.69平方米,而宽为0.8米,长为2.1米的矩形面积只有1.68平方米,两者并不相等啊!除非裁去0.01平方米,不然没法做。”秋先生拿出他事先画好的两张设计图,对敬师傅说:“你先照这张图的尺寸把地毯裁成四块,然后再照另一张图的样子把这四块拼在一起缝好就行了。魔术大师是从来不会出错的,你只管放心做吧!”敬师傅照着秋先生给的图纸做了,缝好一量,果真是宽0.8米,长2.1米,魔术师拿着改好的地毯得意洋洋地走了。而敬师傅还在纳闷呢,这是怎么回事呢?
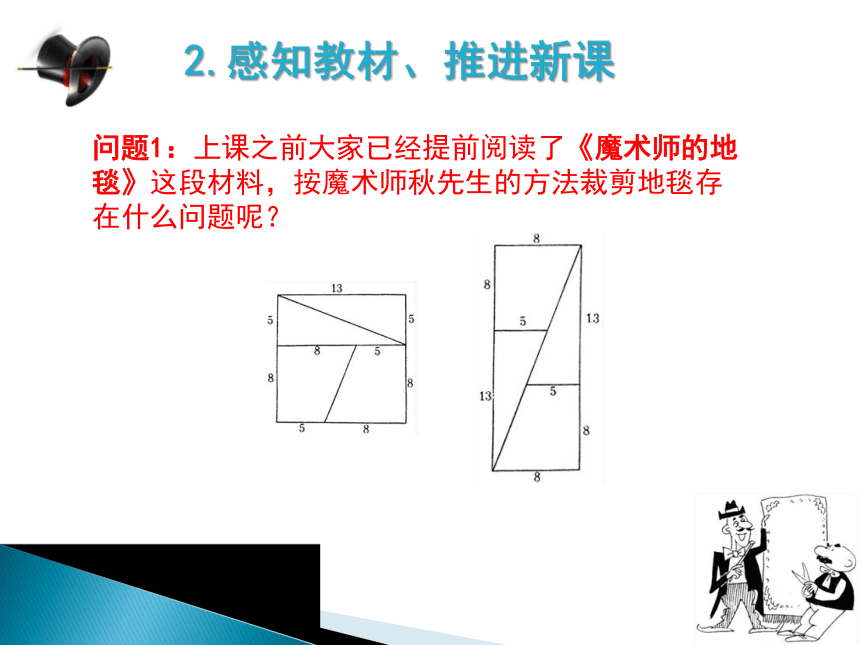
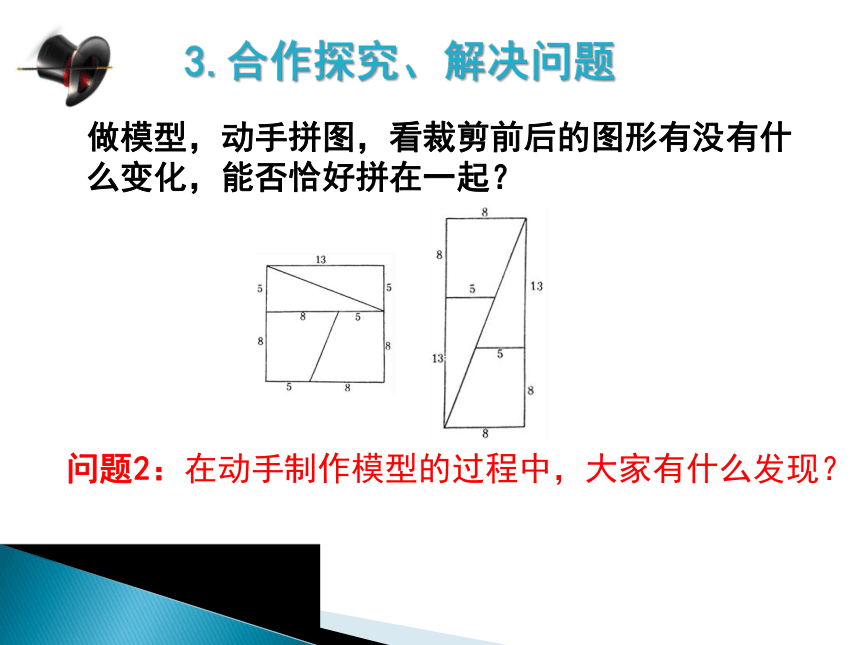
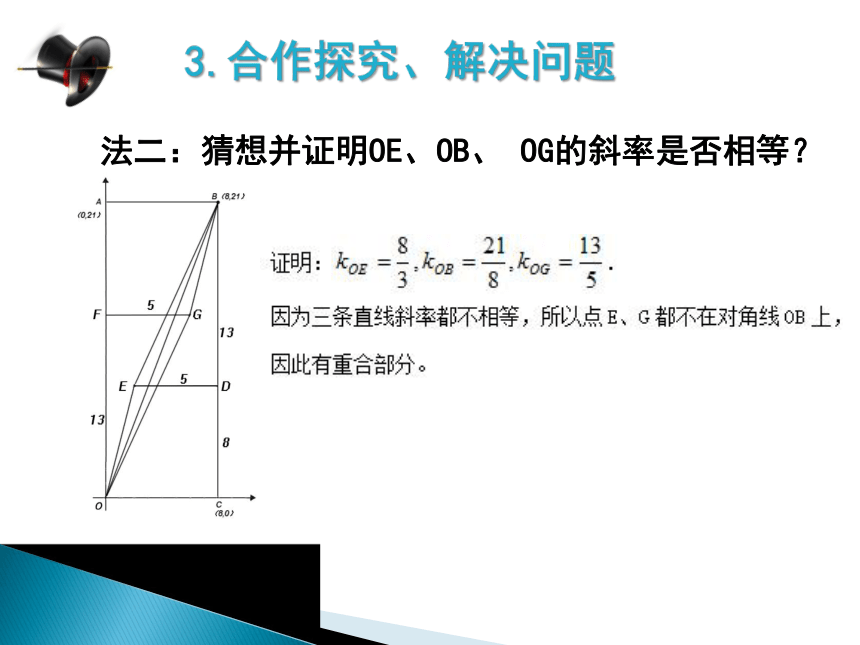
2.感知教材、推进新课2.感知教材、推进新课问题1:上课之前大家已经提前阅读了《魔术师的地毯》这段材料,按魔术师秋先生的方法裁剪地毯存在什么问题呢?3.合作探究、解决问题做模型,动手拼图,看裁剪前后的图形有没有什么变化,能否恰好拼在一起?问题2:在动手制作模型的过程中,大家有什么发现?3.合作探究、解决问题法一:判断点E、点G、是否在直线OB上并证明.法二:猜想并证明OE、OB、 OG的斜率是否相等?问题3:请大家用学过的知识帮敬师傅解开这个谜,思考有哪些数学的方法可以解决这个问题?
3.合作探究、解决问题法一:判断点E、点G、是否在直线OB上并证明.3.合作探究、解决问题法二:猜想并证明OE、OB、 OG的斜率是否相等?3.合作探究、解决问题问题4:既然裁剪拼接前后图形面积不相等,那么少的那一部分是什么图形?怎么证明你的猜想?3.合作探究、解决问题问题5:你能用数学的方法把重合部分的面积精确地计算出来吗?5.模型改进、发现完美通过我们的探究发现,前面我们一起表演的魔术是不够完美的,原因是很容易让别人看出破绽——空隙或重叠.问题6:在此基础上,按照秋先生的想法,使用如图的形式如何裁剪才是完美的呢?
发现:把正方形按照黄金分割就可以使魔术的效果达到完美,而不是趋于完美!问题6:在此基础上,按照秋先生的想法,使用如图的形式如何裁剪才是完美的呢?
5.模型改进、发现完美黄金分割在自然界中的完美展现 动物界,形体优美的动物形体,如马,骡、狮、虎、豹、犬等,凡看上去健美的,其身体部分长与宽的比例也大体上接近于黄金分割如:蝴蝶身长与双翅展开后的长度之比也接近0.618。黄金分割在建筑中的完美展现 法国巴黎埃菲尔铁塔 、纽约联合国大厦、胡夫金字塔、古代雅典的巴特农神殿 6.师生畅谈、课堂小结(1)感受到魔术的美妙,意识到不要迷信于事物的表象,要透过现象认识事物的本质(2)加深了对坐标法的印象,意识到用坐标法解决问题是一种重要的数学手段。(3)感受到黄金分割所蕴含的数学美学。(4)从观察、发现、猜想到论证、反思、拓展的探究过程. 数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。——高斯课后寄语: 给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
——高斯巩固训练:1.将一个边长为3的正方形按下图剪裁,能否拼接成如图的长方形?2.将一个边长为8的正方形按下图剪裁,能否拼接成如图的长方形?1235135225
2.感知教材、推进新课2.感知教材、推进新课问题1:上课之前大家已经提前阅读了《魔术师的地毯》这段材料,按魔术师秋先生的方法裁剪地毯存在什么问题呢?3.合作探究、解决问题做模型,动手拼图,看裁剪前后的图形有没有什么变化,能否恰好拼在一起?问题2:在动手制作模型的过程中,大家有什么发现?3.合作探究、解决问题法一:判断点E、点G、是否在直线OB上并证明.法二:猜想并证明OE、OB、 OG的斜率是否相等?问题3:请大家用学过的知识帮敬师傅解开这个谜,思考有哪些数学的方法可以解决这个问题?
3.合作探究、解决问题法一:判断点E、点G、是否在直线OB上并证明.3.合作探究、解决问题法二:猜想并证明OE、OB、 OG的斜率是否相等?3.合作探究、解决问题问题4:既然裁剪拼接前后图形面积不相等,那么少的那一部分是什么图形?怎么证明你的猜想?3.合作探究、解决问题问题5:你能用数学的方法把重合部分的面积精确地计算出来吗?5.模型改进、发现完美通过我们的探究发现,前面我们一起表演的魔术是不够完美的,原因是很容易让别人看出破绽——空隙或重叠.问题6:在此基础上,按照秋先生的想法,使用如图的形式如何裁剪才是完美的呢?
发现:把正方形按照黄金分割就可以使魔术的效果达到完美,而不是趋于完美!问题6:在此基础上,按照秋先生的想法,使用如图的形式如何裁剪才是完美的呢?
5.模型改进、发现完美黄金分割在自然界中的完美展现 动物界,形体优美的动物形体,如马,骡、狮、虎、豹、犬等,凡看上去健美的,其身体部分长与宽的比例也大体上接近于黄金分割如:蝴蝶身长与双翅展开后的长度之比也接近0.618。黄金分割在建筑中的完美展现 法国巴黎埃菲尔铁塔 、纽约联合国大厦、胡夫金字塔、古代雅典的巴特农神殿 6.师生畅谈、课堂小结(1)感受到魔术的美妙,意识到不要迷信于事物的表象,要透过现象认识事物的本质(2)加深了对坐标法的印象,意识到用坐标法解决问题是一种重要的数学手段。(3)感受到黄金分割所蕴含的数学美学。(4)从观察、发现、猜想到论证、反思、拓展的探究过程. 数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。——高斯课后寄语: 给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
——高斯巩固训练:1.将一个边长为3的正方形按下图剪裁,能否拼接成如图的长方形?2.将一个边长为8的正方形按下图剪裁,能否拼接成如图的长方形?1235135225
