3.3.2 两点间的距离课件16张PPT
文档属性
| 名称 | 3.3.2 两点间的距离课件16张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 21:35:06 | ||
图片预览



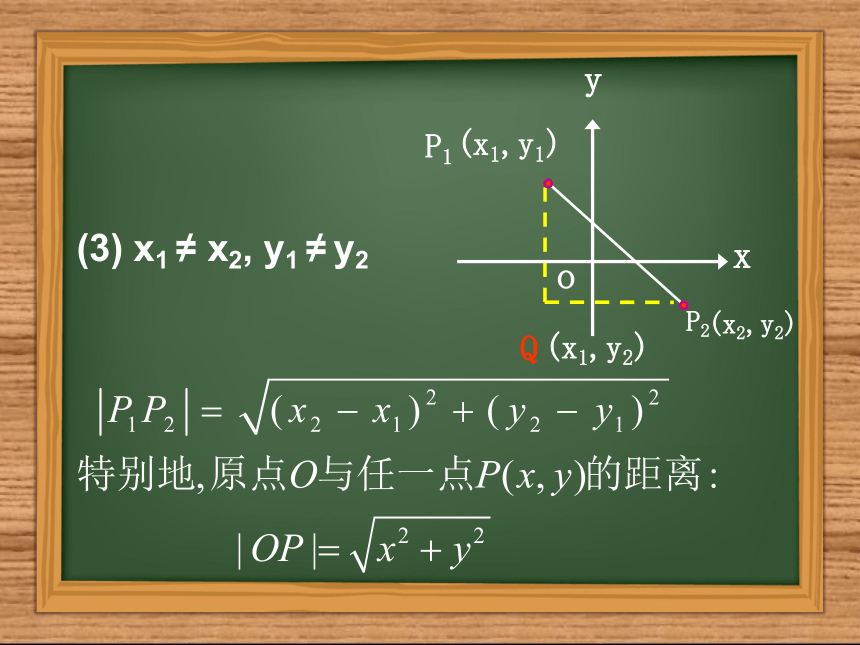



文档简介
课件16张PPT。数 学 组 3.3.2 两点间的距离 已知平面上两点P1(x1,y1),P2(x2,y2),如何求P1P2的距离|P1P2|呢?yxoP1P2yxoP2P1(1) x1≠x2, y1=y2(2) x1 = x2, y1 ≠ y2yxoAB思考Q(x1,y2)(3) x1 ≠ x2, y1 ≠ y2练习1 已知三角形ABC的三个顶点A(1,4),
B(4,1),C(5,5),判断三角形的形状。例1:例2、证明平行四边形四条边的平方和等于两条对角线的平方和。分析:坐标法通过建立平面直角坐标系,用代数方法
解决几何问题的方法,称为坐标法。例2、证明平行四边形四条边的平方和等于两条对角线的平方和。(b,c)(a+b,c)(a,0)(0,0) 证明直角三角形斜边的中点到三个顶点的距离相等。(0,0)(a,0)(0,b)学以致用2: 设P为矩形ABCD所在平面上任意
一点,求证:
|PA|2+ |PC|2= |PB|2+ |PD|2。学以致用3: 平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是:收获1收获2 一种方法:坐标法 一种思想:转化思想。将几何问题转化为代数问题 一个公式:两点间距离公式2017年5月
B(4,1),C(5,5),判断三角形的形状。例1:例2、证明平行四边形四条边的平方和等于两条对角线的平方和。分析:坐标法通过建立平面直角坐标系,用代数方法
解决几何问题的方法,称为坐标法。例2、证明平行四边形四条边的平方和等于两条对角线的平方和。(b,c)(a+b,c)(a,0)(0,0) 证明直角三角形斜边的中点到三个顶点的距离相等。(0,0)(a,0)(0,b)学以致用2: 设P为矩形ABCD所在平面上任意
一点,求证:
|PA|2+ |PC|2= |PB|2+ |PD|2。学以致用3: 平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是:收获1收获2 一种方法:坐标法 一种思想:转化思想。将几何问题转化为代数问题 一个公式:两点间距离公式2017年5月
