3.1.1 倾斜角与斜率课件33张PPT
文档属性
| 名称 | 3.1.1 倾斜角与斜率课件33张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 917.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-29 00:00:00 | ||
图片预览








文档简介
课件33张PPT。第三章 直线与方程
3.1.1 直线的倾斜角与斜率一天,著名魔术大师秋先生拿了一块长和宽都是1.3米的地毯去找地毯匠敬师傅,要求把这块正方形地毯改成0.8米宽2.1米长的矩形.敬师傅对秋先生说:“你这位大名鼎鼎的魔术师,难道连小学算术都没有学过吗?边长1.3米的正方形面积为1.69平方米,而宽0.8米长2.1米的矩形面积只有1.68平方米,两者并不相等啊!除非裁去0.01平方米,不然没法做.”秋先生拿出他事先画好的两张设计图,对敬师傅说:“你先照这张图(图2)的尺寸把地毯裁成四块,然后照另一张图(图3)的样子把这四块拼在一起缝好就行了.魔术大师是从来不会错的,你放心做吧!”敬师傅照着做了,缝好一量,果真是宽0.8米长2.1米.魔术师拿着改好的地毯满意地走了,而敬师傅却还在纳闷儿:这是怎么回事呢?那0.01平方米的地毯到什么地方去了?你能帮敬师傅解开这个谜吗? 解析几何的背景 文艺复兴使欧洲学者继承了古希腊的几何学,也接受了东方传入的代数学。
以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算来研究几何图形性质的方法,叫坐标法. 用坐标法研究几何的学科
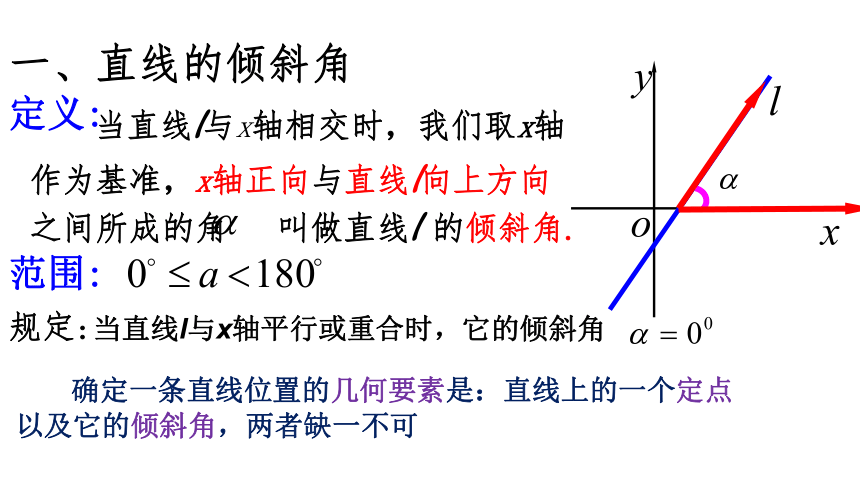
称为解析几何. 倾斜角的定义?在平面直角坐标系中一条直线的位置由哪些条件确定?斜率的定义?有什么限制条件?一、直线的倾斜角定义: 当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线l 的倾斜角.范围: 确定一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角,两者缺一不可 二、直线的斜率定义:斜率不存在课前检测题:已知下列直线的倾斜角,求直线的斜率.问题1:直线的倾斜角与斜率之间的关系?直线倾斜角越大,斜率就越大吗?(小组1)小组合作探究活动(展示成果5分钟)问题2:已知下列直线的倾斜角范围,你能求出直线斜率的范围吗?(小组2)问题3:直线的斜率可以用直线上两点
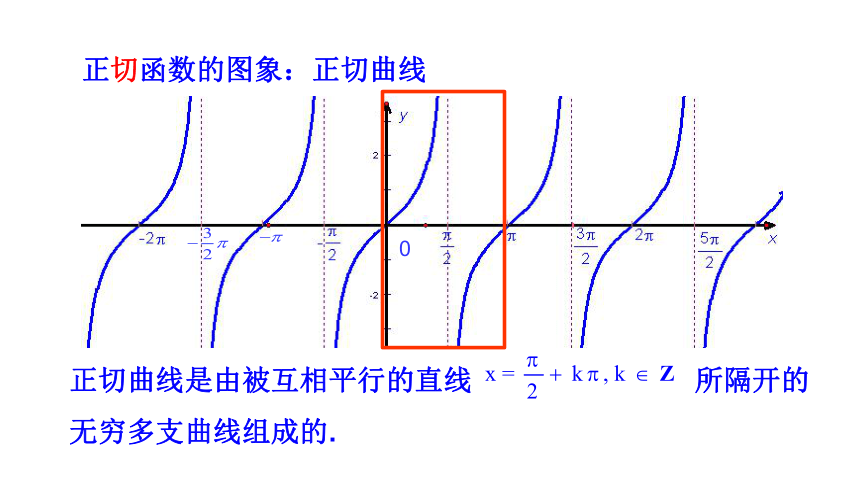
的坐标来表示吗?(小组3)问题4:用本节课学习的知识解这个谜吗?(小组4)问题1:直线的倾斜角与斜率之间的关系?直线倾斜角越大,斜率就越大吗?(小组1)小组合作探究活动几何画板正切函数的图象:正切曲线课堂检测1:问题2:已知下列直线的倾斜角范围,你能求出直线斜率的范围吗?(小组2) 小组合作探究活动几何画板课堂检测2:小组合作探究活动问题3:直线的斜率可以用直线上两点
的坐标来表示吗?(小组3)探究3:两点确定一条直线,直线确定,倾斜角也就确定,斜率也就确定了,那么直线的斜率可以用直线上两点
(其 中x1≠x2)的坐标来表示吗?
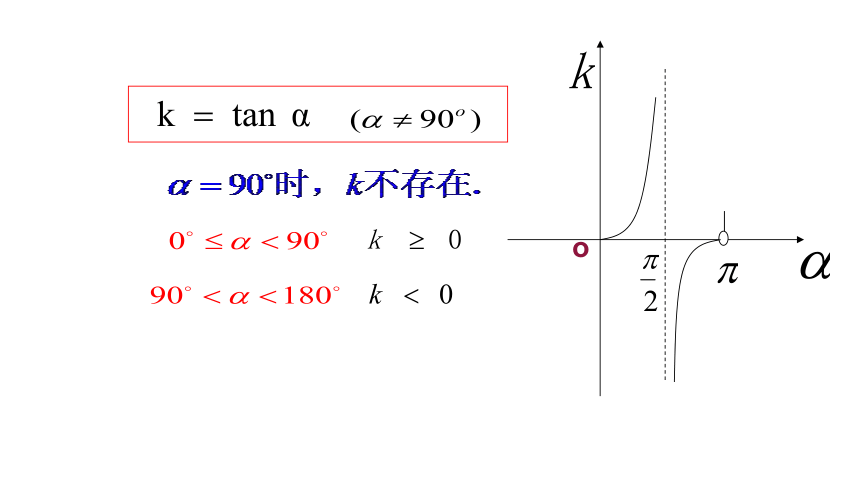
当倾斜角是锐角时 当倾斜角是钝角时 ∴当α为锐角时 当倾斜角是锐角时 如何由直线上两点的坐标计算直线的斜率:当α为钝角时 当倾斜角是钝角时 三、直线的斜率公式思考:上述公式与直线上这两点坐标的顺序有关系吗?无关当直线P1P2平行于x轴,或与x轴重合时,
还适用吗?为什么?O适用思考:O当直线平行于y轴,或与y轴重合时,公式还适用吗?不适用,因为分母为0.斜率不存在.思考:求经过下列两点的直线的斜率,并判断其倾斜角是锐角
还是钝角.
(1)C(18,8),D(4,-4); (2)P(0,0),Q(-1, ).课堂检测3:问题4:你能用本节课学习的知识解这个谜吗?(小组4) 小组合作探究活动yO●E
●B问:O、E、B三点共线吗?点拨:
计算判断kOE、kEB是否相等 请用本节课学习的知识解这个谜科学依据、揭示谜底数缺形时少直观
形少数时难入微你能说说本节课的收获吗?(3)从倾斜角(形)能刻画直线的倾斜程度,到斜率(数)也能刻画直线的倾斜程度,这个过程 中主要体现了什么数学思想?(1)在本节课中,你学到了哪些新的概念?他们之间有什么关系?(2)求直线斜率的方法?小结:1.直线倾斜角的定义及其范围:2.斜率k与倾斜角 之间的关系:3.斜率公式:“几何问题代数化”、“数形结合”的思想 斜率k为正,倾斜角为锐角;
斜率k,为负,倾斜角为钝角;
斜率k为0,倾斜角为0°;
斜率k不存在时,倾斜角为直角.小结:高考链接:几何画板进阶作业: 祝:同学们学习愉快! 谢 谢!
以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算来研究几何图形性质的方法,叫坐标法. 用坐标法研究几何的学科
称为解析几何. 倾斜角的定义?在平面直角坐标系中一条直线的位置由哪些条件确定?斜率的定义?有什么限制条件?一、直线的倾斜角定义: 当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角 叫做直线l 的倾斜角.范围: 确定一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角,两者缺一不可 二、直线的斜率定义:斜率不存在课前检测题:已知下列直线的倾斜角,求直线的斜率.问题1:直线的倾斜角与斜率之间的关系?直线倾斜角越大,斜率就越大吗?(小组1)小组合作探究活动(展示成果5分钟)问题2:已知下列直线的倾斜角范围,你能求出直线斜率的范围吗?(小组2)问题3:直线的斜率可以用直线上两点
的坐标来表示吗?(小组3)问题4:用本节课学习的知识解这个谜吗?(小组4)问题1:直线的倾斜角与斜率之间的关系?直线倾斜角越大,斜率就越大吗?(小组1)小组合作探究活动几何画板正切函数的图象:正切曲线课堂检测1:问题2:已知下列直线的倾斜角范围,你能求出直线斜率的范围吗?(小组2) 小组合作探究活动几何画板课堂检测2:小组合作探究活动问题3:直线的斜率可以用直线上两点
的坐标来表示吗?(小组3)探究3:两点确定一条直线,直线确定,倾斜角也就确定,斜率也就确定了,那么直线的斜率可以用直线上两点
(其 中x1≠x2)的坐标来表示吗?
当倾斜角是锐角时 当倾斜角是钝角时 ∴当α为锐角时 当倾斜角是锐角时 如何由直线上两点的坐标计算直线的斜率:当α为钝角时 当倾斜角是钝角时 三、直线的斜率公式思考:上述公式与直线上这两点坐标的顺序有关系吗?无关当直线P1P2平行于x轴,或与x轴重合时,
还适用吗?为什么?O适用思考:O当直线平行于y轴,或与y轴重合时,公式还适用吗?不适用,因为分母为0.斜率不存在.思考:求经过下列两点的直线的斜率,并判断其倾斜角是锐角
还是钝角.
(1)C(18,8),D(4,-4); (2)P(0,0),Q(-1, ).课堂检测3:问题4:你能用本节课学习的知识解这个谜吗?(小组4) 小组合作探究活动yO●E
●B问:O、E、B三点共线吗?点拨:
计算判断kOE、kEB是否相等 请用本节课学习的知识解这个谜科学依据、揭示谜底数缺形时少直观
形少数时难入微你能说说本节课的收获吗?(3)从倾斜角(形)能刻画直线的倾斜程度,到斜率(数)也能刻画直线的倾斜程度,这个过程 中主要体现了什么数学思想?(1)在本节课中,你学到了哪些新的概念?他们之间有什么关系?(2)求直线斜率的方法?小结:1.直线倾斜角的定义及其范围:2.斜率k与倾斜角 之间的关系:3.斜率公式:“几何问题代数化”、“数形结合”的思想 斜率k为正,倾斜角为锐角;
斜率k,为负,倾斜角为钝角;
斜率k为0,倾斜角为0°;
斜率k不存在时,倾斜角为直角.小结:高考链接:几何画板进阶作业: 祝:同学们学习愉快! 谢 谢!
