人教版数学初中九年级上册知识讲解,巩固练习(教学资料,补习资料):专题23.2 中心对称 23.3 课题学习 图案设计(含答案)
文档属性
| 名称 | 人教版数学初中九年级上册知识讲解,巩固练习(教学资料,补习资料):专题23.2 中心对称 23.3 课题学习 图案设计(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 695.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-30 00:00:00 | ||
图片预览



文档简介
知识
1.中心对称:
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心).
2.轴对称与中心对称的区别
轴对称:两个图形关于一条直线对称,沿该直线翻折,两图形重合;关于一条直线对称的两个图形,对应点的连线被对称轴垂直平分.
中心对称:两个图形关于一点对称,沿该点旋转180°,两个图形重合,关于一点对称的两个图形,对应点的连线被对称中心平分.
3.关于中心对称的图形的性质
(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分;
(2)关于中心对称的两个图形对应线段平行(或在同一条直线上)且相等;
(3)关于中心对称的两个图形是全等图形.
4.确定对称中心的方法
(1)连接任意一对对称点,取这条线段的中点,则该点是对称中心.
(2)连接任意两对对称点,这两条线段的交点即是对称中心.
5.利用尺规作关于中心对称的图形
这类问题应首先明确对称中心的位置,再利用“对应点的连线被对称中心平分”的特性,分别找出原图形中各个关键点的对应点,最后按原图形中各点的次序,将各对应点连接起来.
6.中点对称图形
把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是对称中心.
7.关于原点对称的点的坐标特征
两个点关于原点对称时,它们的坐标符合相反,即点P(x,y)关于原点的对称点为P′(–x,–y).
8.图案设计
图案的设计与日常生活息息相关,通常是利用基本图形的变换来完成设计工作.图形之间基本变换关系有轴对称、平移、旋转这三种基本形式,也有很多图形的形成是经过n次变换复合而成的,其复合形式灵活多样,我们可以根据各自的审美情趣,创造出各种各样的图案.
9.利用基本图案进行组合设计
几个基本图案组合在一起,可能形成一个复合型图案,我们还可以进行多次变换,设计出较大型美丽图案.
重点
重点
中心对称和中心对称图形的定义
关于原点对称的点的坐标特征
难点
中心对称与中心对称图形的区别
易错
区分中心对称与中心对称图形
一、中心对称与中心对称图形
1.中心对称是指两个图形间的位置关系.
2.中心对称是特殊的旋转,旋转角为180°.
3.成中心对称的两个图形,只有一个对称中心,这个对称中心可能在每个图形的外部,也可能在每个图形的内部或图形上,但对称点一定在对称中心的两侧与对称中心重合.
【例1】下列说法中错误的是
A.成中心对称的两个图形全等
B.成中心对称的两个图形中,对称点的连线被对称轴平分
C.中心对称图形的对称中心是对称点连线的中心
D.中心对称图形绕对称中心旋转180°后,都能与自身重合
【答案】B
【解析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与另一个图形重合,那么就说明这两个图形的形状关于这个点成中心对称,中心对称图形的对称中心是对称点连线的交点,根据中心对称图形的定义和性质可知A、C、D正确,B错误.故选B.
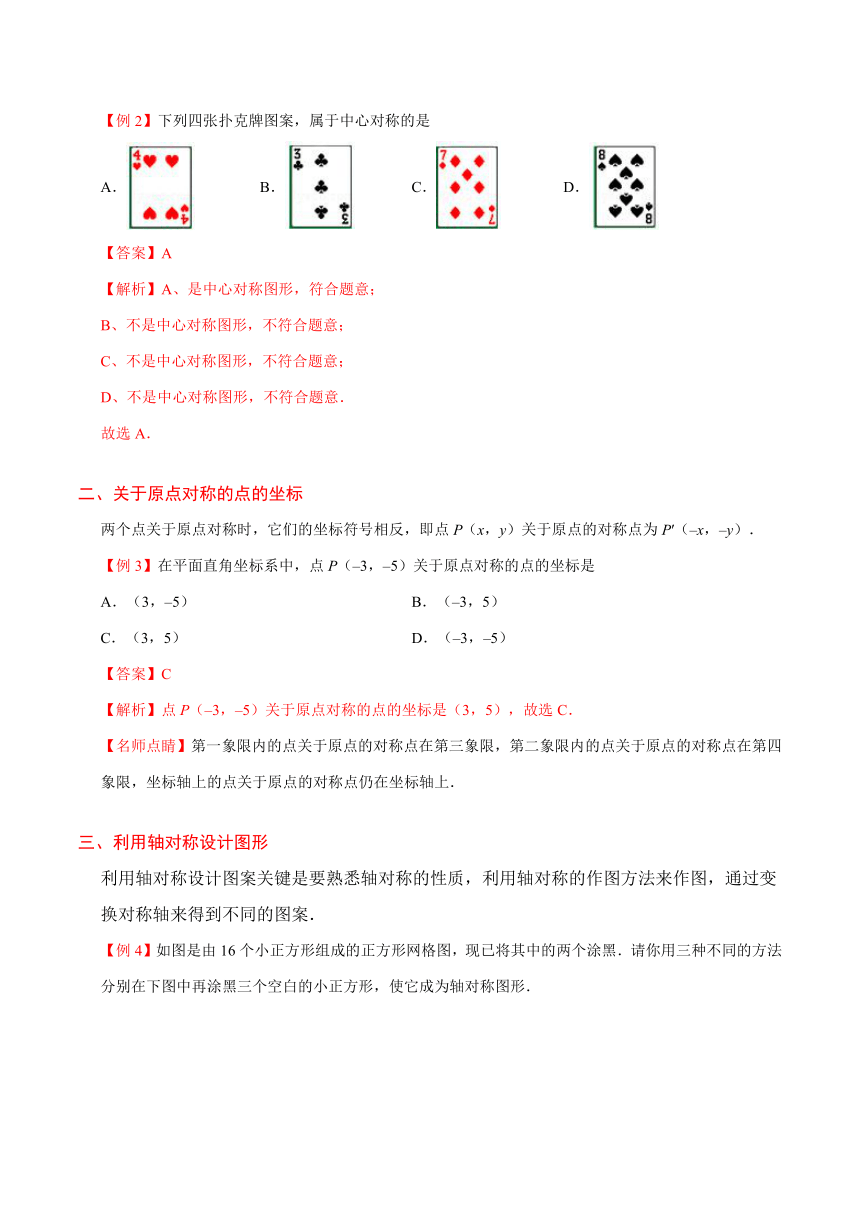
【例2】下列四张扑克牌图案,属于中心对称的是
A. B. C. D.
【答案】A
【解析】A、是中心对称图形,符合题意; B、不是中心对称图形,不符合题意; C、不是中心对称图形,不符合题意; D、不是中心对称图形,不符合题意. 故选A.
二、关于原点对称的点的坐标
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(–x,–y).
【例3】在平面直角坐标系中,点P(–3,–5)关于原点对称的点的坐标是
A.(3,–5) B.(–3,5)
C.(3,5) D.(–3,–5)
【答案】C
【解析】点P(–3,–5)关于原点对称的点的坐标是(3,5),故选C.
【名师点睛】第一象限内的点关于原点的对称点在第三象限,第二象限内的点关于原点的对称点在第四象限,坐标轴上的点关于原点的对称点仍在坐标轴上.
三、利用轴对称设计图形
利用轴对称设计图案关键是要熟悉轴对称的性质,利用轴对称的作图方法来作图,通过变换对称轴来得到不同的图案.
【例4】如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用三种不同的方法分别在下图中再涂黑三个空白的小正方形,使它成为轴对称图形.
【答案】见解析
【解析】如图所示
四、利用平移设计图形
确定一个基本图案按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案.通过改变平移的方向和距离可使图案变得丰富多彩.
【例5】如图,它是由哪个基本图形经过怎样的变化得到的?
【答案】见解析
【解析】是由基本图形向右平移,再向下平移,再向左平移,然后再由基本图形利用轴对称结合平移,得出.
四、利用旋转设计图形
【例6】(1)请写出是旋转对称图形的两种多边形(正三角形除外)的名称,并分别写出其旋转角α的最小值;
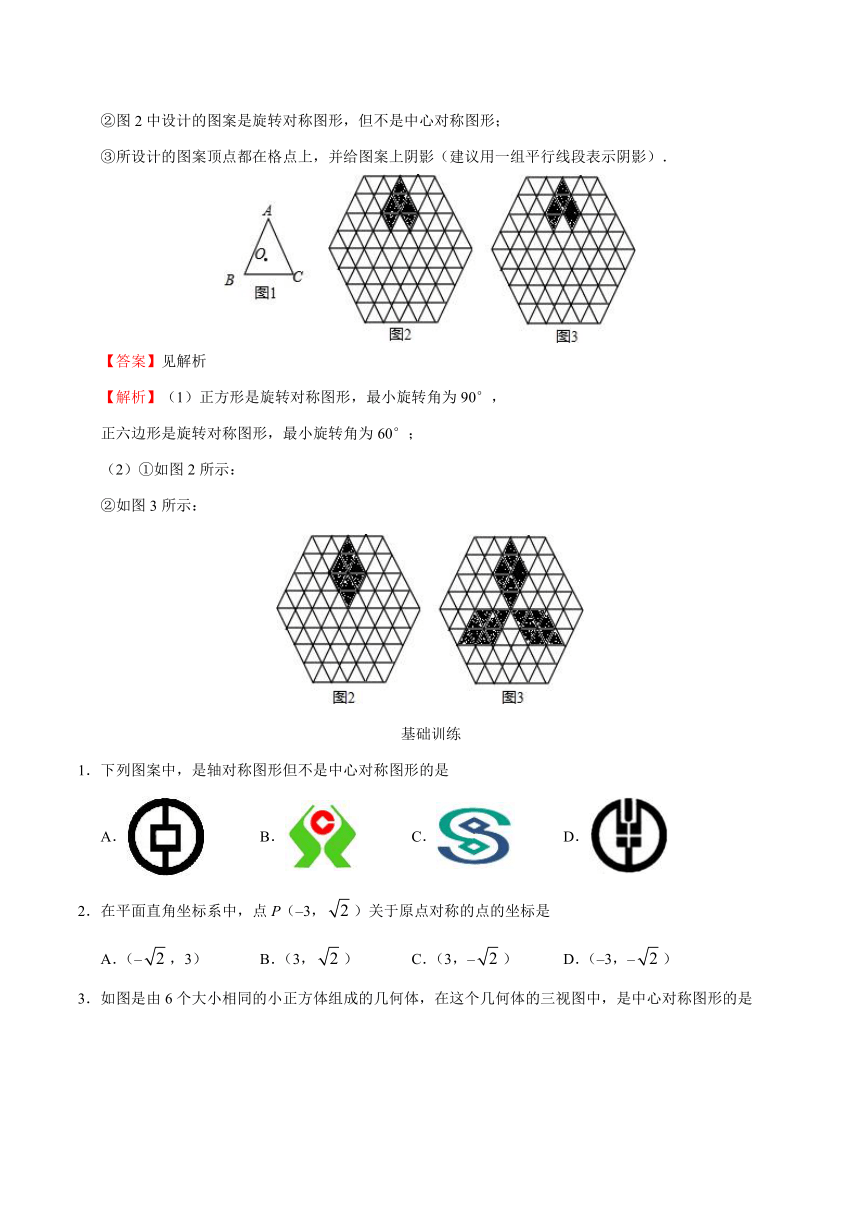
(2)下面的网格图都是由边长为1的正三角形组成的,请以图中给出的图案为基本图形(其顶点均在格点上),在图1、图2中再分别添加若干个基本图形,使添加的图形与原基本图形组成一个新图案,要求:
①图1中设计的图案既是旋转对称图形又是轴对称图形;
②图2中设计的图案是旋转对称图形,但不是中心对称图形;
③所设计的图案顶点都在格点上,并给图案上阴影(建议用一组平行线段表示阴影).
【答案】见解析
【解析】(1)正方形是旋转对称图形,最小旋转角为90°,
正六边形是旋转对称图形,最小旋转角为60°;
(2)①如图2所示:
②如图3所示:
基础训练
1.下列图案中,是轴对称图形但不是中心对称图形的是
A. B. C. D.
2.在平面直角坐标系中,点P(–3,)关于原点对称的点的坐标是
A.(–,3) B.(3,) C.(3,–) D.(–3,–)
3.如图是由6个大小相同的小正方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是
A.主视图 B.左视图 C.俯视图 D.主视图和左视图
4.下列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中看作由“基本图案”经过平移得到的是
A. B.
C. D.
5.将点A绕另一个点O旋转一周,点A在旋转过程中所经过的路线是__________.
6.在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距__________cm.
7.如图,在平面直角坐标系中,图形①,②关于点P中心对称.
(1)画出对称中心P,并写出点P的坐标;
(2)将图形②向下平移4个单位长度,画出平移后的图形③,并判断图形③与图形①的位置关系.(直接写出结果)
8.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(–3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,–4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转180°可以得到△A2B2C2,请直接写出旋转中心的坐标.
9.△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(–2,3),点B的坐标为(–1,1),点C的坐标为(0,2).
(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位长度,作出平移后的△A2B2C2.
(3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为(__________,__________).
能力测试
10.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为
A.(–4,–5) B.(–5,–4)
C.(–3,–4) D.(–4,–3)
11.已知点A(x–2,3)与点B(x+4,y–5)关于原点对称,则yx的值是
A. 2 B. C. 4 D. 8
12.将线段AB绕点O顺时针旋转180°得到线段A′B′,那么A(–3,2)的对应点A′的坐标是__________.
13.以等腰直角△ABC的斜边AB所在的直线为对称轴,作这个△ABC的对称图形△,则所得到的四边形ACBC′一定是__________.
14.如图,方格纸上画有AB、CD两条线段,按下列要求作图(保留作图痕迹,不要求写出作法).
(1)请你在图①中画出线段AB、CD关于点E成中心对称的图形;
(2)请你在图②中画出线段AB关于CD所在直线成轴对称的图形;
(3)请你在图③中添上一条线段,使图中3条线段组成一个轴对称图形,请画出所有情形.
真题练习
15.(2019·张家界)下列图形中,既是中心对称图形,又是轴对称图形的是
A. B.
C. D.
16.(2019·成都)在平面直角坐标系中,点P(–3,–5)关于原点对称的点的坐标是
A.(3,–5) B.(–3,5)
C.(3,5) D.(–3,–5)
17.(2019·烟台)在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是
A. B.
C. D.
18.(2019·攀枝花)下列平面图形中,既是中心对称图形,又是轴对称图形的是
A.菱形 B.等边三角形
C.平行四边形 D.等腰梯形
19.(2019?台州)在下列四个新能源汽车车标的设计图中,属于中心对称图形的是
A. B.
C. D.
20.(2019?江西)小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有
A.3个 B.4个 C.5个 D.无数个
21.(2019?大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab=__________.
22.(2019?温州)如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
(1)画出一个面积最小的PAQB.
(2)画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
参考答案
1.【答案】D
2.【答案】C
【解析】点P(–3,)关于原点对称的点的坐标是(3,–),故选C.
3.【答案】C
【解析】观察几何体,可得三视图如图所示:
可知俯视图是中心对称图形,故选C.
4.【答案】B
【解析】观察图形可知,图案B可以看作由“基本图案”经过平移得到.故选B.
5.【答案】圆
【解析】依题意,点A绕点O旋转一周的路线是圆.
6.【答案】2
【解析】根据中心对称的性质得,OB=OB′,OC=1,又BC=2,
由勾股定理得BO=,所以BB′=2OB=.
故答案为.
7.【解析】(1)画点P,P(1,5);
(2)画图形③,图形③与图形①关于点Q(1,3)成中心对称.
10.【答案】A
11.【答案】B
【解析】∵点A(x–2,3)与点B(x+4,y–5)关于原点对称,
∴,解得:,
则yx=2–1=. 故选B.
12.【答案】(3,–2)
【解析】∵将线段AB绕点O顺时针旋转180°得到线段A′B′,
∴线段AB与线段A′B′的对应点关于原点对称,
∵点A坐标为(–3,2),
∴点A的对应点A′的坐标是(3,–2);
故答案为:(3,–2).
13.【答案】正方形
14.【解析】(1)如图①所示:
(2)如图②所示:
(3)共4种画法,如图③所示.
第一种:以线段CD的垂直平分线为对称轴;
第二种:以线段CD所在的直线为对称轴;
第三种:以线段AB所在的直线为对称轴;
第四种:以线段AB的垂直平分线为对称轴.
15.【答案】C
16.【答案】C
【解析】点P(–3,–5)关于原点对称的点的坐标是(3,5),故选C.
17.【答案】C
【解析】A、是轴对称图形,不是中心对称图形,故此选项错误;
B、是轴对称图形,也是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项正确;
D、是轴对称图形,也是中心对称图形,故此选项错误.
故选C.
18.【答案】A
【解析】A、菱形既是中心对称图形,也是轴对称图形,故本选项正确;
B、等边三角形不是中心对称图形,是轴对称图形,故本选项错误;
C、平行四边形是中心对称图形,不是轴对称图形,故本选项错误;
D、等腰梯形不是中心对称图形,是轴对称图形,故本选项错误.
故选A.
19.【答案】D
【解析】A、不是中心对称图形,本选项错误;
B、不是中心对称图形,本选项错误;
C、不是中心对称图形,本选项错误;
D、是中心对称图形,本选项正确.
故选D.
20.【答案】C
21.【答案】12
【解析】∵点A的坐标为(a,3),点B的坐标是(4,b),点A与点B关于原点O对称,
∴a=–4,b=–3,则ab=12.故答案为:12.
22.【解析】(1)答案不唯一,如图①所示:
(2)答案不唯一,如图②所示:
同课章节目录
