人教版数学初中九年级下册知识讲解,巩固练习(教学资料,补习资料):专题26.2 实际问题与反比例函数(含答案)
文档属性
| 名称 | 人教版数学初中九年级下册知识讲解,巩固练习(教学资料,补习资料):专题26.2 实际问题与反比例函数(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 548.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-30 00:00:00 | ||
图片预览




文档简介
知识
实际问题与反比例函数
1.一般地,建立反比例函数模型有以下两种常用方法:
(1)待定系数法
若题目提供的信息中明确此函数为反比例函数,则可设反比例函数解析式为,然后求出k的值即可.
(2)列方程法
若题目信息中变量之间的函数关系不明确,在这种情况下,通常是列出关于函数(y)和自变量(x)的方程,进而解出函数,得到函数解析式.
2.用反比例函数解决实际问题的步骤:
(1)审——审清题意,找出题目中的常量、变量,并审理清常量与变量之间的关系;
(2)设——根据常量与变量之间的关系,设出函数解析式,待定的系数用字母表示;
(3)列——由题目中的已知条件列出方程,求出待定系数;
(4)写——写出函数解析式,并注意解析式中变量的取值范围;
(5)解——用函数解析式去解决实际问题.
重点
重点
利用反比例函数知识解决实际问题
难点
反比例函数与其他学科的综合问题
易错
忽略实际问题中自变量的取值范围
一、几何问题与反比例函数
当问题中设计几何问题时,可根据其图形建模,构造反比例函数解析式,并运用其性质解决问题,但要注意自变量的取值范围.
【例1】如果矩形的面积为,那么它的长与宽之间的函数关系用图象表示大致是
A. B. C. D.
【答案】C
【解析】由矩形的面积公式可得xy=6,∴y=(x>0,y>0).图象在第一象限.故选C.
二、跨学科问题与反比例函数
跨学科问题中常见的反比例关系:
1.压力一定时,压强与受力面积成反比例.
2.当功率一定时,力与速度成反比例.
3.当电压一定时,用电器的输出功率与电阻成反比例.
4.当电压一定时,电流强度与电阻成反比例.
【例2】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内气压大于120 kPa时,气球将爆炸,为了安全起见,气球内的体积应
A.小于1.25 m3 B.大于1.25 m3 C.不小于0.8 m3 D.大于0.8 m
【答案】C
基础训练
1.购买斤水果需元,购买一斤水果的单价与的关系式是
A.y=(x>0) B.y=(x为自然数)
C.y=(x为整数) D.y=(x为正整数)
2.物体所受的压力F(N)与所受的压强P(Pa)及受力面积S(m2)满足关系式为P×S=F(S≠0),当压力F(N)一定时,P与S的图象大致是
A. B.
C. D.
3.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为
A.y= B.y=
C.y= D.y=
4.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A. B.
C. D.
5.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是
A. B.
C. D.
6.某产品的进价为元,该产品的日销量(件)是日销价(元)的反比例函数,且当售价为每件元时,每日可售出件,为获得日利润为元,售价应定为__________.
7.近视眼镜的度数(度)与镜片焦距(米)呈反比例,其函数关系式为.如果近似眼镜镜片的焦距米,那么近视眼镜的度数y为__________.
8.饮水机接通电源就进入自动程序,若在水温为时,接通电源后,水温和时间的关系如图.开机加热时每分钟上升,加热到,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至,饮水机自动开机,重复上述自动程序.若上午开机,则时能否喝到超过的水?说明理由.
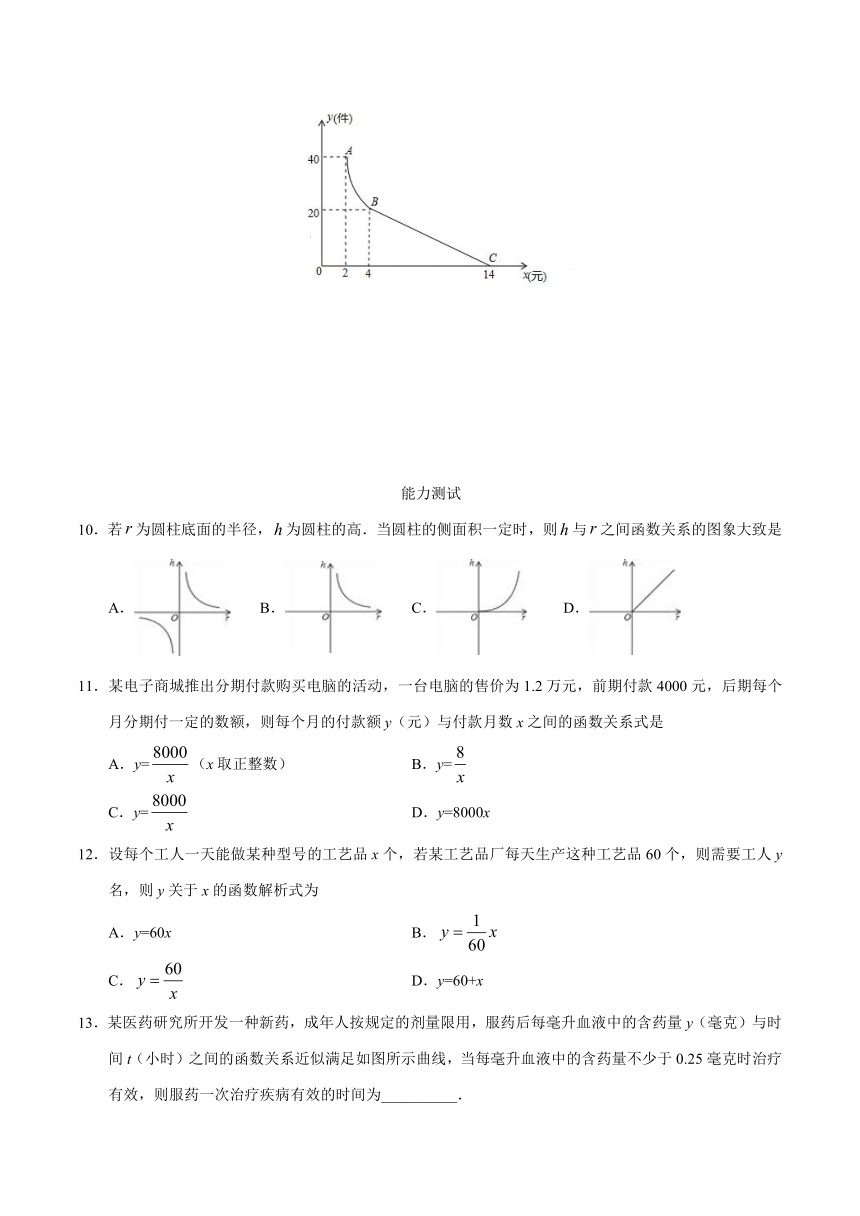
9.小成利用暑期参加社会实践,在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小成所有玩具的进价均2元/个,在销售过程中发现:每天玩具销售量y件与销售价格x元/件的关系如图所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小成销售这种玩具的日利润为w元.
(1)根据图象,求出y与x之间的函数关系式;
(2)若小成某天将价格定为超过4元(x>4),且销售利润为54元,求该天玩具的销售价格.
能力测试
10.若为圆柱底面的半径,为圆柱的高.当圆柱的侧面积一定时,则与之间函数关系的图象大致是
A. B. C. D.
11.某电子商城推出分期付款购买电脑的活动,一台电脑的售价为1.2万元,前期付款4000元,后期每个月分期付一定的数额,则每个月的付款额y(元)与付款月数x之间的函数关系式是
A.y=(x取正整数) B.y=
C.y= D.y=8000x
12.设每个工人一天能做某种型号的工艺品x个,若某工艺品厂每天生产这种工艺品60个,则需要工人y名,则y关于x的函数解析式为
A.y=60x B.
C. D.y=60+x
13.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为__________.
14.一辆汽车匀速通过某段公路,所需时间与行驶速度满足函数关系:,其图象为如图所示的一段曲线且端点为和.
(1)求k和m的值;
(2)若行驶速度不得超过,则汽车通过该路段最少需要多少时间?
真题练习
15.(2019·四川乐山)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(°C)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10 °C,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
参考答案
4.【答案】D
【解析】由表格中的已知数据可得:100×60=80×75-60×100=40×150=20×300=6000,∴xy=6000,
∴y与x间的函数关系式为:.故选D.
5.【答案】C
【解析】由题意可得:y=.故选C.
6.【答案】元
【解析】设y与x的函数解析式为y=(k≠0).由题意得40=,解得k=4000,
所以y=.设为获得日利润1500元,售价应定为x元,根据题意得y(x?50)=1500,
即(x?50)=1500,解得x=80.经检验:x=80是原分式方程的解.
答:为获得日利润1500元,售价应定为80元.故答案为80元.
7.【答案】400
【解析】把代入,,故答案为:400.
将代入,解得,
∴,
令,解得.
所以,饮水机的一个循环周期为分钟.每一个循环周期内,在时间段内,水温超过.
∴开机,则时不能喝到超过的水.
9.【解析】(1)当时,设,
10.【答案】B
【解析】根据圆柱的侧面积公式h·2πr=S,∴,故选B.
11.【答案】A
【解析】由题意可知,后期分期付款总额为:12000-4000=8000(元),每个月的付款额为y(元),付款期数为x,∴(x为正整数).故选A.
12.【答案】C
【解析】∵每个工人一天能做某种型号的工艺品x个,若某工艺品厂每天生产这种工艺品60个,需要工人y名,∴,∴,故选C.
13.【答案】
【解析】由题意和图可知:线段和曲线都过点(1,4),
∴,
∴,
当时,有,解得:和,
∵,
∴服一次药的有效治疗时间为小时.故答案为:.
代入得,
解得,
∴AB解析式为:y=2x+10(0≤x<5).
∵B在线段AB上当x=5时,y=20,
∴B坐标为(5,20),
∴线段BC的解析式为:y=20(5≤x<10),
设双曲线CD解析式为:y=(k2≠0),
∵C(10,20),
∴k2=200,
