2019华师大版八年级上册数学课件13.3.1等腰三角形的性质课件(14张ppt)
文档属性
| 名称 | 2019华师大版八年级上册数学课件13.3.1等腰三角形的性质课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 00:00:00 | ||
图片预览






文档简介
课件14张PPT。教学课件
数学 八年级上册 华东师大版
第13章 全等三角形
13.3 等腰三角形一、复习
1、什么叫轴对称图形和轴对称? 答:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。这条直线叫做对称轴。 2、轴对称与轴对称图形的联系和区别是什么? 对于两个图形,如果沿一条直线对折后,它们能完全重合,那么称这两个图形成轴对称。这条直线就是对称轴。二、复习
1、角是轴对称图形吗?对称轴是什么?性质有哪些? 答:是,对称轴是角平分线所在的直线
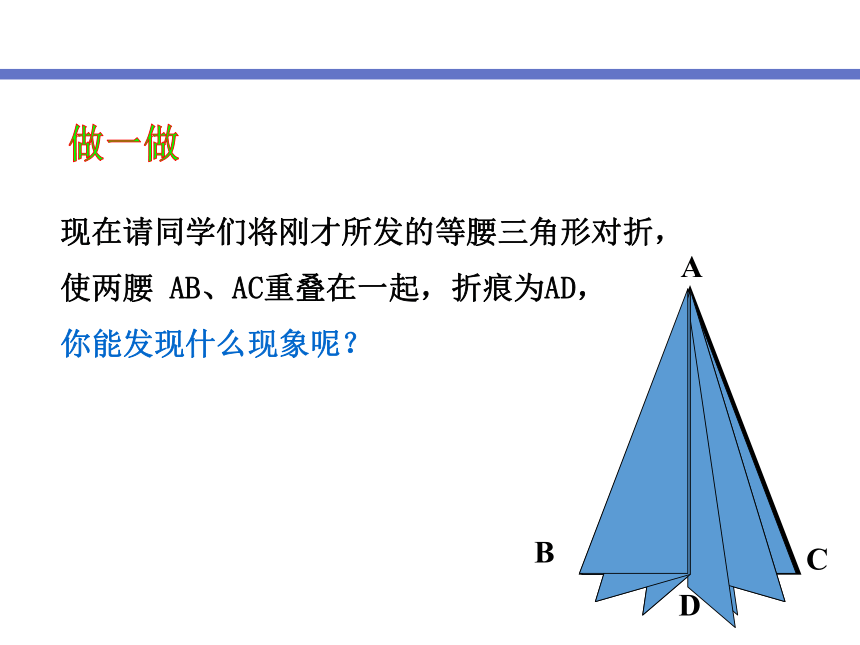
角平分线上的点到角两边的距离相等。 2、线段是轴对称图形吗?对称轴是什么?性质有哪些呢? 答:是,对称轴是它的垂直平分线,线段的垂直平分线到线段的两个端点的距离相等。做一做现在请同学们将刚才所发的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?不重合!“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高为什么不一样?1.等腰三角形是轴对称图形2.等腰三角形两个底角相等,简写成“等边对等角”3.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.简称“三线合一”等腰三角形的三个性质“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的“等边对等角”必须在同一个等腰三角形中才成立 例1 已知:在△ABC中,AB=AC,∠B=80。求∠C和∠A的度数.解:(已知)(等边对等角)(三角形内角和等于 )例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30。.求∠1和∠ADC的度数.解:∵ AB=AC,D是BC边上的中点∠ADC= 90°∵ ∠BAC=180°-30°-30°=120°(三线合一)小结本节课你学到了什么?2、等腰三角形的性质:(2)等腰三角形底边上的中线,底边上的高和顶角平分线互相重合(简称“三线合一”)(1)等腰三角形的两底角相等(简写“等边对等角”)与同伴交流你在探索思路的过程中的具体做法.下列各说法对吗?为什么?1、等腰三角形两底角的平分线相等.
2、等腰三角形两腰上的中线相等.
3、等腰三角形两腰上的高相等.思考一、等腰三角形性质定理:1、将命题“等边对等角”写成“如果…那么…”的形式,并写出它的题设与结论。如果一个三角形有两条边相等,那么这两条边所对的角也相等2、说出上述命题的逆命题,它是真命题还是假命题?如果一个三角形有两个角相等,那么这两个角所对的边相等简称为“等角对等边”
数学 八年级上册 华东师大版
第13章 全等三角形
13.3 等腰三角形一、复习
1、什么叫轴对称图形和轴对称? 答:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。这条直线叫做对称轴。 2、轴对称与轴对称图形的联系和区别是什么? 对于两个图形,如果沿一条直线对折后,它们能完全重合,那么称这两个图形成轴对称。这条直线就是对称轴。二、复习
1、角是轴对称图形吗?对称轴是什么?性质有哪些? 答:是,对称轴是角平分线所在的直线
角平分线上的点到角两边的距离相等。 2、线段是轴对称图形吗?对称轴是什么?性质有哪些呢? 答:是,对称轴是它的垂直平分线,线段的垂直平分线到线段的两个端点的距离相等。做一做现在请同学们将刚才所发的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?不重合!“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高为什么不一样?1.等腰三角形是轴对称图形2.等腰三角形两个底角相等,简写成“等边对等角”3.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.简称“三线合一”等腰三角形的三个性质“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的“等边对等角”必须在同一个等腰三角形中才成立 例1 已知:在△ABC中,AB=AC,∠B=80。求∠C和∠A的度数.解:(已知)(等边对等角)(三角形内角和等于 )例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30。.求∠1和∠ADC的度数.解:∵ AB=AC,D是BC边上的中点∠ADC= 90°∵ ∠BAC=180°-30°-30°=120°(三线合一)小结本节课你学到了什么?2、等腰三角形的性质:(2)等腰三角形底边上的中线,底边上的高和顶角平分线互相重合(简称“三线合一”)(1)等腰三角形的两底角相等(简写“等边对等角”)与同伴交流你在探索思路的过程中的具体做法.下列各说法对吗?为什么?1、等腰三角形两底角的平分线相等.
2、等腰三角形两腰上的中线相等.
3、等腰三角形两腰上的高相等.思考一、等腰三角形性质定理:1、将命题“等边对等角”写成“如果…那么…”的形式,并写出它的题设与结论。如果一个三角形有两条边相等,那么这两条边所对的角也相等2、说出上述命题的逆命题,它是真命题还是假命题?如果一个三角形有两个角相等,那么这两个角所对的边相等简称为“等角对等边”
