人教A版选修2-2 1.6微积分基本定理 23张
文档属性
| 名称 | 人教A版选修2-2 1.6微积分基本定理 23张 |

|
|
| 格式 | zip | ||
| 文件大小 | 798.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 16:03:26 | ||
图片预览







文档简介
课件23张PPT。微积分基本定理高中人教A版选修《数学2-2》复习:1、定积分是怎样定义?设函数f(x)在[a,b]上连续,在[a,b]中任意插入n-1个分点:把区间[a,b]等分成n个小区间,则,这个常数A称为f(x)在[a,b]上的定积分(简称积分)
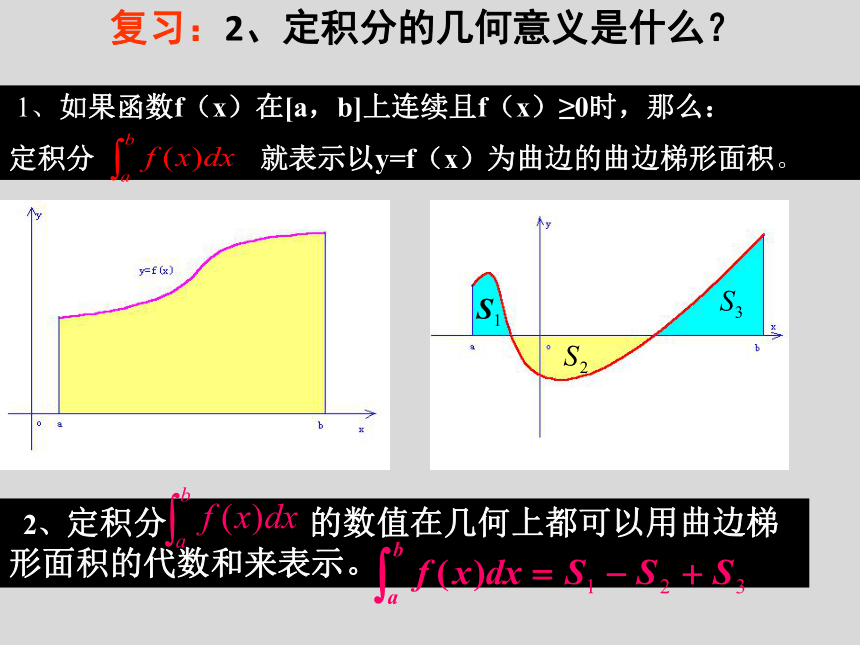
记作积分上限积分下限 1、如果函数f(x)在[a,b]上连续且f(x)≥0时,那么:
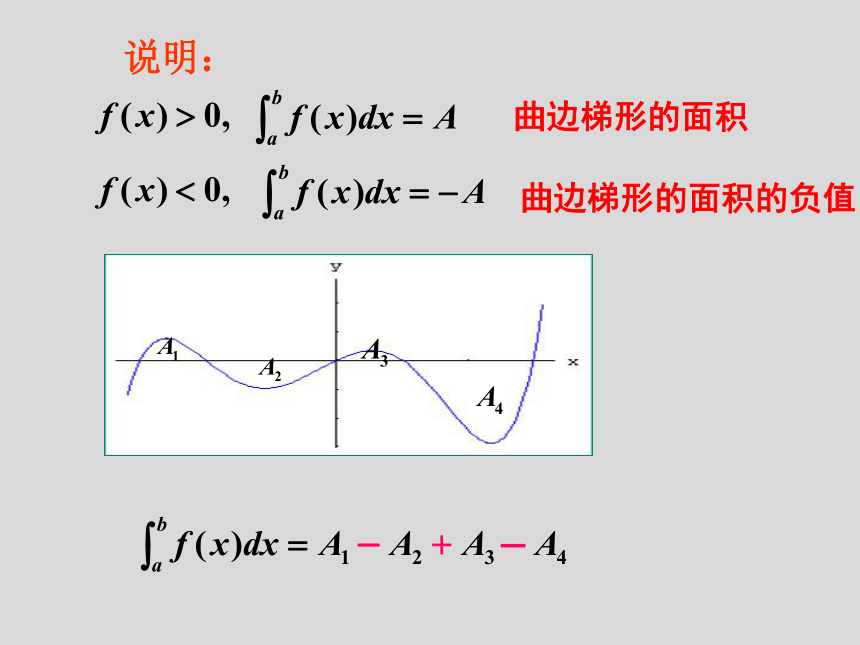
定积分 就表示以y=f(x)为曲边的曲边梯形面积。 2、定积分 的数值在几何上都可以用曲边梯形面积的代数和来表示。复习:2、定积分的几何意义是什么?曲边梯形的面积曲边梯形的面积的负值说明:定积分的简单性质题型1:定积分的简单性质的应用点评:运用定积分的性质可以化简定积分计算,也可以把一个函数的定积分化成几个简单函数定积分的和或差题型2:定积分的几何意义的应用8问题1:你能求出下列格式的值吗?不妨试试。问题2:一个作变速直线运动的物体的运动规律S=S(t)。由导数的概念可以知道,它在任意时刻t的速度v(t)=S’(t)。设这个物体在时间段〔a,b〕内的位移为S,你能分别用S(t),v(t)来表示S吗?从中你能发现导数和定积分的内在联系吗?另一方面,从导数角度来看:如果已知该变速直线运动的路程函数为s=s(t),则在时间区间[a,b]内物体的位移为s(b)–s(a), 所以又有 由于 ,即s(t)是v(t)的原函数,这就是说,定积分 等于被积函数v(t)的原函数s(t)在区间[a,b]上的增量s(b)–s(a). 从定积分角度来看:如果物体运动的速度函数为v=v(t),那么在时间区间[a,b]内物体的位移s可以用定积分表示为y(a)PDC探究点2 微积分基本定理y微积分基本定理:如果f(x)是区间[a,b]上的连续函数,并且F'(x)=f(x),那么这个结论叫做微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz formula).说明:
牛顿-莱布尼茨公式提供了计算定积分的简便的基本方法,即求定积分的值,只要求出被积函数 f(x)的一个原函数F(x),然后计算原函数在区间[a,b]上的增量F(b)–F(a)即可.该公式把计算定积分归结为求原函数的问题。回顾:基本初等函数的导数公式基本初等函数的原函数公式例1 计算下列定积分 解(1)练习1:我们发现:
定积分的值可取正值也可取负值,还可能是0;(1)当曲边梯形位于x轴上方时,定积分的值取正值;(2)当曲边梯形位于x轴下方时,定积分的值取负值;
(3)当曲边梯形位于x轴上方的面积等于位于x轴下方
的面积时,定积分的值为0.定积分公式1.微积分基本定理:2.基本初等函数的原函数公式归纳概括
记作积分上限积分下限 1、如果函数f(x)在[a,b]上连续且f(x)≥0时,那么:
定积分 就表示以y=f(x)为曲边的曲边梯形面积。 2、定积分 的数值在几何上都可以用曲边梯形面积的代数和来表示。复习:2、定积分的几何意义是什么?曲边梯形的面积曲边梯形的面积的负值说明:定积分的简单性质题型1:定积分的简单性质的应用点评:运用定积分的性质可以化简定积分计算,也可以把一个函数的定积分化成几个简单函数定积分的和或差题型2:定积分的几何意义的应用8问题1:你能求出下列格式的值吗?不妨试试。问题2:一个作变速直线运动的物体的运动规律S=S(t)。由导数的概念可以知道,它在任意时刻t的速度v(t)=S’(t)。设这个物体在时间段〔a,b〕内的位移为S,你能分别用S(t),v(t)来表示S吗?从中你能发现导数和定积分的内在联系吗?另一方面,从导数角度来看:如果已知该变速直线运动的路程函数为s=s(t),则在时间区间[a,b]内物体的位移为s(b)–s(a), 所以又有 由于 ,即s(t)是v(t)的原函数,这就是说,定积分 等于被积函数v(t)的原函数s(t)在区间[a,b]上的增量s(b)–s(a). 从定积分角度来看:如果物体运动的速度函数为v=v(t),那么在时间区间[a,b]内物体的位移s可以用定积分表示为y(a)PDC探究点2 微积分基本定理y微积分基本定理:如果f(x)是区间[a,b]上的连续函数,并且F'(x)=f(x),那么这个结论叫做微积分基本定理(fundamental theorem of calculus),又叫牛顿-莱布尼茨公式(Newton-Leibniz formula).说明:
牛顿-莱布尼茨公式提供了计算定积分的简便的基本方法,即求定积分的值,只要求出被积函数 f(x)的一个原函数F(x),然后计算原函数在区间[a,b]上的增量F(b)–F(a)即可.该公式把计算定积分归结为求原函数的问题。回顾:基本初等函数的导数公式基本初等函数的原函数公式例1 计算下列定积分 解(1)练习1:我们发现:
定积分的值可取正值也可取负值,还可能是0;(1)当曲边梯形位于x轴上方时,定积分的值取正值;(2)当曲边梯形位于x轴下方时,定积分的值取负值;
(3)当曲边梯形位于x轴上方的面积等于位于x轴下方
的面积时,定积分的值为0.定积分公式1.微积分基本定理:2.基本初等函数的原函数公式归纳概括
