人教数学九下26.1.2反比例函数的图象和性质课件(20张ppt)
文档属性
| 名称 | 人教数学九下26.1.2反比例函数的图象和性质课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 601.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-01 00:00:00 | ||
图片预览







文档简介
课件20张PPT。反比例函数的图象和性质学习目标:
通过观察、交流、探索,归纳出反比例
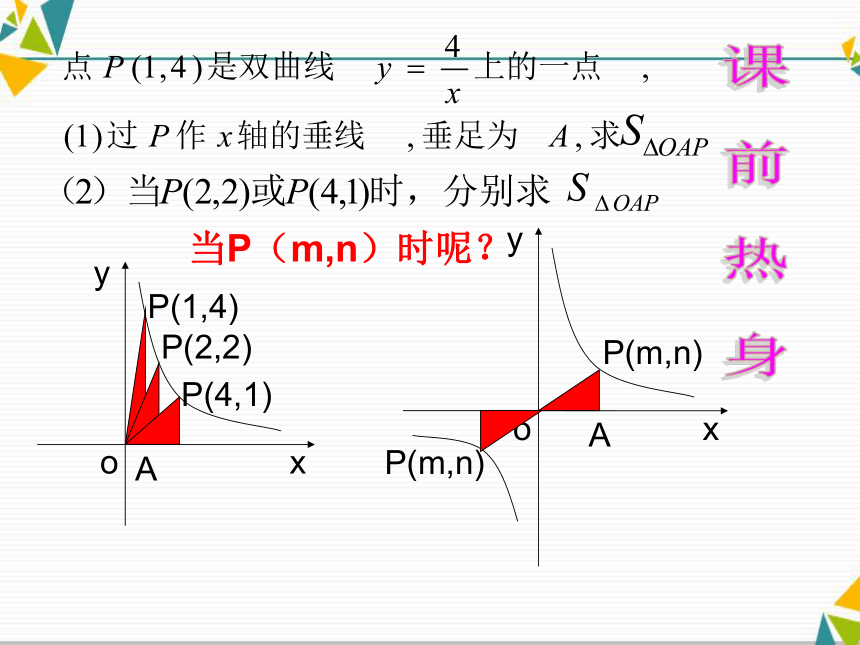
函数中图形的面积与系数k之间的关系,并会利用其关系灵活解题面 积 问 题当P(m,n)时呢?P(1,4)AoyP(2,2)P(4,1)课 前 热 身想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?再 接 再 厉1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为( )(m,n)基 础 演 练2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
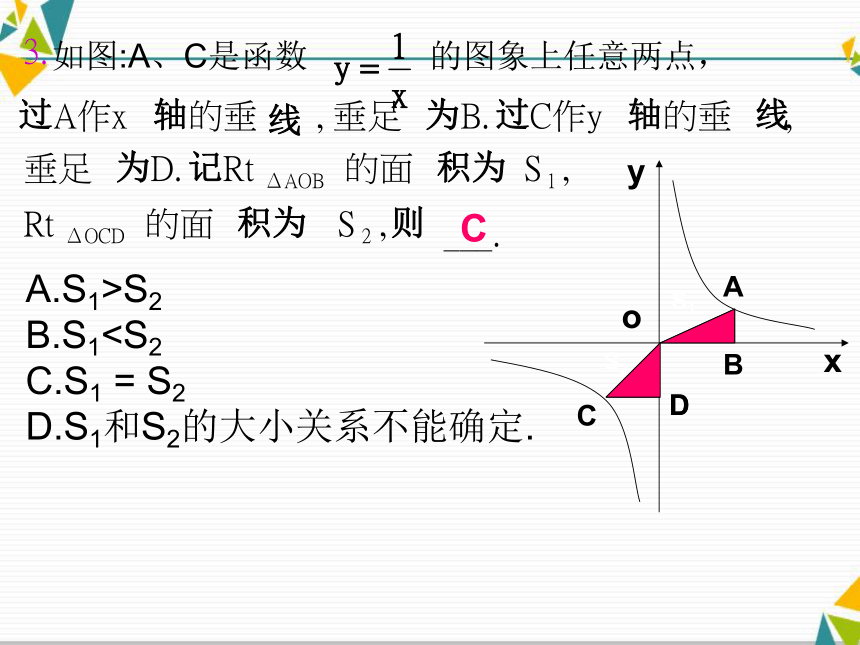
关系式是 .如图:A、C是函数 的图象上任意两点,A.S1>S2
B.S1C.S1 = S2
D.S1和S2的大小关系不能确定. C___.,S 的面Rt,S 的面RtD.垂足,的垂C作yB.垂足, 的垂A作x3.2ΔOCD1ΔAOB则积为积为记为线轴过为线轴过AA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S24、PAoyxQB举一反 三 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式训练一(A)s=1 (B) s=2
(C)1y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于 ( ) 变式训练二CA.S = 1 B.1C.S = 2 D.S>2oS1yxACyxB活 学 巧 练如图,在反比例函数的图象上,有点,它们的横坐标依次为1,2,3,4,求的值。P1,P2,P3,P4……小结与反思如图,已知反比例函数 的图象与一次函数
y= kx+4的图象相交于P、Q两点,且P点的纵坐标
是6,Q点的横坐标是-6
(1)求这个一次函数的解析式
(2)求三角形POQ的面积综 合 提 升
通过观察、交流、探索,归纳出反比例
函数中图形的面积与系数k之间的关系,并会利用其关系灵活解题面 积 问 题当P(m,n)时呢?P(1,4)AoyP(2,2)P(4,1)课 前 热 身想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?再 接 再 厉1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为( )(m,n)基 础 演 练2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .如图:A、C是函数 的图象上任意两点,A.S1>S2
B.S1
D.S1和S2的大小关系不能确定. C___.,S 的面Rt,S 的面RtD.垂足,的垂C作yB.垂足, 的垂A作x3.2ΔOCD1ΔAOB则积为积为记为线轴过为线轴过AA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S24、PAoyxQB举一反 三 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式训练一(A)s=1 (B) s=2
(C)1
y= kx+4的图象相交于P、Q两点,且P点的纵坐标
是6,Q点的横坐标是-6
(1)求这个一次函数的解析式
(2)求三角形POQ的面积综 合 提 升
