人教数学九下27.2.2 相似三角形的性质课件(30张ppt)
文档属性
| 名称 | 人教数学九下27.2.2 相似三角形的性质课件(30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 643.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 00:00:00 | ||
图片预览








文档简介
课件30张PPT。相似三角形的性质一、复习旧课 导入新课(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)你知道几种判定两个三角形相似的方法?(1)定义(三边对应成比例,三角对应相等)(2)相似三角形判定的预备定理:(3)三边对应成比例,两三角形相似(4)两边对应成比例且夹角相等,两三角形相似(5)两角对应相等,两三角形相似(6)两直角三角形的斜边和一条直角边对应成比例,
两直角三角形相似ABCA/B/C/①相似三角形的对应角_____________
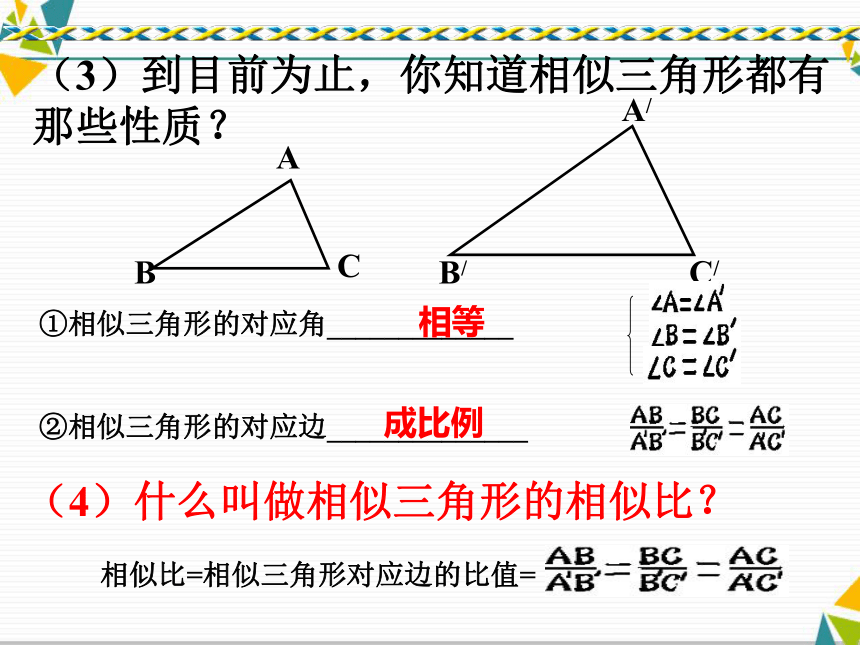
②相似三角形的对应边______________(4)什么叫做相似三角形的相似比?(3)到目前为止,你知道相似三角形都有那些性质?(5)一个三角形有三条重要线段:
________________
三角形的高线、中线、角平分线一、经历探索相似三角形性质的过程,并会运用
相似三角形的性质解决有关的问题。?
二、通过探索相似三角形性质的过程,渗透逻辑
推理方法,引导学生从直观发现向自觉说理
过渡。
三、采用类比方法、应用数形结合的数学思想,
培养学生从特殊到一般的认识规律,拓展学
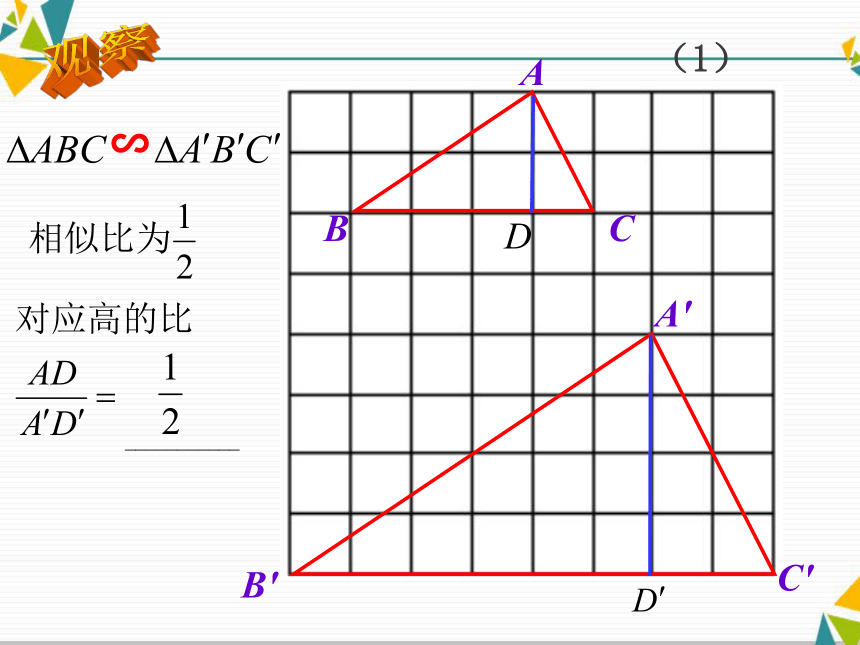
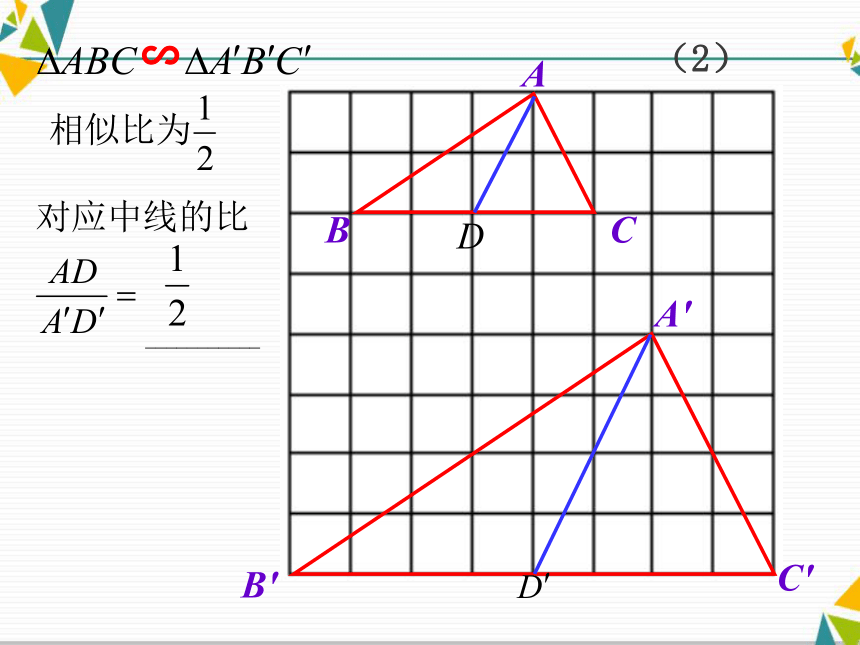
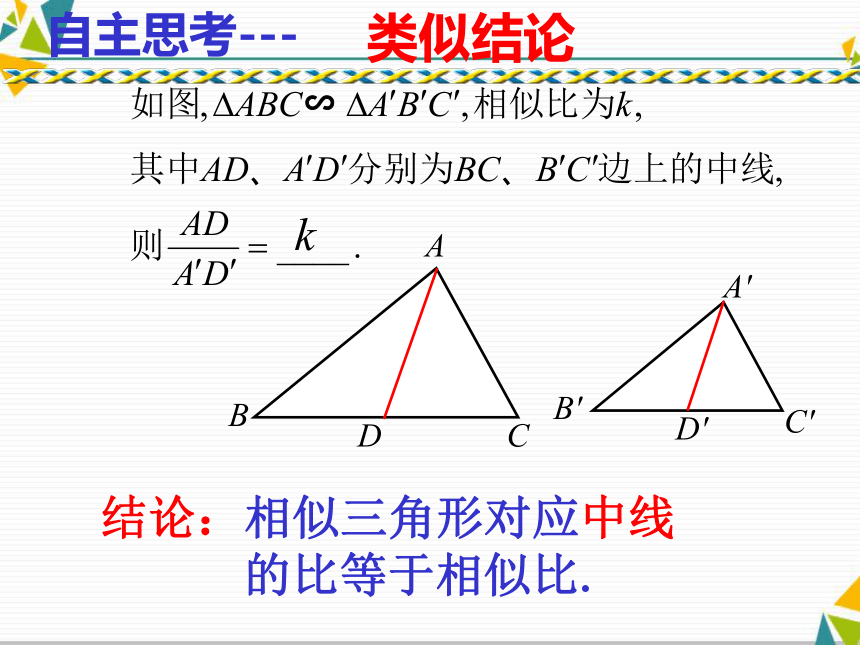
生思维,提高学生的创新意识和应用意识。学习目标(1)观察(2)(3)(二)合作交流探索新知两角对应相等,两三角形相似∽已知所以∠B=∠B( )相似三角形的对应角相等 ( ) 相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线
的比等于相似比.A′C′B′CBAE′E类似结论自主思考---结论:相似三角形对应角平
分线的比等于相似比.对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质练习一1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 3 2.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.25问题2:
两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(1)与(3)的相似比=______,
(1)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)1∶ 31∶ 21∶ 3如果△ABC∽△A’B’C’,相似比为k归纳: 相似三角形周长的比等于相似比。BACA’B’C’证明:因为 △ABC∽△A’B’C’ 所以对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质问题3:两个相似三角形的面积
之间有什么关系呢?相似三角形的性质用心观察123 1∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比= ____,
(1)与(2)的面积比=______
(1)与(3)的相似比=______,
(1)与(3)的面积比=______1∶ 4 1∶ 31∶ 9相似三角形面积的比等于相似比的平方.证明 ∵ △ABC∽△A′B′C′, ,,证明对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
2.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、8cm23.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4, 三 应用新知 体验成功例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,则?CDF的面积_____.BFEDCA1 : 220 cm2挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN的边长为xcm。
∵PN∥BC,∴△APN∽ △ABC
∴ 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似三角形的性质相似多边形也有同样的结论作业(1)习题27.2第6、7题
(2)将“相似三角形的对应中线的比等于相似比”,“相似三角形对应角平分线的比”等于相似比的过程写在作业本上谢谢大家
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)你知道几种判定两个三角形相似的方法?(1)定义(三边对应成比例,三角对应相等)(2)相似三角形判定的预备定理:(3)三边对应成比例,两三角形相似(4)两边对应成比例且夹角相等,两三角形相似(5)两角对应相等,两三角形相似(6)两直角三角形的斜边和一条直角边对应成比例,
两直角三角形相似ABCA/B/C/①相似三角形的对应角_____________
②相似三角形的对应边______________(4)什么叫做相似三角形的相似比?(3)到目前为止,你知道相似三角形都有那些性质?(5)一个三角形有三条重要线段:
________________
三角形的高线、中线、角平分线一、经历探索相似三角形性质的过程,并会运用
相似三角形的性质解决有关的问题。?
二、通过探索相似三角形性质的过程,渗透逻辑
推理方法,引导学生从直观发现向自觉说理
过渡。
三、采用类比方法、应用数形结合的数学思想,
培养学生从特殊到一般的认识规律,拓展学
生思维,提高学生的创新意识和应用意识。学习目标(1)观察(2)(3)(二)合作交流探索新知两角对应相等,两三角形相似∽已知所以∠B=∠B( )相似三角形的对应角相等 ( ) 相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线
的比等于相似比.A′C′B′CBAE′E类似结论自主思考---结论:相似三角形对应角平
分线的比等于相似比.对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质练习一1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 3 2.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.25问题2:
两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(1)与(3)的相似比=______,
(1)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)1∶ 31∶ 21∶ 3如果△ABC∽△A’B’C’,相似比为k归纳: 相似三角形周长的比等于相似比。BACA’B’C’证明:因为 △ABC∽△A’B’C’ 所以对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质问题3:两个相似三角形的面积
之间有什么关系呢?相似三角形的性质用心观察123 1∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比= ____,
(1)与(2)的面积比=______
(1)与(3)的相似比=______,
(1)与(3)的面积比=______1∶ 4 1∶ 31∶ 9相似三角形面积的比等于相似比的平方.证明 ∵ △ABC∽△A′B′C′, ,,证明对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
2.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、8cm23.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4, 三 应用新知 体验成功例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,则?CDF的面积_____.BFEDCA1 : 220 cm2挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN的边长为xcm。
∵PN∥BC,∴△APN∽ △ABC
∴ 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似三角形的性质相似多边形也有同样的结论作业(1)习题27.2第6、7题
(2)将“相似三角形的对应中线的比等于相似比”,“相似三角形对应角平分线的比”等于相似比的过程写在作业本上谢谢大家
