人教数学九下 28.1 锐角三角函数(1)课件(15张ppt)
文档属性
| 名称 | 人教数学九下 28.1 锐角三角函数(1)课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 00:00:00 | ||
图片预览



文档简介
课件15张PPT。九年级数学(下册)第二十八章
§28.1 锐角三角函数用数学视觉观察世界
用数学思维思考世界直角三角形
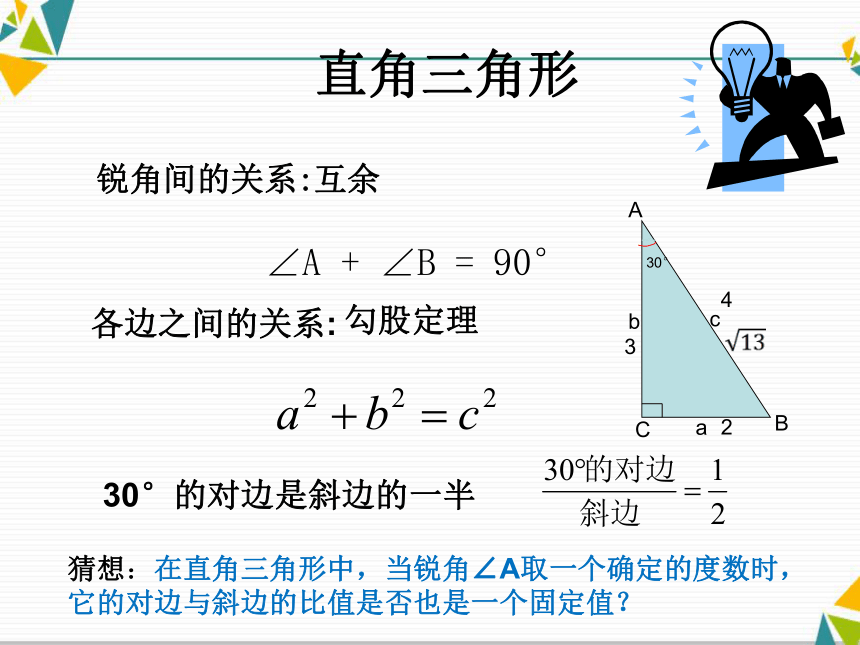
各边之间的关系:
ACBcab∠A + ∠B = 90°互余勾股定理锐角间的关系:2330°的对边是斜边的一半4猜想:在直角三角形中,当锐角∠A取一个确定的度数时,
它的对边与斜边的比值是否也是一个固定值?30°规律:在直角三角形中,当锐角∠A的度数一定时,无论这个直角三角形的大小如何,∠A的对边与斜边的比都是一个固定值. 猜想:在直角三角形中,当锐角∠A取一个确定的度数时,
它的对边与斜边的比值是否也是一个固定值?活动:每小组根据要求用几何画板作图,测量及计算:
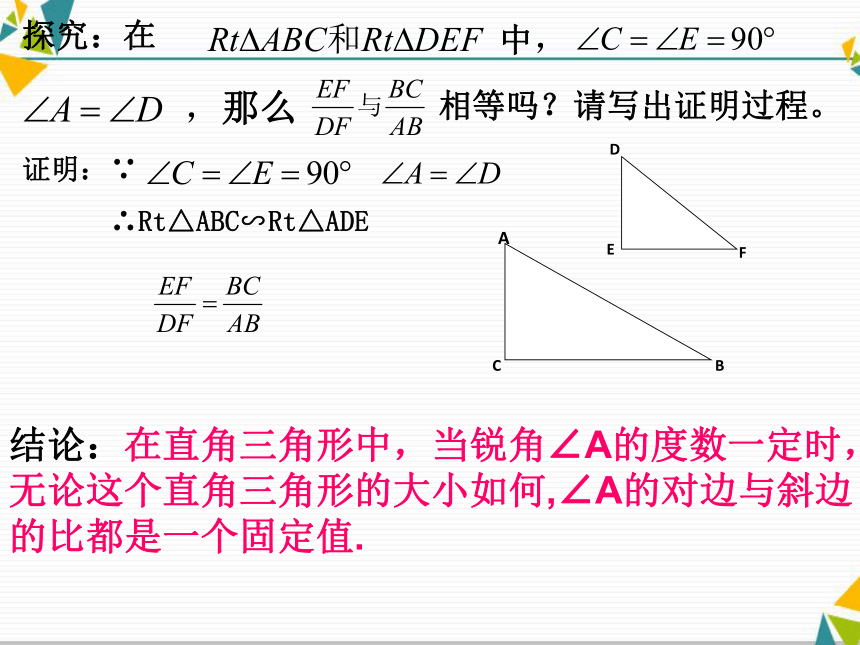
第一、二、三、四、五、六小组分别对应作出一个含有23°,37°,45°,50°,60°,75°的直角三角形,测量出所画角度的对边与斜边的长度,并求出它们的比值.结论:在直角三角形中,当锐角∠A的度数一定时,
无论这个直角三角形的大小如何,∠A的对边与斜边
的比都是一个固定值. ∵
∴Rt△ABC∽Rt△ADE
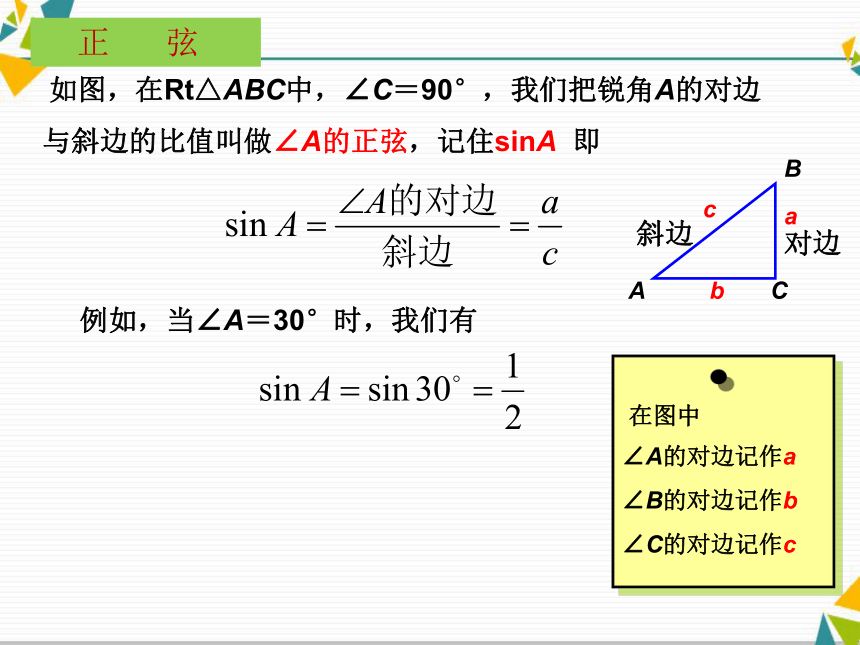
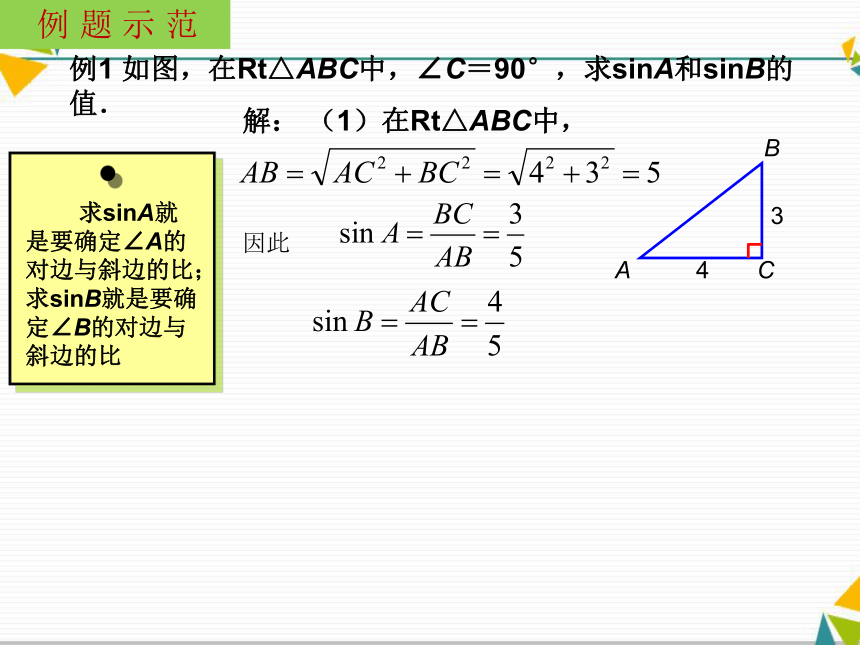
证明: 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记住sinA 即例如,当∠A=30°时,我们有对边 正 弦例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中,因此ABC34 例 题 示 范根据下图,求sinA和sinB的值.ABC35 练习解: (1)在Rt△ABC中,因此 随堂练习1.如图,在直角△ABC中,∠C=90o,若AB=5,AC=4,则A. B. C. D.=( )2.如图,已知点P的坐标是,则等于( )A. B. C. 3、将Rt△ABC的各边都扩大4倍,则锐角A的正弦值( )
A.不变 B.扩大4倍 C.原来的0.25 D.不能确定ADA例、在正方形网格中,△ABC的位置如图所示,则的值为( )A. B. C. D. B4、△ABC中,AB=AC=3,BC=2,则sinB= 。5、如图在Rt△ABC中, ∠ACB=90°,CD⊥AB,D为垂足,
若AC=4,BC=3,则sin∠ACD的值为( )。A. B. C. D.C6、在Rt△ABC中,∠C=90°,若AB=2AC,则=( )A. B. C. D.B7、如图,直角三角形ABC的面积为24cm2,直角边AB为6cm
,∠A是锐角,则 = ;8.如图所示,四边形ABCD中,∠B=90°,AB=2,
CD=8,AC⊥CD,若
则9.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,
则sinB的值为( )A. B. C. D.D10、在△ABC中,∠C=90°,BC=2, =
则边AC的长是( )A. B. C. D.11、在△ABC中,∠C=90°,sinA = ,则
BC:AC:AB=( )A.1:2:3 B.1: :3 C.2: :3 D.2: :DC
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距
离AC=3米,sin∠ABC=,则梯子长AB = 米。413.⊙O的半径为R,若圆心角∠AOB=a,则弦AB的长
为( )A. B.2Rsin a ? C. D.Rsina??A小结1、在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比值都是一个固定值.2、3、正弦必须在直角三角形中使用,如果没有,可根据题意适
当地构造直角三角形。
用数学思维思考世界直角三角形
各边之间的关系:
ACBcab∠A + ∠B = 90°互余勾股定理锐角间的关系:2330°的对边是斜边的一半4猜想:在直角三角形中,当锐角∠A取一个确定的度数时,
它的对边与斜边的比值是否也是一个固定值?30°规律:在直角三角形中,当锐角∠A的度数一定时,无论这个直角三角形的大小如何,∠A的对边与斜边的比都是一个固定值. 猜想:在直角三角形中,当锐角∠A取一个确定的度数时,
它的对边与斜边的比值是否也是一个固定值?活动:每小组根据要求用几何画板作图,测量及计算:
第一、二、三、四、五、六小组分别对应作出一个含有23°,37°,45°,50°,60°,75°的直角三角形,测量出所画角度的对边与斜边的长度,并求出它们的比值.结论:在直角三角形中,当锐角∠A的度数一定时,
无论这个直角三角形的大小如何,∠A的对边与斜边
的比都是一个固定值. ∵
∴Rt△ABC∽Rt△ADE
证明: 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记住sinA 即例如,当∠A=30°时,我们有对边 正 弦例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中,因此ABC34 例 题 示 范根据下图,求sinA和sinB的值.ABC35 练习解: (1)在Rt△ABC中,因此 随堂练习1.如图,在直角△ABC中,∠C=90o,若AB=5,AC=4,则A. B. C. D.=( )2.如图,已知点P的坐标是,则等于( )A. B. C. 3、将Rt△ABC的各边都扩大4倍,则锐角A的正弦值( )
A.不变 B.扩大4倍 C.原来的0.25 D.不能确定ADA例、在正方形网格中,△ABC的位置如图所示,则的值为( )A. B. C. D. B4、△ABC中,AB=AC=3,BC=2,则sinB= 。5、如图在Rt△ABC中, ∠ACB=90°,CD⊥AB,D为垂足,
若AC=4,BC=3,则sin∠ACD的值为( )。A. B. C. D.C6、在Rt△ABC中,∠C=90°,若AB=2AC,则=( )A. B. C. D.B7、如图,直角三角形ABC的面积为24cm2,直角边AB为6cm
,∠A是锐角,则 = ;8.如图所示,四边形ABCD中,∠B=90°,AB=2,
CD=8,AC⊥CD,若
则9.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,
则sinB的值为( )A. B. C. D.D10、在△ABC中,∠C=90°,BC=2, =
则边AC的长是( )A. B. C. D.11、在△ABC中,∠C=90°,sinA = ,则
BC:AC:AB=( )A.1:2:3 B.1: :3 C.2: :3 D.2: :DC
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距
离AC=3米,sin∠ABC=,则梯子长AB = 米。413.⊙O的半径为R,若圆心角∠AOB=a,则弦AB的长
为( )A. B.2Rsin a ? C. D.Rsina??A小结1、在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比值都是一个固定值.2、3、正弦必须在直角三角形中使用,如果没有,可根据题意适
当地构造直角三角形。
