13.2.1 画轴对称图形学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 13.2.1 画轴对称图形学案(要点讲解+当堂检测+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-02 10:26:04 | ||
图片预览

文档简介
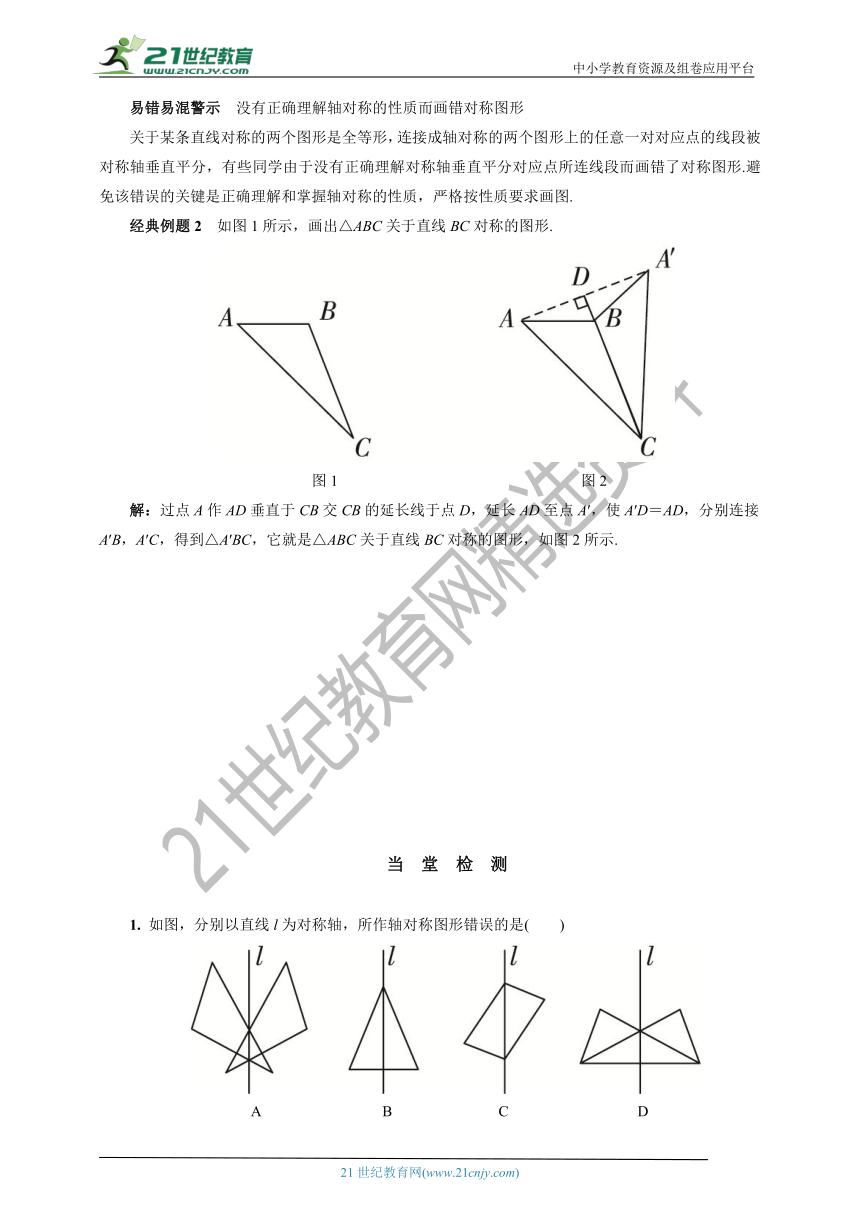
人教版数学八年级上册同步学案
第十三章 轴对称
13.2 画轴对称图形
13.2.1 画轴对称图形
要 点 讲 解
要点 画轴对称图形
1. 关于某直线成轴对称的两个图形之间的关系.
(1)由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同.
(2)新图形上的每一点都是原图形上的某一点关于直线l的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
2. 画轴对称图形的方法
由直线、线段或射线组成的图形,作出图形中一些特殊点(能确定图形的点)的对称点,连接这些对称点,就能得到原图形的轴对称图形.
画轴对称图形的方法简单归纳如下:
(1)找——在原图形上找特殊点(如线段的端点、线与线的交点等);
(2)作——作各个特殊点关于已知直线的对称点;
(3)连——按原图对应连接各对称点.
经典例题1 如图1所示,AB,C′B′分别是以直线MN为对称轴的两个三角形的一边,试画出完整的△ABC和△A′B′C′.
图1 图2
解析:要画出完整的△ABC和△A′B′C′,关键是作出点A,C′关于直线MN的对称点.
解:如图2所示,分别作点A,C′关于直线MN的对称点A′,C,连接AC,BC,A′B′,A′C′,得到完整的△ABC和△A′B′C′.
易错易混警示 没有正确理解轴对称的性质而画错对称图形
关于某条直线对称的两个图形是全等形,连接成轴对称的两个图形上的任意一对对应点的线段被对称轴垂直平分,有些同学由于没有正确理解对称轴垂直平分对应点所连线段而画错了对称图形.避免该错误的关键是正确理解和掌握轴对称的性质,严格按性质要求画图.
经典例题2 如图1所示,画出△ABC关于直线BC对称的图形.
图1 图2
解:过点A作AD垂直于CB交CB的延长线于点D,延长AD至点A′,使A′D=AD,分别连接A′B,A′C,得到△A′BC,它就是△ABC关于直线BC对称的图形,如图2所示.
当 堂 检 测
1. 如图,分别以直线l为对称轴,所作轴对称图形错误的是( )
A B C D
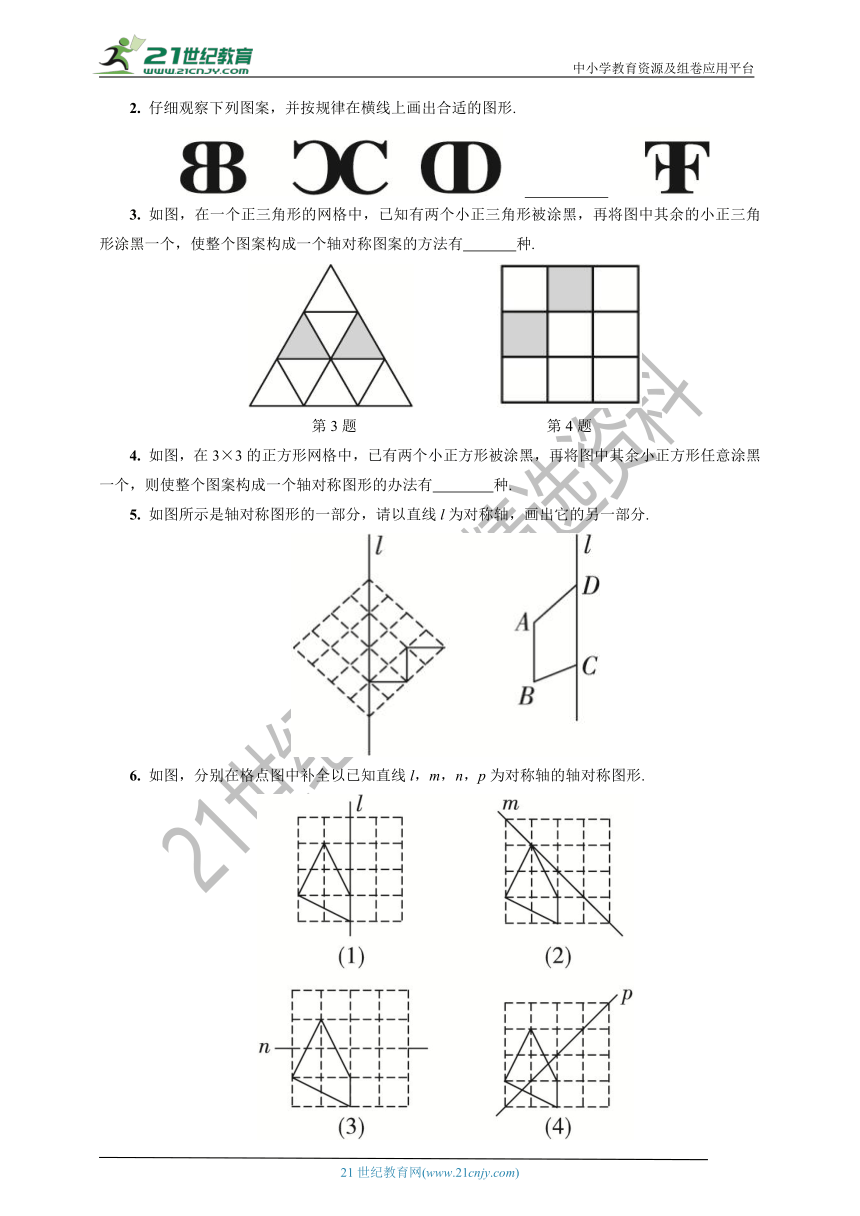
2. 仔细观察下列图案,并按规律在横线上画出合适的图形.
3. 如图,在一个正三角形的网格中,已知有两个小正三角形被涂黑,再将图中其余的小正三角形涂黑一个,使整个图案构成一个轴对称图案的方法有 种.
第3题 第4题
4. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,则使整个图案构成一个轴对称图形的办法有 种.
5. 如图所示是轴对称图形的一部分,请以直线l为对称轴,画出它的另一部分.
6. 如图,分别在格点图中补全以已知直线l,m,n,p为对称轴的轴对称图形.
7. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD的重叠部分的面积.
8. 如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.若AB长为15cm,求△PCD的周长.
当堂检测参考答案
1. C
2.
3. 3
4. 5
5. 解:如图所示.
6. 解:如图所示.
7. 解:(1)如图,△AEF即为所求. (2)S重叠部分=6.
8. 解:∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,∴AD=PD,CP=CB.∴△PCD的周长=PD+DC+CP=AD+DC+CB=AB=15cm.
第十三章 轴对称
13.2 画轴对称图形
13.2.1 画轴对称图形
要 点 讲 解
要点 画轴对称图形
1. 关于某直线成轴对称的两个图形之间的关系.
(1)由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同.
(2)新图形上的每一点都是原图形上的某一点关于直线l的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
2. 画轴对称图形的方法
由直线、线段或射线组成的图形,作出图形中一些特殊点(能确定图形的点)的对称点,连接这些对称点,就能得到原图形的轴对称图形.
画轴对称图形的方法简单归纳如下:
(1)找——在原图形上找特殊点(如线段的端点、线与线的交点等);
(2)作——作各个特殊点关于已知直线的对称点;
(3)连——按原图对应连接各对称点.
经典例题1 如图1所示,AB,C′B′分别是以直线MN为对称轴的两个三角形的一边,试画出完整的△ABC和△A′B′C′.
图1 图2
解析:要画出完整的△ABC和△A′B′C′,关键是作出点A,C′关于直线MN的对称点.
解:如图2所示,分别作点A,C′关于直线MN的对称点A′,C,连接AC,BC,A′B′,A′C′,得到完整的△ABC和△A′B′C′.
易错易混警示 没有正确理解轴对称的性质而画错对称图形
关于某条直线对称的两个图形是全等形,连接成轴对称的两个图形上的任意一对对应点的线段被对称轴垂直平分,有些同学由于没有正确理解对称轴垂直平分对应点所连线段而画错了对称图形.避免该错误的关键是正确理解和掌握轴对称的性质,严格按性质要求画图.
经典例题2 如图1所示,画出△ABC关于直线BC对称的图形.
图1 图2
解:过点A作AD垂直于CB交CB的延长线于点D,延长AD至点A′,使A′D=AD,分别连接A′B,A′C,得到△A′BC,它就是△ABC关于直线BC对称的图形,如图2所示.
当 堂 检 测
1. 如图,分别以直线l为对称轴,所作轴对称图形错误的是( )
A B C D
2. 仔细观察下列图案,并按规律在横线上画出合适的图形.
3. 如图,在一个正三角形的网格中,已知有两个小正三角形被涂黑,再将图中其余的小正三角形涂黑一个,使整个图案构成一个轴对称图案的方法有 种.
第3题 第4题
4. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,则使整个图案构成一个轴对称图形的办法有 种.
5. 如图所示是轴对称图形的一部分,请以直线l为对称轴,画出它的另一部分.
6. 如图,分别在格点图中补全以已知直线l,m,n,p为对称轴的轴对称图形.
7. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD的重叠部分的面积.
8. 如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.若AB长为15cm,求△PCD的周长.
当堂检测参考答案
1. C
2.
3. 3
4. 5
5. 解:如图所示.
6. 解:如图所示.
7. 解:(1)如图,△AEF即为所求. (2)S重叠部分=6.
8. 解:∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,∴AD=PD,CP=CB.∴△PCD的周长=PD+DC+CP=AD+DC+CB=AB=15cm.
