北师大版2019_2020学年九年级数学下册第三章圆检测卷含答案
文档属性
| 名称 | 北师大版2019_2020学年九年级数学下册第三章圆检测卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 426.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 07:55:22 | ||
图片预览




文档简介
第 三 章 单元检测卷
一.选择题(共11小题)
1.下列说法错误的是( )
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
2.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
(第2题图)
A. B. C. D.
3.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
(第3题图)
A.3cm B. cm C.2.5cm D. cm
4.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
(第4题图)
A.50° B.60° C.80° D.100°
5.如图,已知⊙O的半径为5,AB是⊙O的弦,AB=8,Q为AB中点,P是圆上的一点(不与A、B重合),连接PQ,则PQ的最小值为( )
(第5题图)
A.1 B.2 C.3 D.8
6.如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
(第6题图)
A.30° B.35° C.40° D.50°
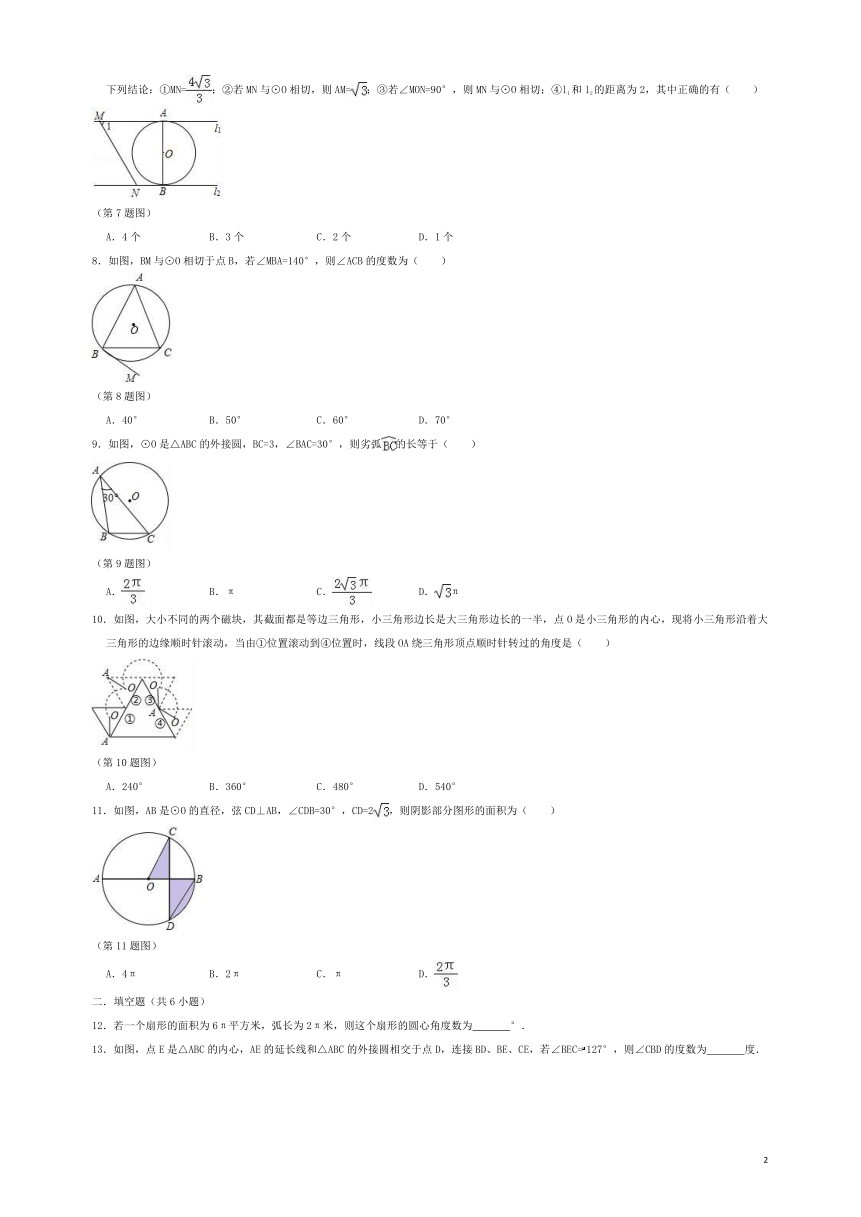
7.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=;②若MN与⊙O相切,则AM=;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
(第7题图)
A.4个 B.3个 C.2个 D.1个
8.如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
(第8题图)
A.40° B.50° C.60° D.70°
9.如图,⊙O是△ABC的外接圆,BC=3,∠BAC=30°,则劣弧的长等于( )
(第9题图)
A. B.π C. D.π
10.如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕三角形顶点顺时针转过的角度是( )
(第10题图)
A.240° B.360° C.480° D.540°
11.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分图形的面积为( )
(第11题图)
A.4π B.2π C.π D.
二.填空题(共6小题)
12.若一个扇形的面积为6π平方米,弧长为2π米,则这个扇形的圆心角度数为 °.
13.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠BEC=127°,则∠CBD的度数为 度.
(第13题图)
14.如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是 .
(第14题图)
15.如图,⊙O的内接五边形ABCDE的对角线AC与BD相交于点G,若∠E=92°,∠BAC=41°,则∠DGC= °.
(第15题图)
16.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,AD与BC相交于点F,连结BE,DC,已知EF=2,CD=5,则AD= .
(第16题图)
17.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC= (用p、q表示).
(第17题图)
三.解答题(共8小题)
18.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
(第18题图)
19.如图,AB是⊙O的直径,BC交⊙O于点D,E是的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
(第19题图)
20.如图,AB为⊙O的直径,弦AC=2,∠ABC=30°,∠ACB的平分线交⊙O于点D,求:
(1)BC、AD的长;
(2)图中两阴影部分面积的和.
(第20题图)
21.如图,AB是⊙O的直径,CE⊥AB于E,弦AD交CE延长线于点F,CF﹦AF.
(1)求证: =;
(2)若BC=8,tan∠DAC=,求⊙O的半径.
(第21题图)
22.如图直角坐标系中,已知A(﹣8,0),B(0,6),点M在线段AB上.
(1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由;
(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.
(第22题图)
23.如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C.
(1)写出图中所有的全等三角形;
(2)已知PA=4,PD=2,求⊙O的半径.
(第23题图)
24.已知:如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O的半径为5,∠BAC=60°,求DE的长.
(第24题图)
25.如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=DH,∠COD=23°,求∠P的度数.
(第25题图)
参考答案
一. 1.B 2.A 3.D 4.D 5.B 6.C 7.B 8.A 9.B 10. C 11.D
二.12.【解答】设扇形圆心角的度数为n,半径为r,
∵扇形的弧长为2π,面积为6π,
∴6π=×2πr,解得r=6.
∵=2π,
∴n=60°.
故答案为:60.
13.【解答】∵点E是△ABC的内心,
∴∠BEC=90°+∠BAC,
∴∠BAC=74°,
∴∠DAC=∠BAC=37°,
∴∠CBD=∠DAC=37°.
故答案为37.
14.【解答】如图,连接OA,
∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴AD=AB=30cm,
∴设半径为r,则OD=r﹣10,
根据题意,得r2=(r﹣10)2+302,
解得r=50.
∴这个车轮的外圆半径长为50cm.
故答案为:50cm.
15.【解答】∵∠E+∠ABD=180°,∠E=92°,
∴∠ABD=88°,
∵∠BAC=41°,
∴∠AGB=180°﹣∠ABG﹣∠BAC=180°﹣88°﹣41°=51°,
∵∠DGC=∠AGB,
∴∠DGC=51°.
故答案为51°.
16.【解答】∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∴=,
∴BD=CD=5,
由圆周角定理,得∠CAD=∠CBD,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠CAD,
∴∠DBE=∠DEB.
∴DE=DB=5,
∴DF=DE﹣EF=3,
∵∠DBC=∠BAD,∠BDF=∠ADB,
∴△BDF∽△ADB,
∴=,
∴AD==,
故答案为:.
17.【解答】延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.
∵AB∥CD
∴=,
∴BC=AE=q.
在△ACE中,∠CAE=90°,CE=2p,AE=q,
故AC==.
三. 18.解:连接OD,
∵OA=OD,∠A=45°,
∴∠A=∠ADO=45°,
∴∠DOB=90°,即OD⊥AB,
∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2
∴S梯形OBCD===,
∴图中阴影部分的面积S=S梯形OBCD﹣S扇形OBD=﹣=﹣.
19.(1)证明:连结AD,如图,
∵E是的中点,
∴==,
∴∠EAB=∠EAD,
∵∠ACB=2∠EAB,
∴∠ACB=∠DAB,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAC+∠ACB=90°,
∴∠DAC+∠DAB=90°,即∠BAC=90°,
∴AC⊥AB,
∴AC是⊙O的切线;
(2)①在Rt△ACB中,
∵cosC===,AC=6,
∴BC=9.
②作FH⊥AB于H,
∵BD=BC﹣CD=5,∠EAB=∠EAD,FD⊥AD,FH⊥AB,
∴FD=FH,设FB=x,则DF=FH=5﹣x,
∵FH∥AC,
∴∠HFB=∠C,
在Rt△BFH中,
∵cos∠BFH=cos∠C==,
∴=,
解得x=3,即BF的长为3,
∴DF=2
20.解:(1)∵AB是直径,
∴∠ACB=∠ADB=90°(直径所对的圆周角是直角),
在Rt△ABC中,∠ABC=30°,AC=2,
∴AB=4,
∴BC==2,
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD
∴=,
∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=2;
(2)连接OC,OD,
∵∠ABC=30°,
∴∠AOC=∠2∠ABC=60°,
∵OA=OB,
∴S△AOC=S△ABC=××AC×BC=××2×2=,
由(1)得∠AOD=90°,
∴∠COD=150°,
S△AOD=×AO×OD=×22=2,
∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=﹣﹣2=π﹣﹣2.
21.(1)证明:延长CF交⊙O于H,连接AH,
∵CE⊥AB,
∴=,
∵CF﹦AF,
∴∠FAC=∠FCA,
∴=,
∴=;
(2)解:∵=,
∴∠B=∠DAC,
∴tanB=,即=,
解得AC=8,
∴AB==16,
∴⊙O的半径为8.
22.解:(1)直线OB与⊙M相切,
理由:设线段OB的中点为D,连结MD,如图1,
∵点M是线段AB的中点,所以MD∥AO,MD=4.
∴∠AOB=∠MDB=90°,
∴MD⊥OB,点D在⊙M上,
又∵点D在直线OB上,
∴直线OB与⊙M相切;
(2)解:连接ME,MF,如图2,
∵A(﹣8,0),B(0,6),
∴设直线AB的解析式是y=kx+b,
∴,
解得k=,b=6,
即直线AB的函数关系式是y=x+6,
∵⊙M与x轴、y轴都相切,
∴点M到x轴、y轴的距离都相等,即ME=MF,
设M(a,﹣a)(﹣8<a<0),
把x=a,y=﹣a代入y=x+6,
得﹣a=a+6,得a=﹣,
∴点M的坐标为(﹣,).
23.解:(1)△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP;
(2)设⊙O的半径为r,则OA=OD=r,
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在Rt△OAP中,∵OA2+PA2=OP2,
∴r2+42=(r+2)2,
解得r=3,
即⊙O的半径为3.
24.(1)证明:如图1,连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,又DC=BD,
∴AB=AC;
(2)证明:如图2,连接OD,
∵AO=BO,CD=DB,
∴OD是△ABC的中位线,
∴OD∥AC,又DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线;
(3)解:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴BC=AC=10,
∴CD=5,
∵△ABC是等边三角形,
∴∠C=60°,
在Rt△DEC中,DE=CD×sinC=.
25.(1)证明:如图1,
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∵∠ABC=90°,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,
∵AB=DH,
∴tan∠ACB==,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=(180°﹣23°)=()°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=()°,
∵PC=PB,
∴∠P=180°﹣2×()°=97°.
PAGE
12
