2019年人教版数学八年级下册19.2.2 一次函数第一课时同步练习(含答案)
文档属性
| 名称 | 2019年人教版数学八年级下册19.2.2 一次函数第一课时同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 15:50:20 | ||
图片预览


文档简介
19.2.2 一次函数
基础闯关全练
1.下列函数关系式:①y=-x;②y=2x+11;③y=x?+x+1;④y=,其中一次函数的个数是 ( )
A.1
B.2
C.3
D.4
2.函数y-(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
A.m≠2
B.m≠-1
C.m=-1
D.m≠2且m≠-1
3.(2018湖南湘西中考)一次函数y=-2x+3的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.(2018甘肃酒泉中考)在平面直角坐标系中,一次函数y=kx+b的图象如图19-2-2-1-1所示,观察图象可得( )
A.k>0,b>0
B.k>0,b<0
C.k<O,b>0
D.k<0,b<0
5.(2018湖南邵阳一模)一次函数y=kx+2(k为常数,且k≠0)的图象如图19-2-2-1-2所示,则k的可能值为_______.(写出一个即可)
能力提升全练
1.(2018山东肥城期末)已知一次函数y=kx-m-2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0
B.k<2,m<0
C.k>2,m>0
D.k>2,m<0
2.(2018广东深圳中考)把函数y=x向上平移3个单位长度,下列点在该平移后的直线上的是( )
A.(2,2)
B.(2,3)
C.(2,4)
D.(2,5)
3.(2018浙江绍兴中考)如图19-2-2-1-3,一个函数的图象由射线BA、线段BC、射线CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数( )
A.当x<1时,y随x的增大而增大
B.当x<1时,y随x的增大而减小
C.当x>1时,y随x的增大而增大
D.当x>1时,y随x的增大而减小
三年模拟全练
一、选择题
1.(2018河南洛阳洛宁期中,4,★☆☆)下列函数关系式:①y=-2x+1;②y=x;③y=2x?+1;④y=,其中一次函数有( )
A.1个
B.2个
C.3个
D.4个
2.(2018福建龙岩期末,7,★☆☆)关于函数y=-2x+1,下列结论正确的是( )
A.图象必经过点(-2,1)
B.图象经过第一、二、三象限
C.当x>时,y<0
D. y随x的增大而增大
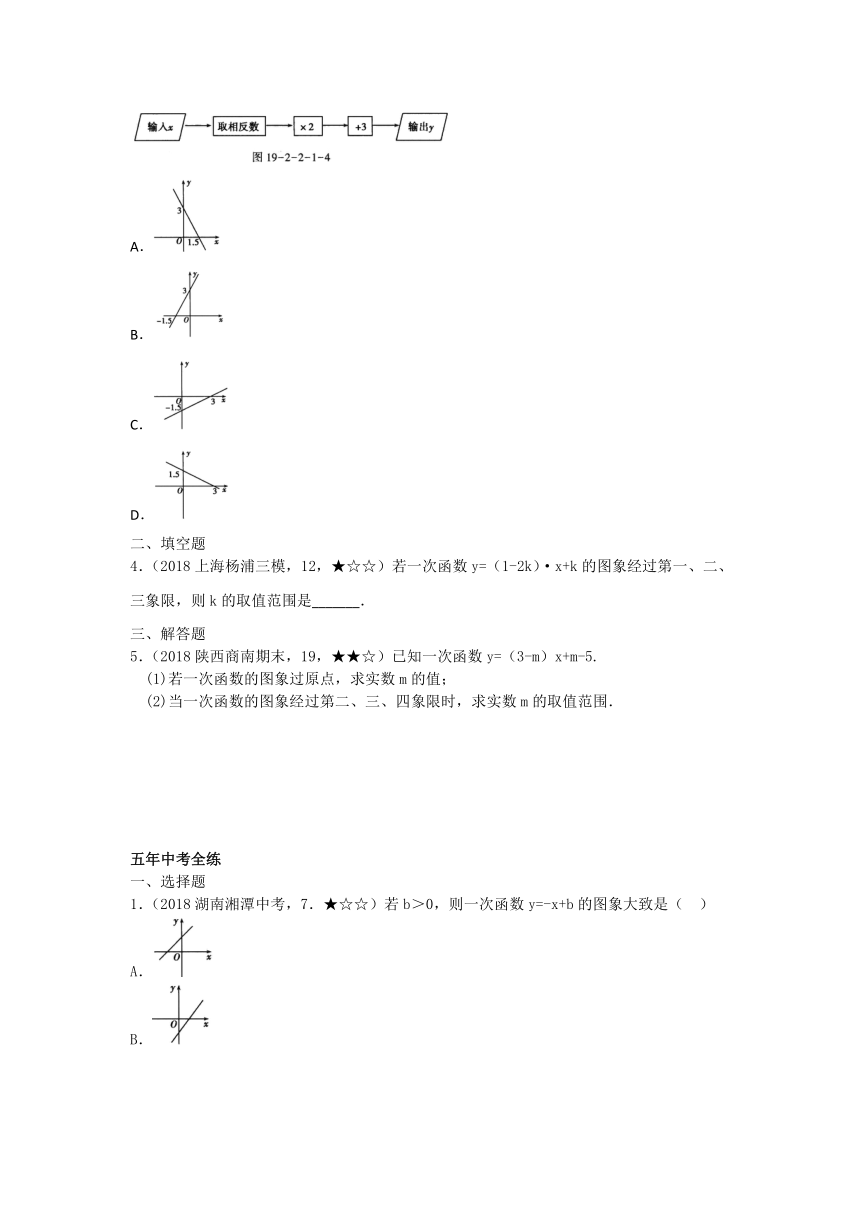
3.(2018河北邢台期末.9.★★☆)在如图19-2-2-1-4所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
二、填空题
4.(2018上海杨浦三模,12,★☆☆)若一次函数y=(1-2k)·x+k的图象经过第一、二、三象限,则k的取值范围是_______.
三、解答题
5.(2018陕西商南期末,19,★★☆)已知一次函数y=(3-m)x+m-5.
(1)若一次函数的图象过原点,求实数m的值;
(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
五年中考全练
一、选择题
1.(2018湖南湘潭中考,7.★☆☆)若b>0,则一次函数y=-x+b的图象大致是( )
A.
B.
C.
D.
2.(2017浙江温州中考.6.★☆☆)已知点(-1,y?),(4,y?)在一次函数y=3x-2的图象上,则y?,y?,0的大小关系是 ( )
A.O<y?<y?
B.y?<O<y?
C.y?<y?<0
D.y?<O<y?
二、填空题
3.(2018天津中考,16,★☆☆)将直线y=x向上平移2个单位长度,平移后直线的解析式为_______.
4.(2018山东济宁中考.12,★☆☆)在平面直角坐标系中,已知一次函数y=-2x+1的图象经过P?(x?,y?.),P?(x?,y?)两点,若x?<x?,则y?_______y?(填“>”“<”或“=”).
5.(2018四川宜宾中考,12,★☆☆)已知点A是直线y=x+1上一点,其横坐标为-,若点B与点A关于y轴对称,则点B的坐标为_________.
核心素养全练
1.已知关于x的一次函数y=(a+3)x+(b-2).
(1)当a为何值时,y随x的增大而减小?
(2)当a,b为何值时,函数图象与y轴的交点在x轴上方?
(3)当a,b为何值时,函数图象经过第一、三、四象限?
(4)当a,b为何值时,函数图象经过原点?
(5)当a,b为何值时,函数的图象与直线y=-3x平行?
2.一次函数y=(m-2)x+m?-1的图象经过点A(0,3).
(1)求m的值,并写出函数解析式;
(2)若(1)中的函数图象与x轴交于点B,直线y=(n+2)x+n?-1也经过点A(0,3),且与x轴交于点C,求线段BC的长.
19.2.2一次函数(1)
1.B①y=-x是一次函数;②y=2x+11是一次函数;③④不符合一次函数的定义,故不是一次函数,故选B.
2.A根据一次函数的定义知,一次项系数不等于0.即m-2≠0.解得m≠2.
3.C ∵k=-2<0,
∴一次函数y=-2x+3的图象必过第二、四象限,
∴b=3,
∴函数图象交y轴于正半轴,
∴函数图象经过第一、二、四象限,不经过第三象限.故选C.
4.A由图象可知,直线从左往右呈上升趋势,故k>0,图象与y轴的交点在y轴正半轴上,故b>0.
5.答案 -2(答案不唯一)
解析 观察图象可知,OB<OA,k<0.
当x=0时,y=kx+2=2,∴OA=2,
令OB=1.则点B(1,0),将(1,0)代入y=kx+2,得0=k+2,解得k=-2.
1.A整理得y=(k-2)x-m,因为函数图象与y轴负半轴相交,所以-m<0.即m>0,又函数值y随x的增大而减小,所以k-2<0.即k<2.故选A.
2.D 一次函数的平移规律是“左加右减,上加下减”,故把函数y=x向上平移3个单位长度后的函数关系式为y=x+3,当x=2时.y=2+3=5.故选D.
3.A由函数图象可知,当x<1时,y随x的增大而增大,因此A正确,B错误;当1<x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大,因此C、D错误,故选A.
一、选择题
1.B ①y=-2x+1和②y=x是一次函数,③④不符合一次函数的定义.故选B.
2.C ∵k<0,所以y随x的增大而减小,故D错误;∵k<0,b>0,∴图象经过一、二、四象限,故B错误;当x=-2时,y=4+1=5,故A错误.故选C.
3.A由题意得y=-2x+3,所以当x=0时,y=3;当y=0时,x=1.5,即图象经过点(0,3)和点(1.5,0),选项A符合要求,故选A.
二、填空题
4.答案0<k<
解析 ∵一次函数y=(1-2k)x+k的图象经过第一、二、三象限,∴∴0<k<.
三、解答题
5.解析(1)∵一次函数图象过原点,
∴
解得m=5.
(2)∵一次函数的图象经过第二、三、四象限,
∴3<m<5.
一、选择题
1.C对于一次函数y=kx+b(k≠0),当k>0时,图象从左到右上升;当k<0时,图象从左到右下降;当b>0时,图象与y轴的交点在y轴正半轴;当b=0时,图象与y轴的交点在原点;当b<0时,图象与y轴的交点在y轴负半轴∵-1<0,∴图象从左到右下降,又b>0,∴图象与y轴的交点在y轴正半轴,故选C.
2.B解法一:将x=-1代入y=3x-2,得y=-5,∴y?=-5;将x=4代入y=3x-2,得y=10,∴y?=10,所以y?<O<y?.故选B.
解法二:∵k=3>0,∴y随x的增大而增大,易知x=时,y=0,又-1<<4,∴y?<0<y?,故选B.
二、填空题
3.答案y=x+2
解析 由平移规律“左加右减,上加下减”,可知向上平移2个单位长度后,直线的解析式为y=x+2.
4.答案 >
解析 一次函数y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小,因为y=-2x+1中的k=-2<0,所以当x?<x?时,y?>y?.
5.答案()
解析把x=-代入y=x+1得y=,∴点A的坐标为(-),∵点8和点A关于y轴对称,∴点B的坐标为().
1.解析(1)由一次函数的性质可知,当a+3<0,即a<-3时,y随x的增大而减小.
(2)由题意知,当a+3≠0且b-2>0时,即当a≠-3且b>2时,函数图象与y轴的交点在x轴上方.
(3)因为函数图象经过第一、三、四象限,所以a+3>0且b-2<0.所以a>-3且b<2,即当a>-3且b<2时,函数图象经过第一、三、四象限.
(4)由题意,得a+3≠0且b-2=0,解得a≠-3且b=2.即当a≠-3且b=2时,函数图象经过原点.
(5)由题意,得a+3=-3且b-2≠0,解得a=-6且b≠2.所以当a=-6且b≠2时,函数图象与直线y=-3x平行.
2.解析(1)由题意得m?-1=3,
所以m=±2.
又m-2≠0,即m≠2,
所以m=-2,所以y=-4x+3.
(2)由题意可得B点的坐标为(,0).
因为直线y=(n+2)x+n?-1经过点A(0,3),
所以n?-1=3,所以n=±2.
又n+2≠0.即n≠-2.所以n=2.
所以y=4x+3,
所以C点的坐标为(-,0).
所以BC=.
基础闯关全练
1.下列函数关系式:①y=-x;②y=2x+11;③y=x?+x+1;④y=,其中一次函数的个数是 ( )
A.1
B.2
C.3
D.4
2.函数y-(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
A.m≠2
B.m≠-1
C.m=-1
D.m≠2且m≠-1
3.(2018湖南湘西中考)一次函数y=-2x+3的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.(2018甘肃酒泉中考)在平面直角坐标系中,一次函数y=kx+b的图象如图19-2-2-1-1所示,观察图象可得( )
A.k>0,b>0
B.k>0,b<0
C.k<O,b>0
D.k<0,b<0
5.(2018湖南邵阳一模)一次函数y=kx+2(k为常数,且k≠0)的图象如图19-2-2-1-2所示,则k的可能值为_______.(写出一个即可)
能力提升全练
1.(2018山东肥城期末)已知一次函数y=kx-m-2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
A.k<2,m>0
B.k<2,m<0
C.k>2,m>0
D.k>2,m<0
2.(2018广东深圳中考)把函数y=x向上平移3个单位长度,下列点在该平移后的直线上的是( )
A.(2,2)
B.(2,3)
C.(2,4)
D.(2,5)
3.(2018浙江绍兴中考)如图19-2-2-1-3,一个函数的图象由射线BA、线段BC、射线CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数( )
A.当x<1时,y随x的增大而增大
B.当x<1时,y随x的增大而减小
C.当x>1时,y随x的增大而增大
D.当x>1时,y随x的增大而减小
三年模拟全练
一、选择题
1.(2018河南洛阳洛宁期中,4,★☆☆)下列函数关系式:①y=-2x+1;②y=x;③y=2x?+1;④y=,其中一次函数有( )
A.1个
B.2个
C.3个
D.4个
2.(2018福建龙岩期末,7,★☆☆)关于函数y=-2x+1,下列结论正确的是( )
A.图象必经过点(-2,1)
B.图象经过第一、二、三象限
C.当x>时,y<0
D. y随x的增大而增大
3.(2018河北邢台期末.9.★★☆)在如图19-2-2-1-4所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
二、填空题
4.(2018上海杨浦三模,12,★☆☆)若一次函数y=(1-2k)·x+k的图象经过第一、二、三象限,则k的取值范围是_______.
三、解答题
5.(2018陕西商南期末,19,★★☆)已知一次函数y=(3-m)x+m-5.
(1)若一次函数的图象过原点,求实数m的值;
(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
五年中考全练
一、选择题
1.(2018湖南湘潭中考,7.★☆☆)若b>0,则一次函数y=-x+b的图象大致是( )
A.
B.
C.
D.
2.(2017浙江温州中考.6.★☆☆)已知点(-1,y?),(4,y?)在一次函数y=3x-2的图象上,则y?,y?,0的大小关系是 ( )
A.O<y?<y?
B.y?<O<y?
C.y?<y?<0
D.y?<O<y?
二、填空题
3.(2018天津中考,16,★☆☆)将直线y=x向上平移2个单位长度,平移后直线的解析式为_______.
4.(2018山东济宁中考.12,★☆☆)在平面直角坐标系中,已知一次函数y=-2x+1的图象经过P?(x?,y?.),P?(x?,y?)两点,若x?<x?,则y?_______y?(填“>”“<”或“=”).
5.(2018四川宜宾中考,12,★☆☆)已知点A是直线y=x+1上一点,其横坐标为-,若点B与点A关于y轴对称,则点B的坐标为_________.
核心素养全练
1.已知关于x的一次函数y=(a+3)x+(b-2).
(1)当a为何值时,y随x的增大而减小?
(2)当a,b为何值时,函数图象与y轴的交点在x轴上方?
(3)当a,b为何值时,函数图象经过第一、三、四象限?
(4)当a,b为何值时,函数图象经过原点?
(5)当a,b为何值时,函数的图象与直线y=-3x平行?
2.一次函数y=(m-2)x+m?-1的图象经过点A(0,3).
(1)求m的值,并写出函数解析式;
(2)若(1)中的函数图象与x轴交于点B,直线y=(n+2)x+n?-1也经过点A(0,3),且与x轴交于点C,求线段BC的长.
19.2.2一次函数(1)
1.B①y=-x是一次函数;②y=2x+11是一次函数;③④不符合一次函数的定义,故不是一次函数,故选B.
2.A根据一次函数的定义知,一次项系数不等于0.即m-2≠0.解得m≠2.
3.C ∵k=-2<0,
∴一次函数y=-2x+3的图象必过第二、四象限,
∴b=3,
∴函数图象交y轴于正半轴,
∴函数图象经过第一、二、四象限,不经过第三象限.故选C.
4.A由图象可知,直线从左往右呈上升趋势,故k>0,图象与y轴的交点在y轴正半轴上,故b>0.
5.答案 -2(答案不唯一)
解析 观察图象可知,OB<OA,k<0.
当x=0时,y=kx+2=2,∴OA=2,
令OB=1.则点B(1,0),将(1,0)代入y=kx+2,得0=k+2,解得k=-2.
1.A整理得y=(k-2)x-m,因为函数图象与y轴负半轴相交,所以-m<0.即m>0,又函数值y随x的增大而减小,所以k-2<0.即k<2.故选A.
2.D 一次函数的平移规律是“左加右减,上加下减”,故把函数y=x向上平移3个单位长度后的函数关系式为y=x+3,当x=2时.y=2+3=5.故选D.
3.A由函数图象可知,当x<1时,y随x的增大而增大,因此A正确,B错误;当1<x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大,因此C、D错误,故选A.
一、选择题
1.B ①y=-2x+1和②y=x是一次函数,③④不符合一次函数的定义.故选B.
2.C ∵k<0,所以y随x的增大而减小,故D错误;∵k<0,b>0,∴图象经过一、二、四象限,故B错误;当x=-2时,y=4+1=5,故A错误.故选C.
3.A由题意得y=-2x+3,所以当x=0时,y=3;当y=0时,x=1.5,即图象经过点(0,3)和点(1.5,0),选项A符合要求,故选A.
二、填空题
4.答案0<k<
解析 ∵一次函数y=(1-2k)x+k的图象经过第一、二、三象限,∴∴0<k<.
三、解答题
5.解析(1)∵一次函数图象过原点,
∴
解得m=5.
(2)∵一次函数的图象经过第二、三、四象限,
∴3<m<5.
一、选择题
1.C对于一次函数y=kx+b(k≠0),当k>0时,图象从左到右上升;当k<0时,图象从左到右下降;当b>0时,图象与y轴的交点在y轴正半轴;当b=0时,图象与y轴的交点在原点;当b<0时,图象与y轴的交点在y轴负半轴∵-1<0,∴图象从左到右下降,又b>0,∴图象与y轴的交点在y轴正半轴,故选C.
2.B解法一:将x=-1代入y=3x-2,得y=-5,∴y?=-5;将x=4代入y=3x-2,得y=10,∴y?=10,所以y?<O<y?.故选B.
解法二:∵k=3>0,∴y随x的增大而增大,易知x=时,y=0,又-1<<4,∴y?<0<y?,故选B.
二、填空题
3.答案y=x+2
解析 由平移规律“左加右减,上加下减”,可知向上平移2个单位长度后,直线的解析式为y=x+2.
4.答案 >
解析 一次函数y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小,因为y=-2x+1中的k=-2<0,所以当x?<x?时,y?>y?.
5.答案()
解析把x=-代入y=x+1得y=,∴点A的坐标为(-),∵点8和点A关于y轴对称,∴点B的坐标为().
1.解析(1)由一次函数的性质可知,当a+3<0,即a<-3时,y随x的增大而减小.
(2)由题意知,当a+3≠0且b-2>0时,即当a≠-3且b>2时,函数图象与y轴的交点在x轴上方.
(3)因为函数图象经过第一、三、四象限,所以a+3>0且b-2<0.所以a>-3且b<2,即当a>-3且b<2时,函数图象经过第一、三、四象限.
(4)由题意,得a+3≠0且b-2=0,解得a≠-3且b=2.即当a≠-3且b=2时,函数图象经过原点.
(5)由题意,得a+3=-3且b-2≠0,解得a=-6且b≠2.所以当a=-6且b≠2时,函数图象与直线y=-3x平行.
2.解析(1)由题意得m?-1=3,
所以m=±2.
又m-2≠0,即m≠2,
所以m=-2,所以y=-4x+3.
(2)由题意可得B点的坐标为(,0).
因为直线y=(n+2)x+n?-1经过点A(0,3),
所以n?-1=3,所以n=±2.
又n+2≠0.即n≠-2.所以n=2.
所以y=4x+3,
所以C点的坐标为(-,0).
所以BC=.
