1.1.1 柱、锥、台、球的结构特征 课件(17张PPT)
文档属性
| 名称 | 1.1.1 柱、锥、台、球的结构特征 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 00:00:00 | ||
图片预览



文档简介
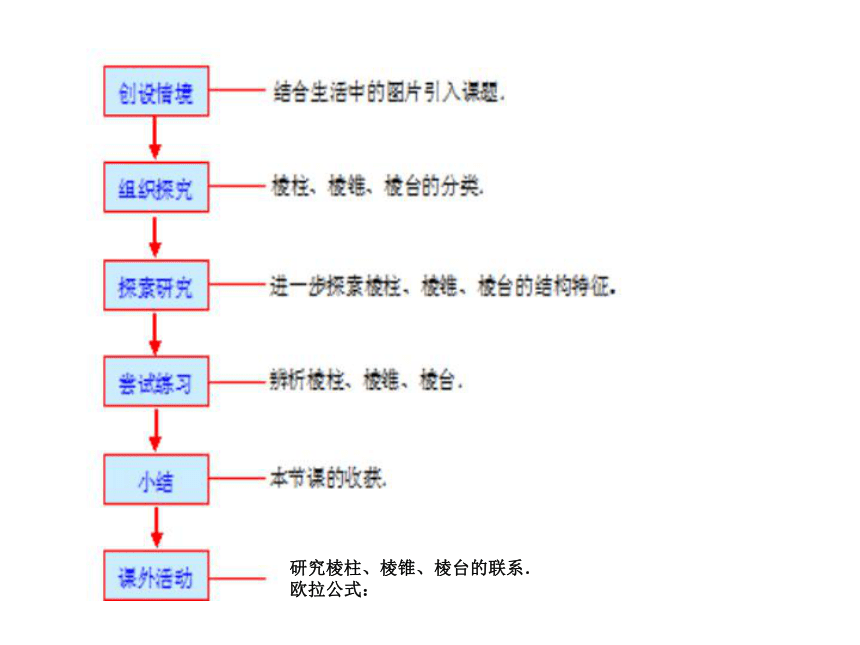
课件17张PPT。空间几何体棱柱、棱锥、棱台的结构特征高中数学必修2研究棱柱、棱锥、棱台的联系.
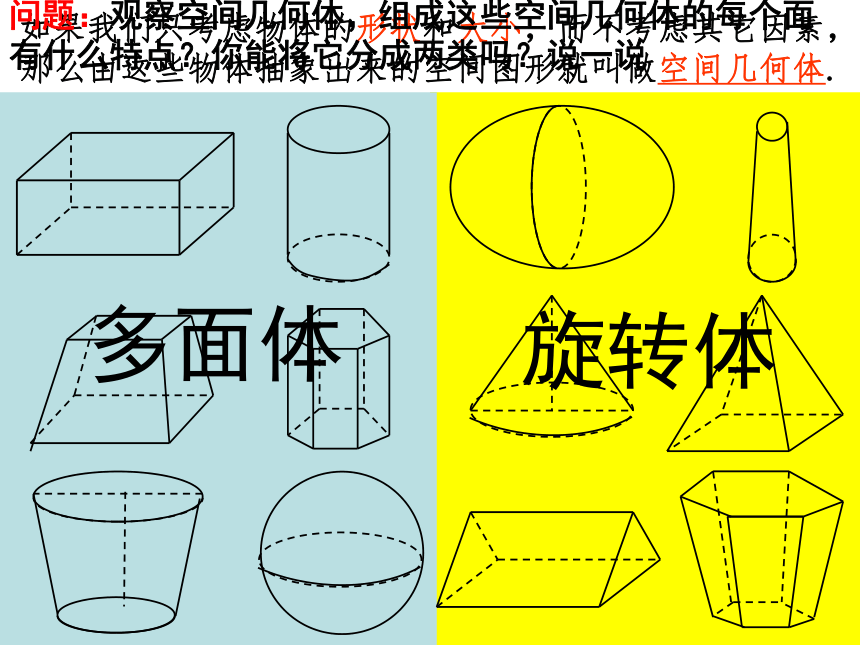
欧拉公式:知识探究(一)空间几何体及其类型如果我们只考虑物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.问题:观察空间几何体,组成这些空间几何体的每个面有什么特点?你能将它分成两类吗?说一说多面体旋转体多面体各构成要素的名称:面:围成多面体的各
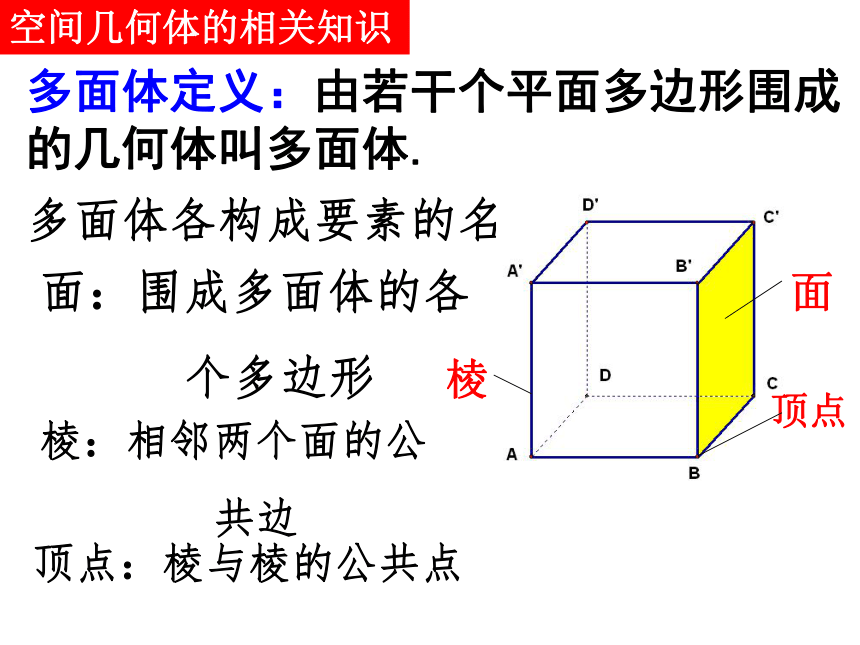
个多边形棱:相邻两个面的公
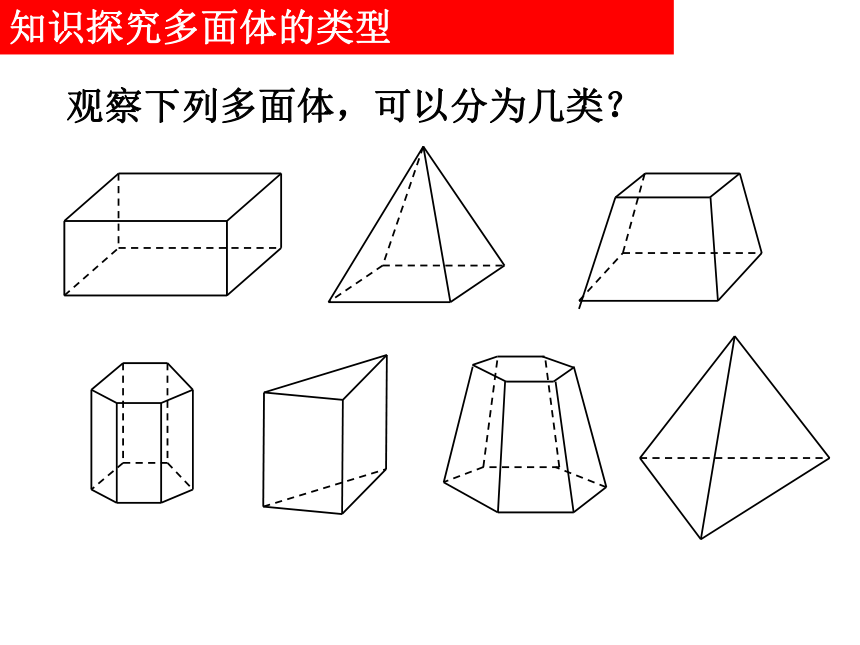
共边顶点:棱与棱的公共点多面体定义:由若干个平面多边形围成的几何体叫多面体.空间几何体的相关知识知识探究多面体的类型观察下列多面体,可以分为几类?知识探究(二)棱柱、棱锥、棱台的结构特征1. 下列几何体是棱柱的有( )课堂练习:2. 下面是几种常见的棱柱,如何在名称上区分这些棱柱?课堂练习:3.(1)用一个平行于棱锥底面的平面去截棱锥,截面与底面的形状关系如何?相似多边形(2)下列几何体是不是棱台,为什么?
4.(1)如图,过长方体的棱BC的截面截去长方体的一角,截去的几何体是什么?剩下的几何体是什么?你能说出它们的名称吗?
(2)长方体有几对面是平行的?哪些面可以作为它的上下底面?
(3)如图,六角螺母的空间结构特征,它有几对面是平行的?哪些面可以作为它的上下底面?
小结:通过本节课的学习,你有什么收获?棱柱、棱锥、棱台的结构特征课外研究性作业一.研究棱柱、棱锥、棱台的联系.
二.欧拉公式.
既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点探究一 观察下面有5个多面体,分别数出它们的顶点数V、 面数F和棱数E,并填出下表;4681268981599164612探究二
欧拉公式:知识探究(一)空间几何体及其类型如果我们只考虑物体的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.问题:观察空间几何体,组成这些空间几何体的每个面有什么特点?你能将它分成两类吗?说一说多面体旋转体多面体各构成要素的名称:面:围成多面体的各
个多边形棱:相邻两个面的公
共边顶点:棱与棱的公共点多面体定义:由若干个平面多边形围成的几何体叫多面体.空间几何体的相关知识知识探究多面体的类型观察下列多面体,可以分为几类?知识探究(二)棱柱、棱锥、棱台的结构特征1. 下列几何体是棱柱的有( )课堂练习:2. 下面是几种常见的棱柱,如何在名称上区分这些棱柱?课堂练习:3.(1)用一个平行于棱锥底面的平面去截棱锥,截面与底面的形状关系如何?相似多边形(2)下列几何体是不是棱台,为什么?
4.(1)如图,过长方体的棱BC的截面截去长方体的一角,截去的几何体是什么?剩下的几何体是什么?你能说出它们的名称吗?
(2)长方体有几对面是平行的?哪些面可以作为它的上下底面?
(3)如图,六角螺母的空间结构特征,它有几对面是平行的?哪些面可以作为它的上下底面?
小结:通过本节课的学习,你有什么收获?棱柱、棱锥、棱台的结构特征课外研究性作业一.研究棱柱、棱锥、棱台的联系.
二.欧拉公式.
既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点探究一 观察下面有5个多面体,分别数出它们的顶点数V、 面数F和棱数E,并填出下表;4681268981599164612探究二
