人教新课标A版 必修2 第一章 空间几何体探究与发现 祖暅原理与柱体、椎体、球体的体积 24张
文档属性
| 名称 | 人教新课标A版 必修2 第一章 空间几何体探究与发现 祖暅原理与柱体、椎体、球体的体积 24张 |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 20:45:48 | ||
图片预览








文档简介
课件24张PPT。 祖暅,字景烁,祖冲之之子,范阳郡蓟县人(今河北省涞源县人),南北朝时代的伟大科学家。祖暅在数学上有突出贡献,他在实践的基础上,于5世纪末提出了体积的计算原理。祖暅原理:“幂势既同,则积不容异”。
“势”即是高,“幂”即是面积。祖暅原理 “幂势既同,则积不容异” 夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。祖暅原理 祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。祖冲之父子是
我们中华民族的
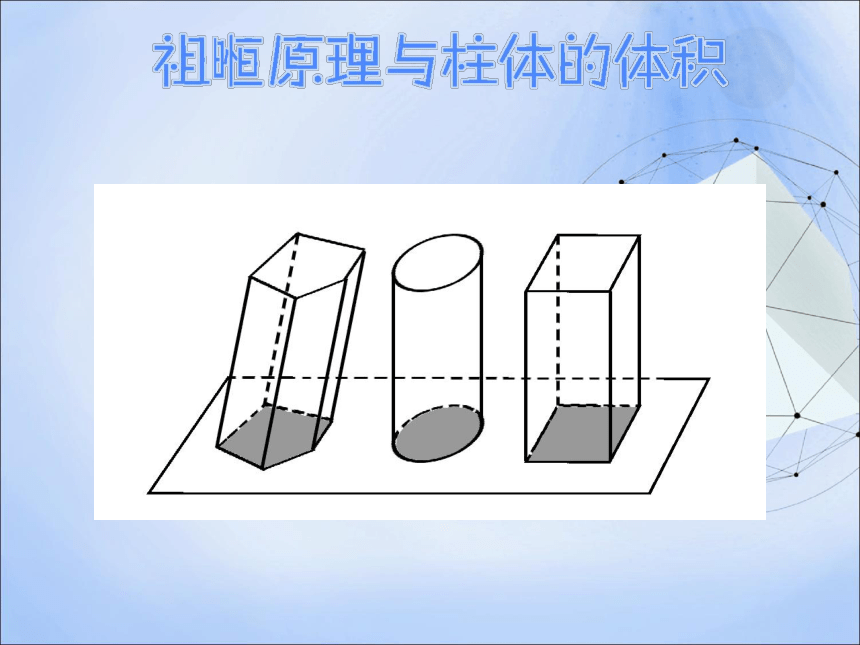
骄傲和自豪祖暅原理 “幂势既同,则积不容异” 设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一平面内。你能得到什么结论?由祖暅原理可得:
V柱体=Sh 其中S 是柱体的底面积,
h是柱体的高。例: 如图,是某几何体的三视图。由祖暅原理知:“幂势既同,则积不容异”。已知某不规则几何体与如图所示的几何体满足“幂势同”,求该不规则几何体的体积。(图中所给长度均为厘米)
解:所以某不规则几何体的体积是以8-π立方厘米 设有底面积都等于S,高都等于h的两个锥体(如图:一个棱锥和一个圆锥),使它们的下底面在同一平面内。你能得到什么结论?
等底面积等高的两个锥体的体积相等
如何把一个三棱柱分割成三个等体积的棱锥? 结论:对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。即
例:三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,求出该几何体的体积(图中的长度单位是厘米)。先研究半球的体积
思考:
如何找到一个与半球等体积的“替代品”呢?结论 半径为R的球 的体积公式是
例: 一个正四面体的所有棱长都是 厘米,四个顶点都在同一球面上,求此球的体积。课堂练习
某几何体的三视图如图,求该几何体的体积。
(图中所给数字单位为厘米)所以该几何体的体积是课堂小结
总结一下你在本节课中
获得的知识和学习心得
祖暅原理
柱、锥、球的体积公式
布置作业
例:三棱锥P-ABC三条侧棱两两互相垂直,且PA=1,PB=2,PC=3,求它外接球的体积。
2、三棱锥P-ABC中侧棱PA长为3且垂直于底面ABC,底面是边长为2的正三角形,求这个三棱锥外接球的体积。
课后探究
利用祖暅原理探究台体的体积公式。
球、柱、台、锥体体积之间的关系。谢谢各位点评指导
“势”即是高,“幂”即是面积。祖暅原理 “幂势既同,则积不容异” 夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。祖暅原理 祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。祖冲之父子是
我们中华民族的
骄傲和自豪祖暅原理 “幂势既同,则积不容异” 设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一平面内。你能得到什么结论?由祖暅原理可得:
V柱体=Sh 其中S 是柱体的底面积,
h是柱体的高。例: 如图,是某几何体的三视图。由祖暅原理知:“幂势既同,则积不容异”。已知某不规则几何体与如图所示的几何体满足“幂势同”,求该不规则几何体的体积。(图中所给长度均为厘米)
解:所以某不规则几何体的体积是以8-π立方厘米 设有底面积都等于S,高都等于h的两个锥体(如图:一个棱锥和一个圆锥),使它们的下底面在同一平面内。你能得到什么结论?
等底面积等高的两个锥体的体积相等
如何把一个三棱柱分割成三个等体积的棱锥? 结论:对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。即
例:三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,求出该几何体的体积(图中的长度单位是厘米)。先研究半球的体积
思考:
如何找到一个与半球等体积的“替代品”呢?结论 半径为R的球 的体积公式是
例: 一个正四面体的所有棱长都是 厘米,四个顶点都在同一球面上,求此球的体积。课堂练习
某几何体的三视图如图,求该几何体的体积。
(图中所给数字单位为厘米)所以该几何体的体积是课堂小结
总结一下你在本节课中
获得的知识和学习心得
祖暅原理
柱、锥、球的体积公式
布置作业
例:三棱锥P-ABC三条侧棱两两互相垂直,且PA=1,PB=2,PC=3,求它外接球的体积。
2、三棱锥P-ABC中侧棱PA长为3且垂直于底面ABC,底面是边长为2的正三角形,求这个三棱锥外接球的体积。
课后探究
利用祖暅原理探究台体的体积公式。
球、柱、台、锥体体积之间的关系。谢谢各位点评指导
