2.2 用样本估计总体 课件(24张PPT)
文档属性
| 名称 | 2.2 用样本估计总体 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 657.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 22:58:40 | ||
图片预览






文档简介
课件24张PPT。用样本数据
估计总体
问题:如何从频率分布直方图中估计众数、中位数、平均数? 众数
出现次数最多的数 平均数
一组数据的和除以数据个数所得到的数. 中位数
按大小顺序排列,处于中间位置的数1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如右图所示),则该样本的中位数、众数、极差分别是 (??A? )?A. 46,45,56
B. 46,45,53
C. 47,45,56
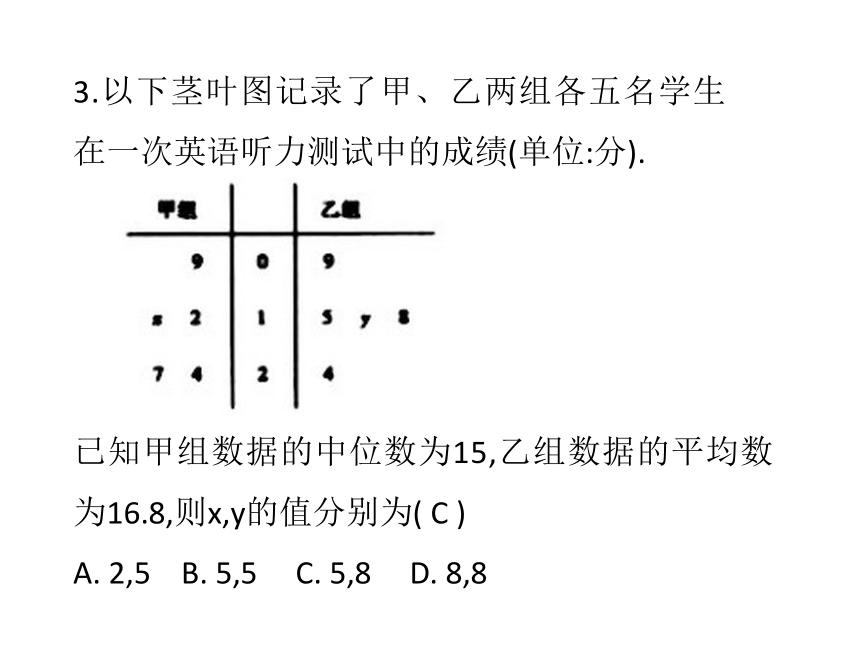
D. 45,47,533.以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( C )
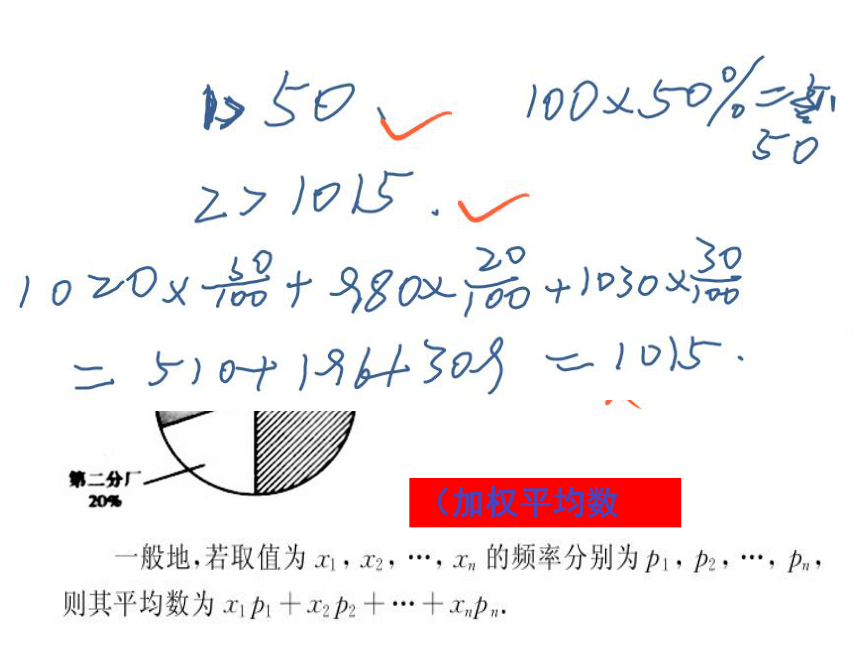
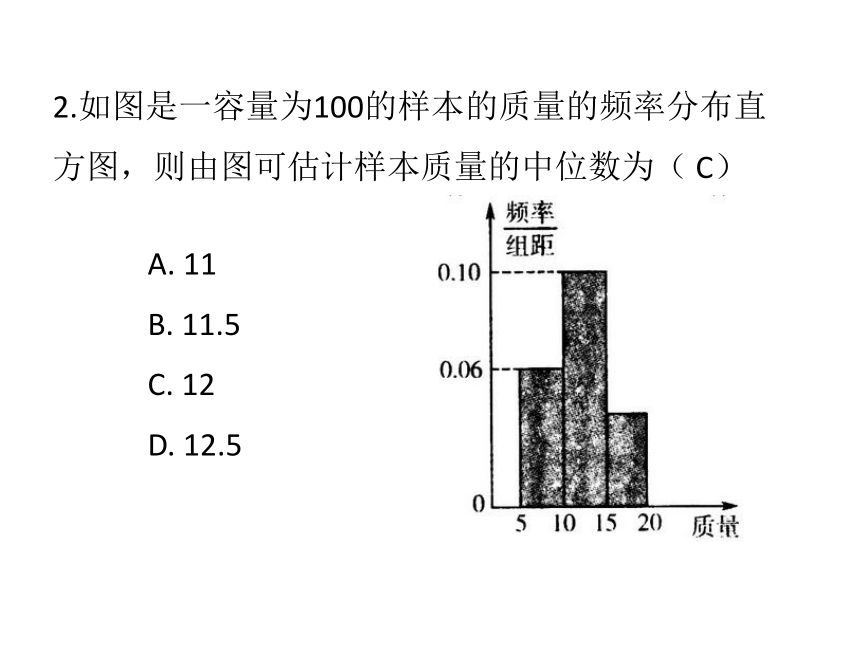
A.?2,5 B.?5,5 C.?5,8 D.?8,84某企业三个分厂生产同一种电子产品,三个分厂的产量分布如图所示,现在用分层抽样方法从三个分厂生产的产品中共抽取100件进行使用寿命的测试,则第一分厂应抽取的件数为 50 ;测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为1020小时,980小时,1030小时,估计这个企业生产的产品的平均使用寿命为 1015 小时.(加权平均数) 1020×50%+980×20%+1030×30%=1015小时2.如图是一容量为100的样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( C)A. 11
B. 11.5
C. 12
D. 12.52.某校在高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若[130,140]分数段的参赛学生人数为2.(1)求该校成绩在[90,140]分数段的参赛学生人数;
(2)估计90分以上(含90分)的学生成绩的众数、中位数和平均数(结果保留整数).问题:如何从频率分布直方图中估计众数、中位数、平均数? 众数
出现次数最多的数 估计众数
直方图面积最大的方条的横轴中点数字.(最高矩形的中点) 估计平均数
每个小矩形的面积╳小矩形底边中点的横坐标 之和. 平均数
一组数据的和除以数据个数所得到的数. 中位数
按大小顺序排列,处于中间位置的数 估计中位数
中位数把频率分布直方图分成左右两边面积相等.0.52.521.5143.534.5频率
组距2.250.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.022.02.........0.751.752.252.753.253.754.251.250.5 估计平均数
每个小矩形的面积╳小矩形底边中点的横坐标 之和.(加权平均数) 0.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.02提示:中位数左边的数据个数与右边的数据个数是相等的。0.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.02前四个小矩形的面积和=0.492.02 某射箭选手在伦敦奥运会上10箭的比赛成绩如下:
10,8,9,8,9,9,10,9,10,9:
(1)求出这组数据的众数、中位数、平均数。
(2)完成下表并绘制频率分布直方图;
(3)如何根据样本的频率分布直方图,估计总体的
众数、中位数和平均数。253100.20.50.20.30.50.3众数为9中点面积平分线中位数为9.10.5x=0.5-0.2
X=0.6面积为0.21089面积为0.2面积为0.5面积为0.38×0.2+9×0.5 +10×0.3=9.1平均数为9.1 问题:原始射箭成绩样本数据的众数是9,中位数是9,平均数是9.1,这与我们根据频率分布直方图得出的相应数据稍有偏差,如何解释一下原因。(1)频率分布直方图损失了一些样本数据,得到的众数、中位数和平均数是一个估计值,且所得估值与数据分组有关.(2)由不同的样本数据得到的众数、中位数和平均数,也会有偏差.例 (2015·广东)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.(1)求直方图中x的值;解 由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1得:x=0.007 5,
所以直方图中x的值是0.007 5.(2)求月平均用电量的众数和中位数;(2)求月平均用电量的
众数和中位数;因为
(0.002+0.009 5+0.011)×20=0.45<0.5,
所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5得:a=224,
所以月平均用电量的中位数是224.(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
解 月平均用电量为[220,240]的用户有0.012 5×20×100=25户,
月平均用电量[240,260)的用户有0.007 5×20×100=15户,
月平均用电量为[260,280)的用户有0.005×20×100=10户,月平均用电量为[280,300]的用户有0.002 5×20×100=5户, 根据样本频率分布直方图,可以估计总体的众数、中位数和平均数.每个小矩形的面积与小矩形底边中点的横坐标的乘积之和直方图面积的竖直平分线与横轴交点的横坐标最高矩形下端中点的横坐标 练习. 对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生参加社区服务的次数,根据此数据作出频率分布表和频率分布直方图如下(1)求出表中M,p及图中a的值;
(2)若该校高三学生240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计学生参加社区服务次数的众数、中位数及平均数.2.某校在高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若[130,140]分数段的参赛学生人数为2.(1)求该校成绩在[90,140]分数段的参赛学生人数;
(2)估计90分以上(含90分)的学生成绩的众数、中位数和平均数(结果保留整数).
出现次数最多的数 平均数
一组数据的和除以数据个数所得到的数. 中位数
按大小顺序排列,处于中间位置的数1.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如右图所示),则该样本的中位数、众数、极差分别是 (??A? )?A. 46,45,56
B. 46,45,53
C. 47,45,56
D. 45,47,533.以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( C )
A.?2,5 B.?5,5 C.?5,8 D.?8,84某企业三个分厂生产同一种电子产品,三个分厂的产量分布如图所示,现在用分层抽样方法从三个分厂生产的产品中共抽取100件进行使用寿命的测试,则第一分厂应抽取的件数为 50 ;测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为1020小时,980小时,1030小时,估计这个企业生产的产品的平均使用寿命为 1015 小时.(加权平均数) 1020×50%+980×20%+1030×30%=1015小时2.如图是一容量为100的样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( C)A. 11
B. 11.5
C. 12
D. 12.52.某校在高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若[130,140]分数段的参赛学生人数为2.(1)求该校成绩在[90,140]分数段的参赛学生人数;
(2)估计90分以上(含90分)的学生成绩的众数、中位数和平均数(结果保留整数).问题:如何从频率分布直方图中估计众数、中位数、平均数? 众数
出现次数最多的数 估计众数
直方图面积最大的方条的横轴中点数字.(最高矩形的中点) 估计平均数
每个小矩形的面积╳小矩形底边中点的横坐标 之和. 平均数
一组数据的和除以数据个数所得到的数. 中位数
按大小顺序排列,处于中间位置的数 估计中位数
中位数把频率分布直方图分成左右两边面积相等.0.52.521.5143.534.5频率
组距2.250.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.022.02.........0.751.752.252.753.253.754.251.250.5 估计平均数
每个小矩形的面积╳小矩形底边中点的横坐标 之和.(加权平均数) 0.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.02提示:中位数左边的数据个数与右边的数据个数是相等的。0.52.521.5143.534.5频率
组距0.040.080.150.220.250.140.060.040.02前四个小矩形的面积和=0.492.02 某射箭选手在伦敦奥运会上10箭的比赛成绩如下:
10,8,9,8,9,9,10,9,10,9:
(1)求出这组数据的众数、中位数、平均数。
(2)完成下表并绘制频率分布直方图;
(3)如何根据样本的频率分布直方图,估计总体的
众数、中位数和平均数。253100.20.50.20.30.50.3众数为9中点面积平分线中位数为9.10.5x=0.5-0.2
X=0.6面积为0.21089面积为0.2面积为0.5面积为0.38×0.2+9×0.5 +10×0.3=9.1平均数为9.1 问题:原始射箭成绩样本数据的众数是9,中位数是9,平均数是9.1,这与我们根据频率分布直方图得出的相应数据稍有偏差,如何解释一下原因。(1)频率分布直方图损失了一些样本数据,得到的众数、中位数和平均数是一个估计值,且所得估值与数据分组有关.(2)由不同的样本数据得到的众数、中位数和平均数,也会有偏差.例 (2015·广东)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.(1)求直方图中x的值;解 由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1得:x=0.007 5,
所以直方图中x的值是0.007 5.(2)求月平均用电量的众数和中位数;(2)求月平均用电量的
众数和中位数;因为
(0.002+0.009 5+0.011)×20=0.45<0.5,
所以月平均用电量的中位数在[220,240)内,
设中位数为a,
由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5得:a=224,
所以月平均用电量的中位数是224.(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
解 月平均用电量为[220,240]的用户有0.012 5×20×100=25户,
月平均用电量[240,260)的用户有0.007 5×20×100=15户,
月平均用电量为[260,280)的用户有0.005×20×100=10户,月平均用电量为[280,300]的用户有0.002 5×20×100=5户, 根据样本频率分布直方图,可以估计总体的众数、中位数和平均数.每个小矩形的面积与小矩形底边中点的横坐标的乘积之和直方图面积的竖直平分线与横轴交点的横坐标最高矩形下端中点的横坐标 练习. 对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生参加社区服务的次数,根据此数据作出频率分布表和频率分布直方图如下(1)求出表中M,p及图中a的值;
(2)若该校高三学生240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计学生参加社区服务次数的众数、中位数及平均数.2.某校在高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若[130,140]分数段的参赛学生人数为2.(1)求该校成绩在[90,140]分数段的参赛学生人数;
(2)估计90分以上(含90分)的学生成绩的众数、中位数和平均数(结果保留整数).
