2.2.1 用样本的频率分布估计总体分布 课件(23张PPT)
文档属性
| 名称 | 2.2.1 用样本的频率分布估计总体分布 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 22:55:17 | ||
图片预览






文档简介
课件23张PPT。2.2 用样本估计总体(1)
用样本的频率分布估计总体分布情境引入情境引入探究:如果标准太低,会影响居民的日常生活;如果标准太高,则不利于节水.
1、如果政府希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理?
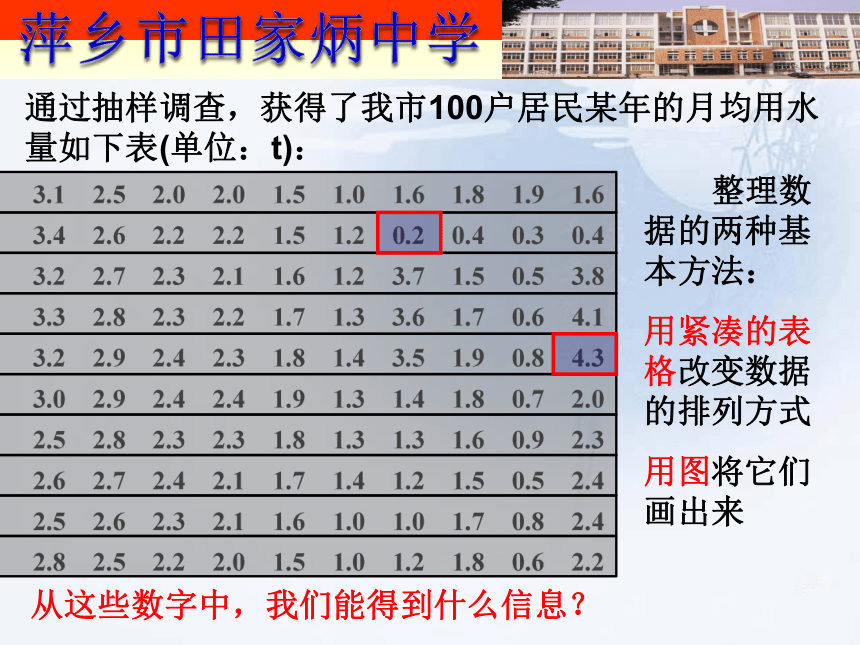
2、你认为,为了较合理地确定出这个标准,需要做哪些工作? 我市政府为了节约生活用水,计划在本市试行居民生活用水定额管理:即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费.从这些数字中,我们能得到什么信息? 整理数据的两种基本方法:
用紧凑的表格改变数据的排列方式
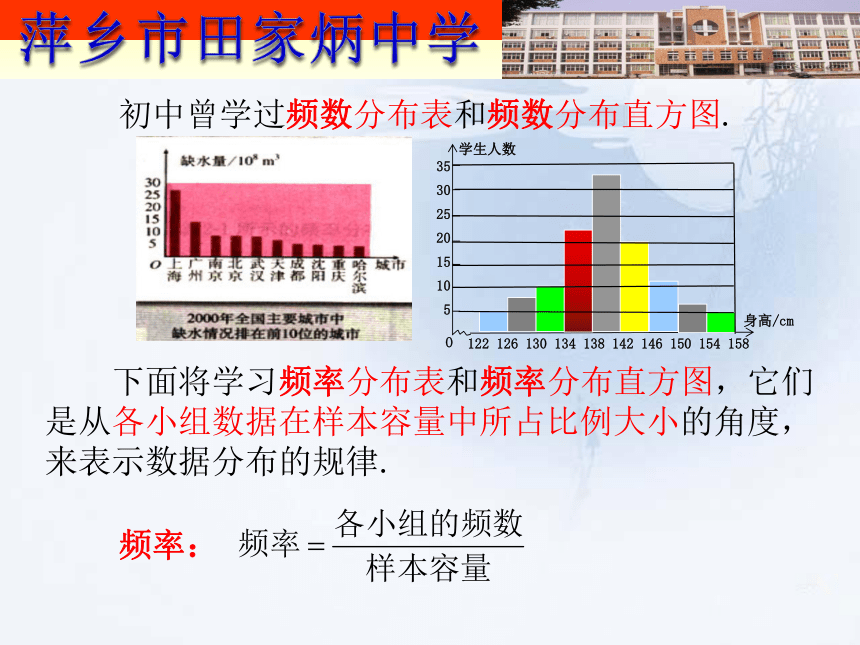
用图将它们画出来通过抽样调查,获得了我市100户居民某年的月均用水量如下表(单位:t): 初中曾学过频数分布表和频数分布直方图. 下面将学习频率分布表和频率分布直方图,它们是从各小组数据在样本容量中所占比例大小的角度,来表示数据分布的规律. 频率:知识探究1频率分布表第一步:求极差
数据中最大值与最小值的差.思考1:上述100个样本数据的变化范围是什么?4.3-0.2=4.1思考2:分成多少组合适呢?第二步:决定组距与组数 组距:每个小组两端点的距离;
组数:组数k=极差/组距
当数据在100个以内时, 按数据多少,常分5—12组;
若k不是整数,则组数=[k]+1.4.1÷0.5=8.2,故可取组数为9按组距为0.5进行分组,上述数据据共分为几组?第四步:列频率分布表
计算各小组的频率,列出下面的频率分布表.第三步:将数据分组[0,0.5),[0.5,1),[1,1.5),[1.5,2),
[2,2.5),[2.5,3),[3,3.5),[3.5,4),
[4,4.5]思考3:
如何设定各组数据的范围呢?各组均为左闭右开区间,
最后一组是闭区间思考4:
你能将这些数据用表格反映出来吗? 频率分布表一般分5列:
1、“分组”
2、“频数累计”(可省)
3、“频数”
4、“频率”
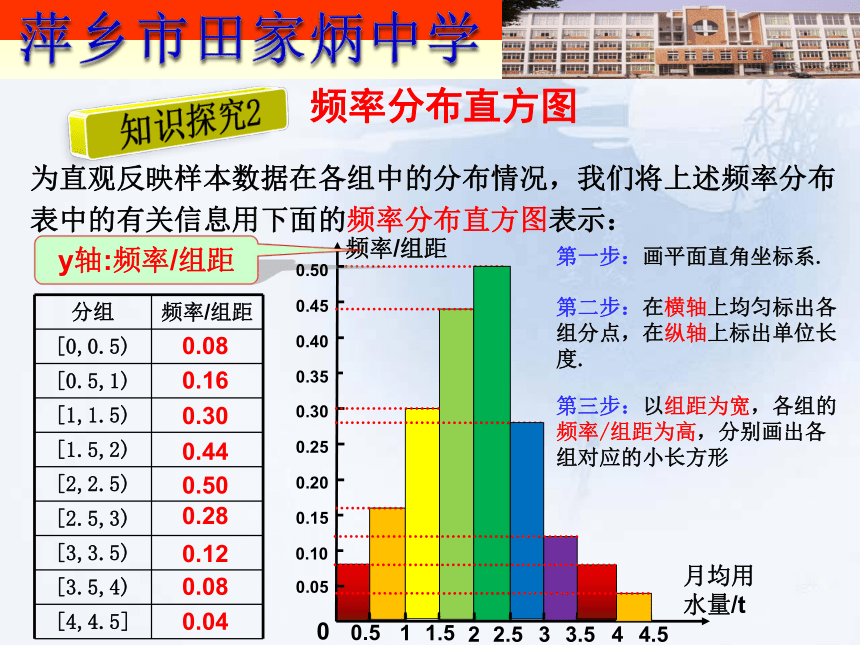
5、“频率/组距”列频率分布表:频数的合计为样本容量频率合计为148152225146420.040.080.150.220.250.140.060.041001.000.020.080.160.300.440.500.280.120.080.04为直观反映样本数据在各组中的分布情况,我们将上述频率分布表中的有关信息用下面的频率分布直方图表示: 月均用水量/t0.050.100.20频率/组距第一步:画平面直角坐标系. 第二步:在横轴上均匀标出各组分点,在纵轴上标出单位长度.第三步:以组距为宽,各组的频率/组距为高,分别画出各组对应的小长方形y轴:频率/组距知识探究2频率分布直方图0.40011.52.53.52340.54.50.150.250.300.350.450.500.080.160.300.440.500.280.120.080.041、各组频率在图中怎么显示出来?长方形的面积=3、你能根据上述频率分布直方图,指出样本居民月均用水量的一些数据特点吗?2、各小长方体面积之和是否为定值? 各小长方形的面积之和为1.思考6:同一组数据,若组距不同,得到的条形图会不会相同?思考5:如果市政府希望85%以上的居民月用水量不超过标准,根据上述频率分布直方图,你对制定居民月用水量标准(即a的取值)有何建议? 在频率分布直方图中,依次连接各小长方形上端的中点,得到频率分布折线图.知识探究3频率分布折线图当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线.总体密度曲线知识探究4茎叶图 某赛季甲、乙两名运动员每场比赛得分的原始记录如下:甲运动员得分:
13,51,23, 8,26,38,16,33,14,28,39乙运动员得分:
49,24,12,31,50,31,44,36,15,37,25,36,3983643688391
2 5
4 5
1 1 6 7 6 9
9 4
0 变式1 下表给出了某校500名11岁男孩中用随机抽样得出的120人的身高(单位:cm):
(1)完成样本频率分布表(频率保留小数点后两位数字);
(2)请同学们画出频率分布直方图;
(3)估计身高小于134cm的男孩数占总男孩数的百分比. 变式精练解 (1)样本频率分布表如下(请同学们口答): 0.18 0.07 0.08 0.04 0.17 0.09 1.00 0.045 0.0175 0.02 0.01 0.07 0.0425 0.0125 0.0225 0.04 0.01 0.28 0.05 (2)频率分布直方图(请同学们作图):身高/cm0.07
0.06
0.05
0.04
0.03
0.02
0.01122 126 130 134 138 142 146 150 154 158O(3)估计身高小于134cm的男孩数占总男孩数的百分比.频率/组距 由频率分布直方图可知,身高小于134cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134cm的男孩数占总男孩数的19%.0.040.070.08快问快答1.有一个容量为200的样本,其频率分布直方图如右图所示.根据样本频率分布直方图,试估计:样本数据落在区间[10,12)内的频数为( )(A)18 (B)36
(C)54 (D)722.为比较A、B两种治疗失眠症的药的疗
效,随机选取20位患者服用A药,另20位患者服用B药,这40位患者在服药一段时间后,记录他们日均增加的睡眠时间(单位:h)如下茎叶图.从茎叶图看, 药的疗效更好.牛刀小试课堂小结掌握?体验?感受?1、频率分布表;
2、频率分布直方图;
3、频率分布折线图,茎叶图.1、列表作图的过程;
2、用样本的频率分布估计总体分布的方法;
3、数形结合思想.1、数学源于生活,用于生活;
2、统计知识的意义;
3、遇事理性对待.个人作业:
必做 课本P61练习 T1⑴
选做 课本P61练习 T2思考探究:课本P62课后作业敬请评委指正!
用样本的频率分布估计总体分布情境引入情境引入探究:如果标准太低,会影响居民的日常生活;如果标准太高,则不利于节水.
1、如果政府希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理?
2、你认为,为了较合理地确定出这个标准,需要做哪些工作? 我市政府为了节约生活用水,计划在本市试行居民生活用水定额管理:即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费.从这些数字中,我们能得到什么信息? 整理数据的两种基本方法:
用紧凑的表格改变数据的排列方式
用图将它们画出来通过抽样调查,获得了我市100户居民某年的月均用水量如下表(单位:t): 初中曾学过频数分布表和频数分布直方图. 下面将学习频率分布表和频率分布直方图,它们是从各小组数据在样本容量中所占比例大小的角度,来表示数据分布的规律. 频率:知识探究1频率分布表第一步:求极差
数据中最大值与最小值的差.思考1:上述100个样本数据的变化范围是什么?4.3-0.2=4.1思考2:分成多少组合适呢?第二步:决定组距与组数 组距:每个小组两端点的距离;
组数:组数k=极差/组距
当数据在100个以内时, 按数据多少,常分5—12组;
若k不是整数,则组数=[k]+1.4.1÷0.5=8.2,故可取组数为9按组距为0.5进行分组,上述数据据共分为几组?第四步:列频率分布表
计算各小组的频率,列出下面的频率分布表.第三步:将数据分组[0,0.5),[0.5,1),[1,1.5),[1.5,2),
[2,2.5),[2.5,3),[3,3.5),[3.5,4),
[4,4.5]思考3:
如何设定各组数据的范围呢?各组均为左闭右开区间,
最后一组是闭区间思考4:
你能将这些数据用表格反映出来吗? 频率分布表一般分5列:
1、“分组”
2、“频数累计”(可省)
3、“频数”
4、“频率”
5、“频率/组距”列频率分布表:频数的合计为样本容量频率合计为148152225146420.040.080.150.220.250.140.060.041001.000.020.080.160.300.440.500.280.120.080.04为直观反映样本数据在各组中的分布情况,我们将上述频率分布表中的有关信息用下面的频率分布直方图表示: 月均用水量/t0.050.100.20频率/组距第一步:画平面直角坐标系. 第二步:在横轴上均匀标出各组分点,在纵轴上标出单位长度.第三步:以组距为宽,各组的频率/组距为高,分别画出各组对应的小长方形y轴:频率/组距知识探究2频率分布直方图0.40011.52.53.52340.54.50.150.250.300.350.450.500.080.160.300.440.500.280.120.080.041、各组频率在图中怎么显示出来?长方形的面积=3、你能根据上述频率分布直方图,指出样本居民月均用水量的一些数据特点吗?2、各小长方体面积之和是否为定值? 各小长方形的面积之和为1.思考6:同一组数据,若组距不同,得到的条形图会不会相同?思考5:如果市政府希望85%以上的居民月用水量不超过标准,根据上述频率分布直方图,你对制定居民月用水量标准(即a的取值)有何建议? 在频率分布直方图中,依次连接各小长方形上端的中点,得到频率分布折线图.知识探究3频率分布折线图当样本容量无限增大,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线.总体密度曲线知识探究4茎叶图 某赛季甲、乙两名运动员每场比赛得分的原始记录如下:甲运动员得分:
13,51,23, 8,26,38,16,33,14,28,39乙运动员得分:
49,24,12,31,50,31,44,36,15,37,25,36,3983643688391
2 5
4 5
1 1 6 7 6 9
9 4
0 变式1 下表给出了某校500名11岁男孩中用随机抽样得出的120人的身高(单位:cm):
(1)完成样本频率分布表(频率保留小数点后两位数字);
(2)请同学们画出频率分布直方图;
(3)估计身高小于134cm的男孩数占总男孩数的百分比. 变式精练解 (1)样本频率分布表如下(请同学们口答): 0.18 0.07 0.08 0.04 0.17 0.09 1.00 0.045 0.0175 0.02 0.01 0.07 0.0425 0.0125 0.0225 0.04 0.01 0.28 0.05 (2)频率分布直方图(请同学们作图):身高/cm0.07
0.06
0.05
0.04
0.03
0.02
0.01122 126 130 134 138 142 146 150 154 158O(3)估计身高小于134cm的男孩数占总男孩数的百分比.频率/组距 由频率分布直方图可知,身高小于134cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134cm的男孩数占总男孩数的19%.0.040.070.08快问快答1.有一个容量为200的样本,其频率分布直方图如右图所示.根据样本频率分布直方图,试估计:样本数据落在区间[10,12)内的频数为( )(A)18 (B)36
(C)54 (D)722.为比较A、B两种治疗失眠症的药的疗
效,随机选取20位患者服用A药,另20位患者服用B药,这40位患者在服药一段时间后,记录他们日均增加的睡眠时间(单位:h)如下茎叶图.从茎叶图看, 药的疗效更好.牛刀小试课堂小结掌握?体验?感受?1、频率分布表;
2、频率分布直方图;
3、频率分布折线图,茎叶图.1、列表作图的过程;
2、用样本的频率分布估计总体分布的方法;
3、数形结合思想.1、数学源于生活,用于生活;
2、统计知识的意义;
3、遇事理性对待.个人作业:
必做 课本P61练习 T1⑴
选做 课本P61练习 T2思考探究:课本P62课后作业敬请评委指正!
