2.3.2 两个变量的线性相关 课件(15张PPT)
文档属性
| 名称 | 2.3.2 两个变量的线性相关 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 463.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 00:00:00 | ||
图片预览





文档简介
课件15张PPT。第二章 统 计 2.3 变量间的相关关系
2.3.2 两个变量的线性相关
人教A版 《数学》必修③【小阅读】:“回归”这个词是由英国著名的统计学家Francils Galton提出.1889年,他在研究祖先与后代身高之间的关系时发现,身材较高的父母,他们的孩子也较高,但这些孩子的平均身高并没有他们父母的平均身高高;身材较矮的父母,他们的孩子也较矮,但这些孩子的平均身高却比他们父母的平均身高高.
Galton把这种后代的身高向中间值靠近的趋势称为“回归现象”.
后来人们把由一个变量的变化去推测另一个变量的变化的方法称为回归方法.(一)、课题引入 【引例】:(2011年广东高考)
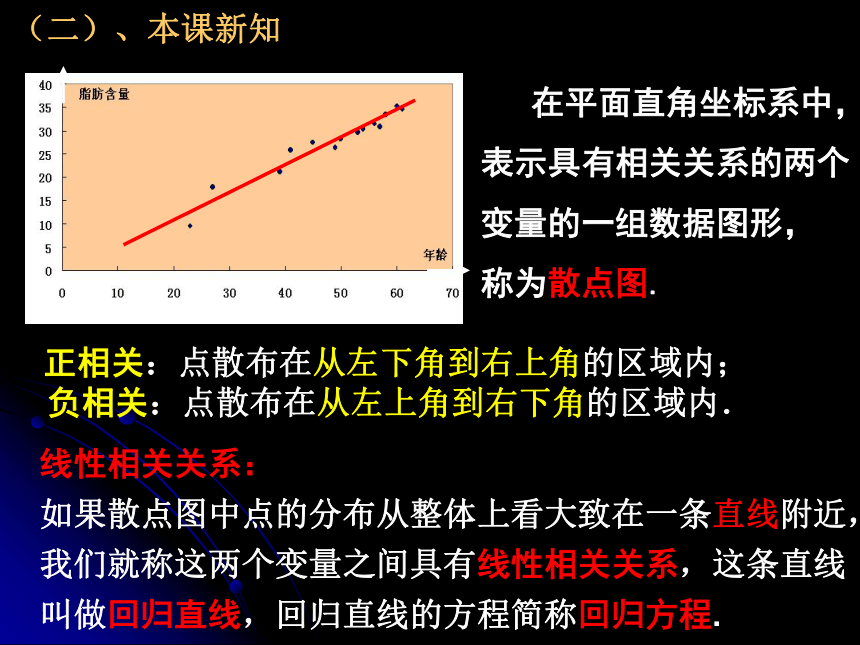
某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为_____cm.探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:(二)、本课新知 根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?(二)、本课新知 在平面直角坐标系中,
表示具有相关关系的两个
变量的一组数据图形,
称为散点图. 正相关:点散布在从左下角到右上角的区域内;
负相关:点散布在从左上角到右下角的区域内. 线性相关关系:
如果散点图中点的分布从整体上看大致在一条直线附近,
我们就称这两个变量之间具有线性相关关系,这条直线
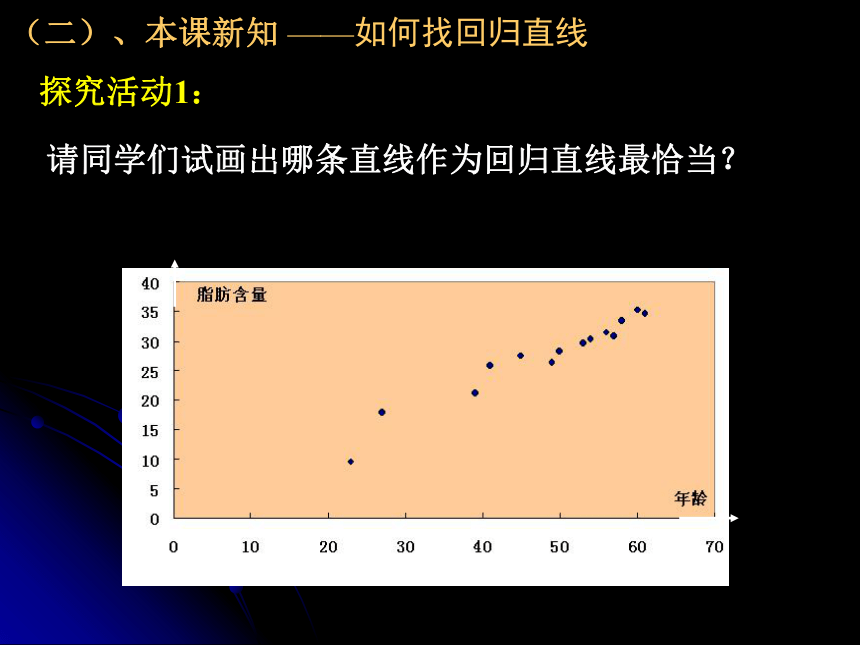
叫做回归直线,回归直线的方程简称回归方程.(二)、本课新知 ——如何找回归直线请同学们试画出哪条直线作为回归直线最恰当?探究活动1:(二)、本课新知 ——如何找回归直线方案一、在图中选取两点画直线,使得直线两侧的点的个数基本相同。采用测量的方法:(二)、本课新知 ——如何找回归直线方案二、在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。散点图(二)、本课新知 ——如何找回归直线方案三:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。【问题】如何用数学的方法来刻画“从整体上看,各点
与此直线的距离最小”? (二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——最小二乘法公式的探索过程根据数学理论含绝对值,
运算不方便(二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——应用公式,深化理解探究活动2:人体的脂肪百分比和年龄活动2:求出回归直线方程.思考:(1)试预测某人37岁时,体内的脂肪含量。
并说明结果的含义。
(2)由回归方程计算各个年龄的人体内脂肪
含量与真实值之间的关系 ?(三)、线性回归分析思想在实际中的应用 例、某数学老师身高176cm,他爷爷、父亲和儿子
的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为多少?解:根据题意,可知父亲与儿子的对应数据可列表如下:(四)、课堂小结
2.3.2 两个变量的线性相关
人教A版 《数学》必修③【小阅读】:“回归”这个词是由英国著名的统计学家Francils Galton提出.1889年,他在研究祖先与后代身高之间的关系时发现,身材较高的父母,他们的孩子也较高,但这些孩子的平均身高并没有他们父母的平均身高高;身材较矮的父母,他们的孩子也较矮,但这些孩子的平均身高却比他们父母的平均身高高.
Galton把这种后代的身高向中间值靠近的趋势称为“回归现象”.
后来人们把由一个变量的变化去推测另一个变量的变化的方法称为回归方法.(一)、课题引入 【引例】:(2011年广东高考)
某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为_____cm.探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:(二)、本课新知 根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?(二)、本课新知 在平面直角坐标系中,
表示具有相关关系的两个
变量的一组数据图形,
称为散点图. 正相关:点散布在从左下角到右上角的区域内;
负相关:点散布在从左上角到右下角的区域内. 线性相关关系:
如果散点图中点的分布从整体上看大致在一条直线附近,
我们就称这两个变量之间具有线性相关关系,这条直线
叫做回归直线,回归直线的方程简称回归方程.(二)、本课新知 ——如何找回归直线请同学们试画出哪条直线作为回归直线最恰当?探究活动1:(二)、本课新知 ——如何找回归直线方案一、在图中选取两点画直线,使得直线两侧的点的个数基本相同。采用测量的方法:(二)、本课新知 ——如何找回归直线方案二、在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。散点图(二)、本课新知 ——如何找回归直线方案三:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。【问题】如何用数学的方法来刻画“从整体上看,各点
与此直线的距离最小”? (二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——最小二乘法公式的探索过程根据数学理论含绝对值,
运算不方便(二)、本课新知 ——最小二乘法求回归方程系数(二)、本课新知 ——应用公式,深化理解探究活动2:人体的脂肪百分比和年龄活动2:求出回归直线方程.思考:(1)试预测某人37岁时,体内的脂肪含量。
并说明结果的含义。
(2)由回归方程计算各个年龄的人体内脂肪
含量与真实值之间的关系 ?(三)、线性回归分析思想在实际中的应用 例、某数学老师身高176cm,他爷爷、父亲和儿子
的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为多少?解:根据题意,可知父亲与儿子的对应数据可列表如下:(四)、课堂小结
