3.3.1 几何概型 课件(23张PPT)
文档属性
| 名称 | 3.3.1 几何概型 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 564.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:00:34 | ||
图片预览







文档简介
课件23张PPT。几何概型回顾复习
1、古典概型的特征:
(1)试验中所有可能出现的基本事件只有有限个;
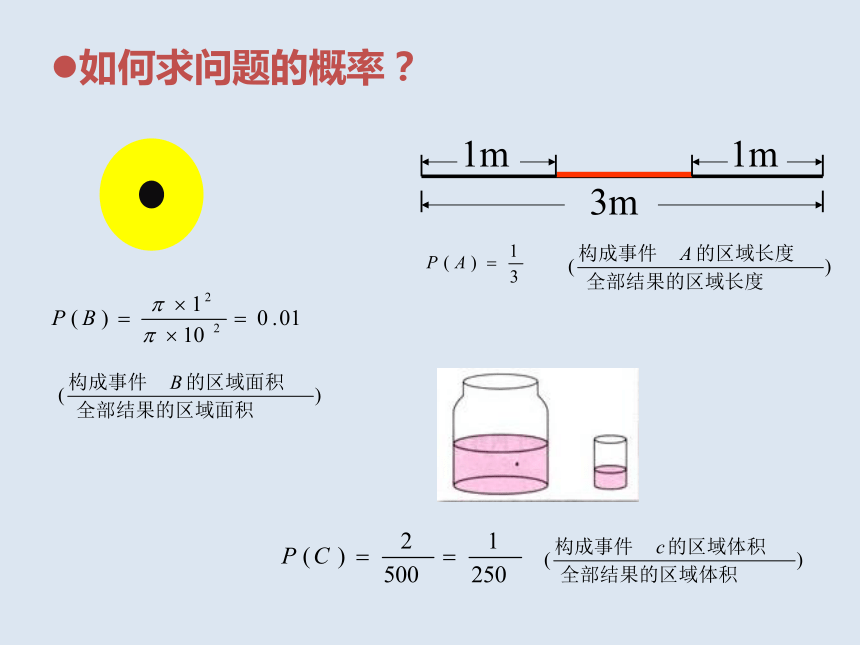
(2)每个基本事件出现的可能性相等2、公式 (1)试验中的基本事件是什么? (2)每个基本事件的发生是等可能的吗? (3)符合古典概型的特点吗?如何求其概率? 试验1:取1根长为3m的绳子,拉直后在任意位置断,那么剪得的两段长都不小于1m的概率有多大?
探究活动设:事件A:剪得的两段长都不小于1m.(1)试验中的基本事件是什么?(2)每个基本事件的发生是等可能的吗? (3)符合古典概型的特点吗?如何求其概率?探究活动试验2:下面是运动会射箭比赛的靶面,靶面半径为10cm,黑心半径为1cm,现一人随机射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,请问射中黑心的概率是多少?设:事件B:射中黑心.(1)试验中的基本事件是什么? (2)每个基本事件的发生是等可能的吗?(3)符合古典概型的特点吗?如何求其概率? 试验3:在500ml的水中有一个草履虫,现从中随机取出2ml水样放到显微镜下观察,则发现草履虫的概率是多少?探究活动设:事件c:2ml水样中发现草履虫. (1)一次试验可能出现的基本事件有无限多个;
(2) 每个基本事件的发生都具有等可能性. 上面三个随机试验有什么共同特点?如何求问题的概率?几何概型定义
在几何概型中,事件A的概率的计算公式:
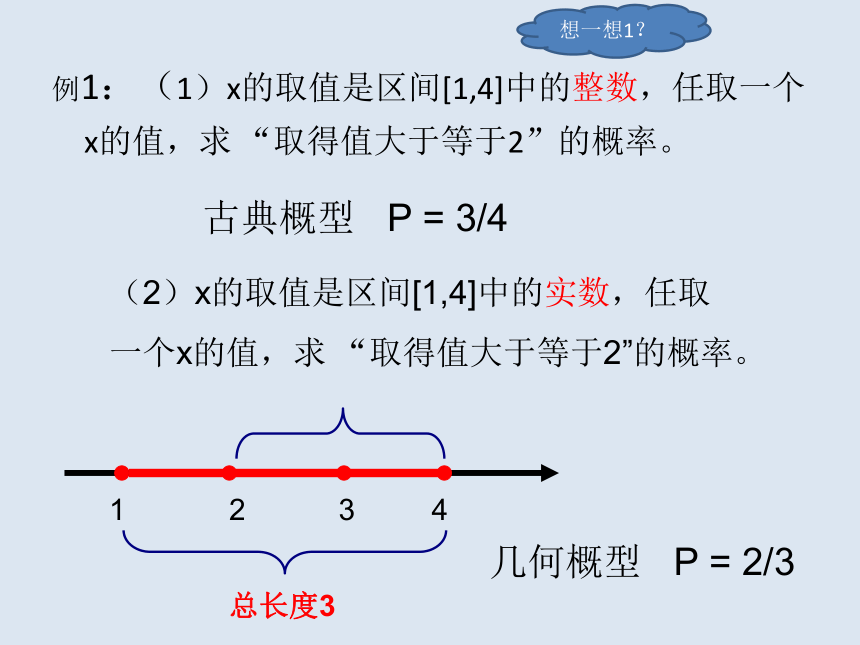
如果每个事件发生的概率只与构成该区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型.例1:(1)x的取值是区间[1,4]中的整数,任取一个x的值,求 “取得值大于等于2”的概率。古典概型 P = 3/4(2)x的取值是区间[1,4]中的实数,任取
一个x的值,求 “取得值大于等于2”的概率。123几何概型 P = 2/34总长度3想一想1?几何概型的解题步骤: 找出基本事件;
求出实验的全部结果所构成区域的几何度量;
求出构成事件A区域的几何度量;
利用公式
例2:(1)x和y取值都是区间[1,4]中的整数,任取一个x的值和一个y的值,求 的概率.
(2)x和y取值都是区间[1,4]中的实数,任取一个x的值和一个y的值,求 的概率.
想一想2?(1)x和y取值都是区间[1,4]中的整数,
任取一个x的值和一个y的值,
求 “ x – y ≥1 ”的概率。1 2 3 4 x1234y古典概型-1P=3/8(2)x和y取值都是区间[1,4]中的实数,
任取一个x的值和一个y的值,
求 “ x – y ≥1 ”的概率。1 2 3 4 x1234y几何概型-1作直线 x - y=1P=2/9ABCDEF送报人可能在早上6:30—7:30之间把报纸送到你家你父亲离开家去工作的时间在早上7:00—8:00之间问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?【变式题】假设你家订了一份报纸 6:30—7:30之间 报纸送到你家
7:00—8:00之间 父亲离开家
问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?提示:
如果用X表示报纸送到时间
用Y表示父亲离家时间
那么X与Y之间要满足哪些关系呢?难点突破:1.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率.解: 在AB上截取AC’=AC, 故AM<AC的概率等于
AM<AC’的概率.记事件A为“AM小于AC”,思考在单位圆内有一点A,现在随机的向圆内扔一颗小豆子.
(1)求小豆子落点正好为点A的概率.
(2)求小豆子落点正好不为点A的概率.
结论1:概率为0的事件不一定是不可能事件.结论2:概率为1的事件不一定是必然事件.课堂小结1.注意理解几何概型与古典概型的区别。
2.几何概型适用于是无穷多且事件是等可能发生的概率类型。
3.几何概型主要用于解决长度、面积、体积等有关的题目。
课后作业作业: 必做:142页 A组1、2题
选做:140页练习1
谢谢大家!
1、古典概型的特征:
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件出现的可能性相等2、公式 (1)试验中的基本事件是什么? (2)每个基本事件的发生是等可能的吗? (3)符合古典概型的特点吗?如何求其概率? 试验1:取1根长为3m的绳子,拉直后在任意位置断,那么剪得的两段长都不小于1m的概率有多大?
探究活动设:事件A:剪得的两段长都不小于1m.(1)试验中的基本事件是什么?(2)每个基本事件的发生是等可能的吗? (3)符合古典概型的特点吗?如何求其概率?探究活动试验2:下面是运动会射箭比赛的靶面,靶面半径为10cm,黑心半径为1cm,现一人随机射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,请问射中黑心的概率是多少?设:事件B:射中黑心.(1)试验中的基本事件是什么? (2)每个基本事件的发生是等可能的吗?(3)符合古典概型的特点吗?如何求其概率? 试验3:在500ml的水中有一个草履虫,现从中随机取出2ml水样放到显微镜下观察,则发现草履虫的概率是多少?探究活动设:事件c:2ml水样中发现草履虫. (1)一次试验可能出现的基本事件有无限多个;
(2) 每个基本事件的发生都具有等可能性. 上面三个随机试验有什么共同特点?如何求问题的概率?几何概型定义
在几何概型中,事件A的概率的计算公式:
如果每个事件发生的概率只与构成该区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型.例1:(1)x的取值是区间[1,4]中的整数,任取一个x的值,求 “取得值大于等于2”的概率。古典概型 P = 3/4(2)x的取值是区间[1,4]中的实数,任取
一个x的值,求 “取得值大于等于2”的概率。123几何概型 P = 2/34总长度3想一想1?几何概型的解题步骤: 找出基本事件;
求出实验的全部结果所构成区域的几何度量;
求出构成事件A区域的几何度量;
利用公式
例2:(1)x和y取值都是区间[1,4]中的整数,任取一个x的值和一个y的值,求 的概率.
(2)x和y取值都是区间[1,4]中的实数,任取一个x的值和一个y的值,求 的概率.
想一想2?(1)x和y取值都是区间[1,4]中的整数,
任取一个x的值和一个y的值,
求 “ x – y ≥1 ”的概率。1 2 3 4 x1234y古典概型-1P=3/8(2)x和y取值都是区间[1,4]中的实数,
任取一个x的值和一个y的值,
求 “ x – y ≥1 ”的概率。1 2 3 4 x1234y几何概型-1作直线 x - y=1P=2/9ABCDEF送报人可能在早上6:30—7:30之间把报纸送到你家你父亲离开家去工作的时间在早上7:00—8:00之间问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?【变式题】假设你家订了一份报纸 6:30—7:30之间 报纸送到你家
7:00—8:00之间 父亲离开家
问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?提示:
如果用X表示报纸送到时间
用Y表示父亲离家时间
那么X与Y之间要满足哪些关系呢?难点突破:1.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率.解: 在AB上截取AC’=AC, 故AM<AC的概率等于
AM<AC’的概率.记事件A为“AM小于AC”,思考在单位圆内有一点A,现在随机的向圆内扔一颗小豆子.
(1)求小豆子落点正好为点A的概率.
(2)求小豆子落点正好不为点A的概率.
结论1:概率为0的事件不一定是不可能事件.结论2:概率为1的事件不一定是必然事件.课堂小结1.注意理解几何概型与古典概型的区别。
2.几何概型适用于是无穷多且事件是等可能发生的概率类型。
3.几何概型主要用于解决长度、面积、体积等有关的题目。
课后作业作业: 必做:142页 A组1、2题
选做:140页练习1
谢谢大家!
