2.3 函数的单调性课件21张PPT

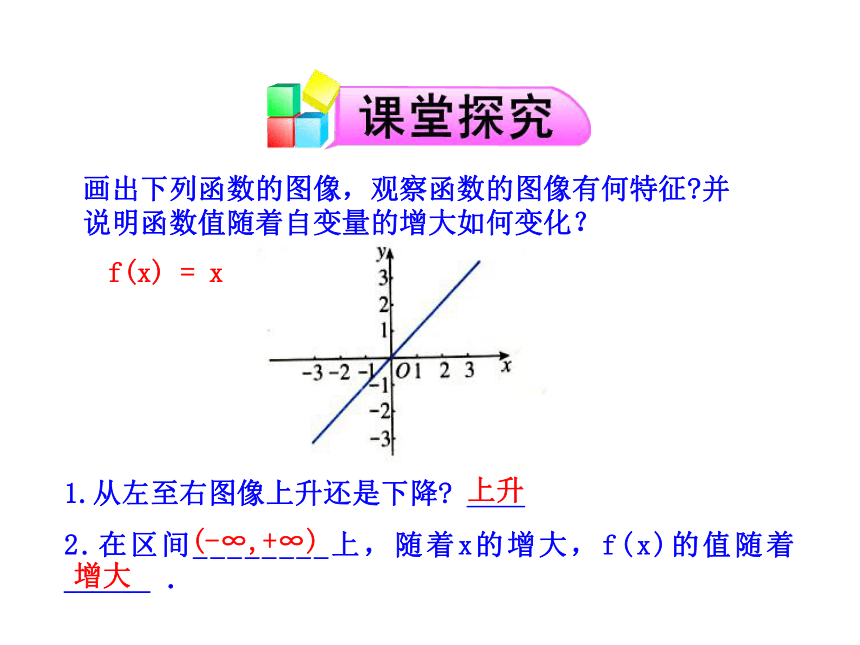
课件21张PPT。函数的单调性高一年级数学北师大版必修一 函数是描述变化规律的重要数学模型，建立函数的目的是研究函数值与自变量的关系，自变量的变化对函数值变化的影响是经常受到关注的问题．下面我们开始研究函数在这方面的一个主要性质——函数的单调性．§3 函数的单调性画出下列函数的图像，观察函数的图像有何特征?并说明函数值随着自变量的增大如何变化？ 1.从左至右图像上升还是下降? ____
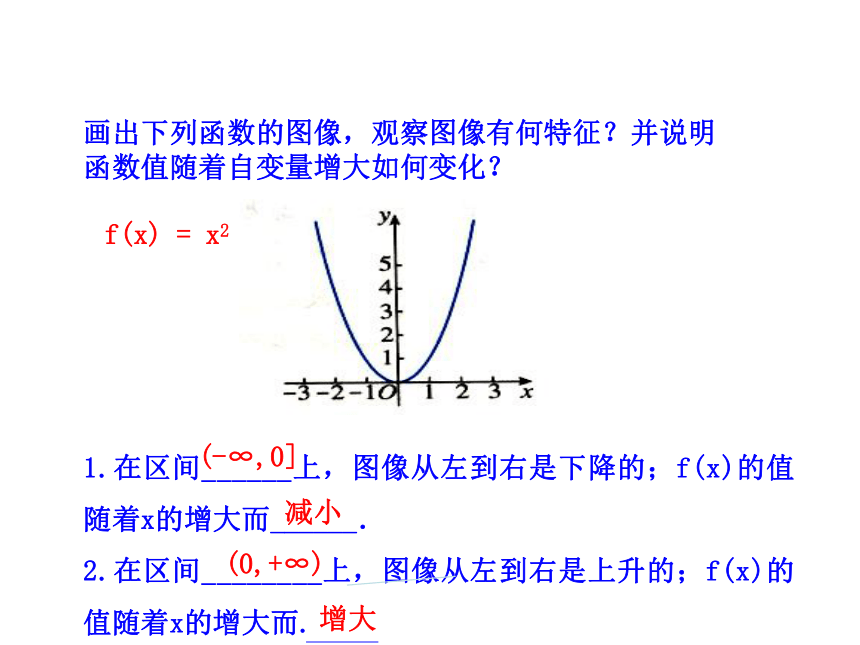
2.在区间________上，随着x的增大，f(x)的值随着 ______ ．f(x) = x(-∞,+∞)增大上升1.在区间______上，图像从左到右是下降的；f(x)的值随着x的增大而______．
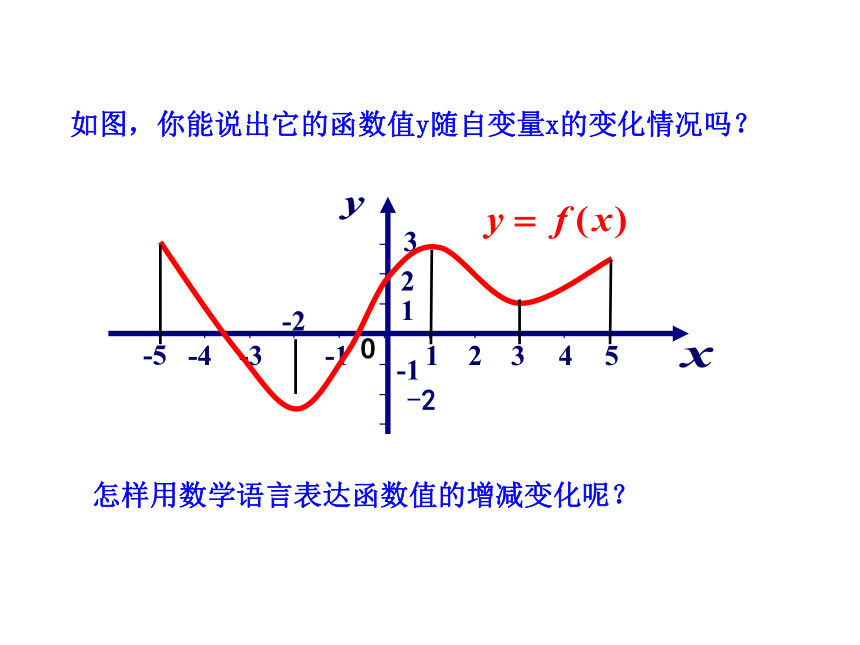
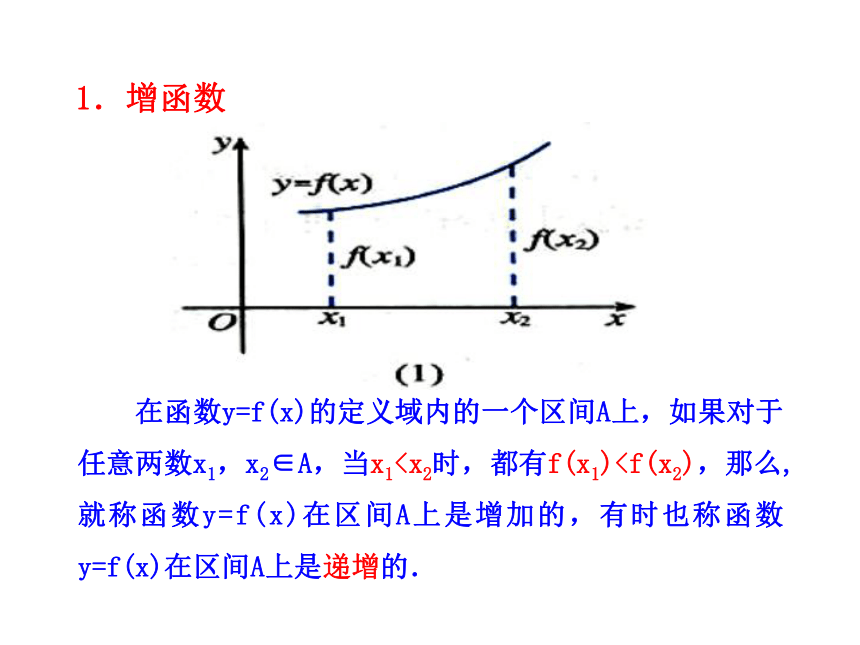
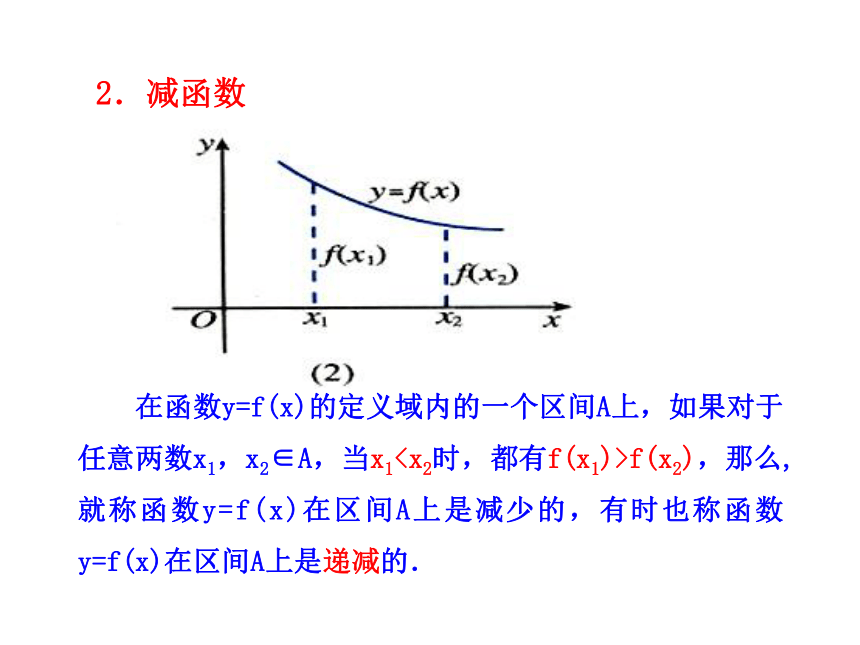
2.在区间________上，图像从左到右是上升的；f(x)的值随着x的增大而. f(x) = x2(-∞,0](0,+∞)减小画出下列函数的图像，观察图像有何特征？并说明函数值随着自变量增大如何变化？ 增大如图，你能说出它的函数值y随自变量x的变化情况吗？怎样用数学语言表达函数值的增减变化呢？O 在函数y=f(x)的定义域内的一个区间A上，如果对于任意两数x1，x2∈A，当x1f(x2)，那么,就称函数y=f(x)在区间A上是减少的，有时也称函数y=f(x)在区间A上是递减的． 3.单调区间、单调性、单调函数 如果y=f(x)在区间A上是增加的或是减少的，那么称A为单调区间.
如果函数y=f(x)在定义域的某个子集上是增加的或是减少的,那么就称函数y=f(x)在这个子集上具有单调性.
如果函数y=f(x)在整个定义域内是增加的或是减小的,我们分别称这个函数为增函数或减函数,统称为单调函数. 1.函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；注意： 2.必须是对于区间A内的任意两个自变量x1，x2；当x1f(x2)，分别是增函数或减函数.例1 画出函数 的图像，判断它的单调性，并加以证明.解：作出f(x)=3x+2的图像.由图看出，函数f(x)的图像在R上是上升的，函数f(x)是R上的增函数.证明：设 是R上的任意两个实数,且 则:在R上是增函数. 取值定序作差变形判断差值符号下结论 例2 说出函数 的单调区间，并指明在该区间上的单调性. 解:（-∞，0）和（0，+∞）都是函数的单调区间，在
这两个区间上函数 是减少的.图像不是连续上升或连续下降时，相同单调区间不能合并.证明: 设x1,x2是(0，+∞)上任意两个实数，且x10,又由
x10,
所以f(x1)- f(x2)>0, 即f(x1)> f(x2).变式练习变式练习 函数的单调性是对某个区间而言的，对于单独的一点，由于它的函数值是唯一确定的数，因而没有增减变化．因此，在考虑它的单调区间时，端点有定义时包括端点，端点无定义时不包括端点.1. (2012·东营高一检测）若函数f (x) 在区间[a, b]及(b, c]上都单调递减, 则f (x)在区间[a, c]上的单调性为( )A.单调递减;B.单调递增;C.一定不单调;D.不确定.D2.函数y=│x-2│的单调减区间是___________.（-∞，2）（1，+∞）3.函数 的单调增区间是_________. 4. 如图,已知y=f(x) 的图像(包括端点),根据图像说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.[-2,-1],[0,1]上是减函数;[-1,0],[1,2]上是增函数. ⒈讨论函数的单调性必须在定义域内进行,故讨论函数的单调性,必须先确定函数的定义域. ⒉根据定义证明函数单调性的一般步骤是：
⑴设 是给定区间内的任意两个值，且⑵作差 并将此差变形(要注意变形的程度).⑶判断 的正负（说理要充分）.⑷根据 的符号确定其增减性. 3.函数单调性的判断方法图像法和定义法。安徽省界首市第一中学2017年5月