4.1 对数及其运算课件22张PPT
文档属性
| 名称 | 4.1 对数及其运算课件22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 572.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 00:00:00 | ||
图片预览






文档简介
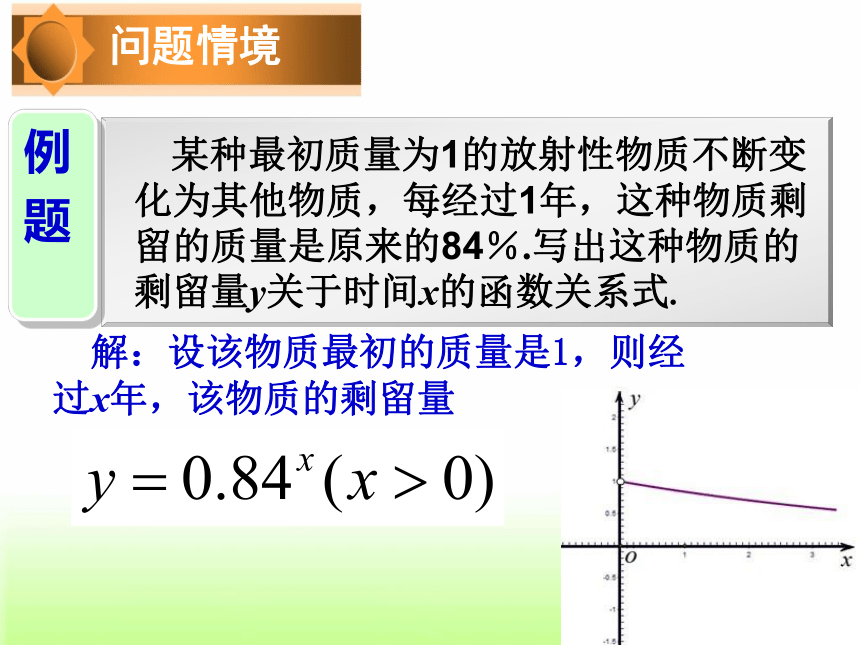
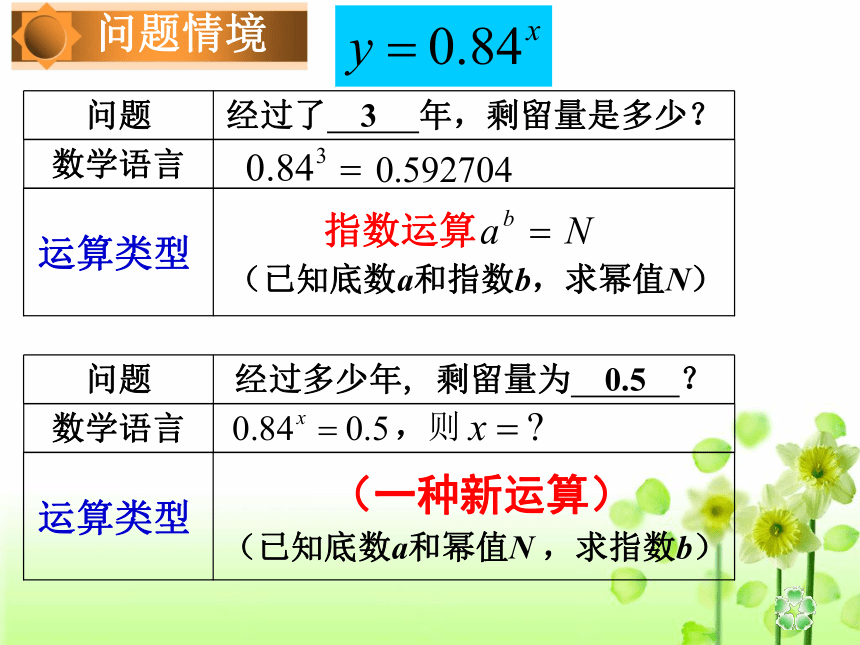
课件22张PPT。 我总是尽我的精力和才能来摆脱那种繁重而单调的计算. ——纳皮尔(苏格兰)生活因数学更美好,数学因生活更精彩! 解:设该物质最初的质量是1,则经过x年,该物质的剩留量 (已知底数a和指数b,求幂值N)(已知底数a和幂值N ,求指数b)(一种新运算)4.1 对 数教学目标: 1.理解对数的概念,能够熟练地进行对数式与指数式的互化。2.渗透应用意识,培养归纳思维能力和逻辑推理能力,提高数学发现能力。教学重点:
对数的概念。教学难点:
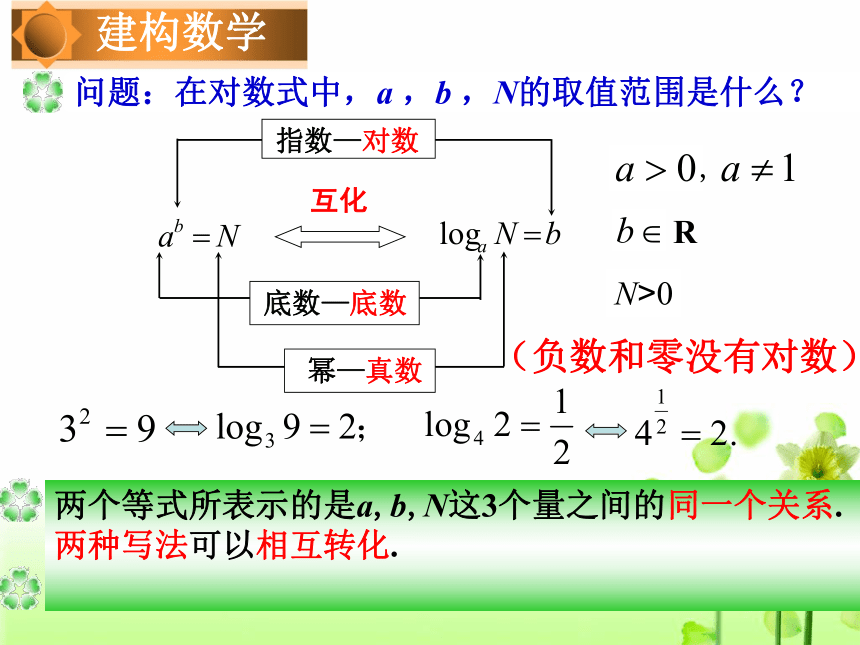
对数概念的理解。 一般地,如果a 的b次幂等于N,即
a b= N ,那么就称b是以a为底N的对数(logarithm),其中,a叫做对数的底数(base of logarithm),N叫做真数(proper number). 记作 ,读法写法错误写法互化 指数—对数 底数—底数 幂—真数(负数和零没有对数)活动一:学生写几个指数式,并分别改写成对数式,同桌判断读、写、转化是否正确;合作交流通常将以10为底的对数称为常用对数(common logarithm),等.如简记作为了方便起见,对数等.如,,常用对数与自然对数,根据对数的定义,写出下列各对数的值: 应用探究log31= (5) lg1= (6) lg10=(1)(4) (3) lne= (7) ln1=(4)(8)log0.50.5==0;=0;根据对数的定义,写出下列各对数的值: 应用探究=1;=1;=1; 观察上述各式,进行适当分类,归纳出一般性结论. log31 (5) lg1 (6) lg10(1)(4)■=0;■ (3) lne■ (7) ln1=0;(4)(8)=1.■log0.50.5=0=0 应用探究 log31 (5) lg1(1)(4)■=0■■ (7) ln1=0■=0;=0;写出下列各对数的值: 应用探究=1;=1;=1; 观察上述各式,进行适当分类,归纳一般性结论.
log31 (5) lg1 (6) lg10(1)(4)■■■=0;■ (3) lne■■ (7) ln1=0;(4)(4)(8)■=1.■log0.50.5 应用探究=1=1=1 (6) lg10■■ (3) lne■(8)■1log0.50.5=写出下列各对数的值: 应用探究=3=0.6 =-2=5 观察上述各式,进行适当分类,归纳一般性结论.(10)(12)(11)■■■■求下列各式的值:例1: 求下列各式的值:已知底数a和幂值N ,求指数b.对 数实例
引入转化与化归的思想互化性质四个结论特殊到一般;归纳猜想证明两个“宠儿” 18世纪的欧拉(Euler,1707~1783)深刻地
揭示了指数与对数的密切联系,他曾说“对数源于指数”. 恩格斯在他的著作《自然辨证法》中,曾经把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼茨的微积分共同称为17世纪的三大数学发明.法国著名的数学家、天文学家拉普拉斯(P.S.Laplace,1749 ~1827)曾说:对数可以缩短计算时间,“在实效上等于把天文学家的寿命延长了许多倍”. 对数是由苏格兰数学家纳皮尔(J.Napier,1550~1617)发明的,纳皮尔为了简化天文学问题的球面三角计算,在没有指数概念的情况下发明了对数,并于1614年在《论述对数的奇迹》中,介绍了他的方法和研究成果.实例
引入运算
性质函数
模型课本第87页
习题3—4 A组
1, 2, 3(1)(2)(3)(4), 4.
对数的概念。教学难点:
对数概念的理解。 一般地,如果a 的b次幂等于N,即
a b= N ,那么就称b是以a为底N的对数(logarithm),其中,a叫做对数的底数(base of logarithm),N叫做真数(proper number). 记作 ,读法写法错误写法互化 指数—对数 底数—底数 幂—真数(负数和零没有对数)活动一:学生写几个指数式,并分别改写成对数式,同桌判断读、写、转化是否正确;合作交流通常将以10为底的对数称为常用对数(common logarithm),等.如简记作为了方便起见,对数等.如,,常用对数与自然对数,根据对数的定义,写出下列各对数的值: 应用探究log31= (5) lg1= (6) lg10=(1)(4) (3) lne= (7) ln1=(4)(8)log0.50.5==0;=0;根据对数的定义,写出下列各对数的值: 应用探究=1;=1;=1; 观察上述各式,进行适当分类,归纳出一般性结论. log31 (5) lg1 (6) lg10(1)(4)■=0;■ (3) lne■ (7) ln1=0;(4)(8)=1.■log0.50.5=0=0 应用探究 log31 (5) lg1(1)(4)■=0■■ (7) ln1=0■=0;=0;写出下列各对数的值: 应用探究=1;=1;=1; 观察上述各式,进行适当分类,归纳一般性结论.
log31 (5) lg1 (6) lg10(1)(4)■■■=0;■ (3) lne■■ (7) ln1=0;(4)(4)(8)■=1.■log0.50.5 应用探究=1=1=1 (6) lg10■■ (3) lne■(8)■1log0.50.5=写出下列各对数的值: 应用探究=3=0.6 =-2=5 观察上述各式,进行适当分类,归纳一般性结论.(10)(12)(11)■■■■求下列各式的值:例1: 求下列各式的值:已知底数a和幂值N ,求指数b.对 数实例
引入转化与化归的思想互化性质四个结论特殊到一般;归纳猜想证明两个“宠儿” 18世纪的欧拉(Euler,1707~1783)深刻地
揭示了指数与对数的密切联系,他曾说“对数源于指数”. 恩格斯在他的著作《自然辨证法》中,曾经把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼茨的微积分共同称为17世纪的三大数学发明.法国著名的数学家、天文学家拉普拉斯(P.S.Laplace,1749 ~1827)曾说:对数可以缩短计算时间,“在实效上等于把天文学家的寿命延长了许多倍”. 对数是由苏格兰数学家纳皮尔(J.Napier,1550~1617)发明的,纳皮尔为了简化天文学问题的球面三角计算,在没有指数概念的情况下发明了对数,并于1614年在《论述对数的奇迹》中,介绍了他的方法和研究成果.实例
引入运算
性质函数
模型课本第87页
习题3—4 A组
1, 2, 3(1)(2)(3)(4), 4.
