1.1 利用函数性质判定方程解的存在 课件 20张PPT
文档属性
| 名称 | 1.1 利用函数性质判定方程解的存在 课件 20张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 650.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:09:24 | ||
图片预览






文档简介
课件20张PPT。1.1利用函数性质判定方程解的存在北师大版高中数学必修1 第四章 函数应用思考:下列方程有解吗?问题引入探究一:方程的解和相应函数有什么关系?
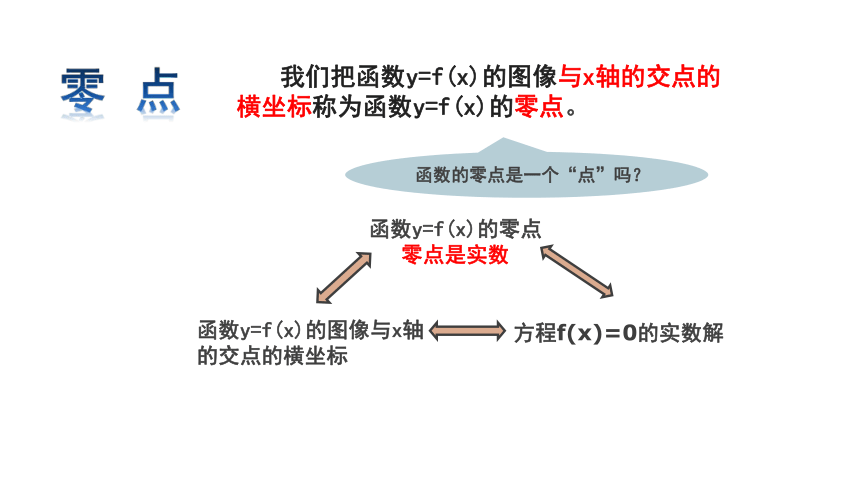
与新知探究利用函数性质判定方程解的存在 完成下列表格,思考一元二次方程的实数解与相应的二次函数图像与x轴的交点有什么关系?没有交点(1,0)x2-2x+3=0x2-2x+1=0(-1,0),(3,0)x2-2x-3=0没有实数解x1=x2=1x1=-1,x2=3y=x2-2x+3y=x2-2x+1y=x2-2x-3方程的实数解就是相应函数图像与x轴交点的横坐标。问 题:结 论: 我们把函数y=f(x)的图像与x轴的交点的横坐标称为函数y=f(x)的零点。 函数的零点是一个“点”吗?零 点方程f(x)=0的实数解函数y=f(x)的图像与x轴
的交点的横坐标函数y=f(x)的零点
零点是实数典
例
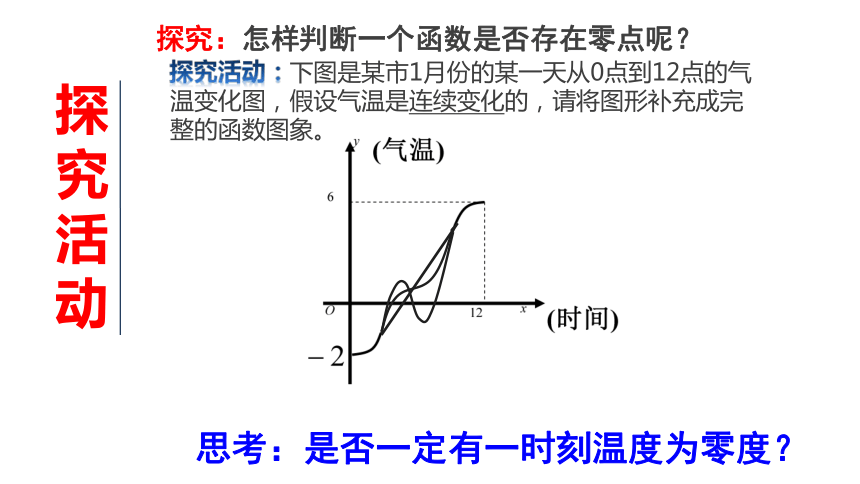
导悟探究活动:下图是某市1月份的某一天从0点到12点的气温变化图,假设气温是连续变化的,请将图形补充成完整的函数图象。思考:是否一定有一时刻温度为零度? 探究活动探究:怎样判断一个函数是否存在零点呢?
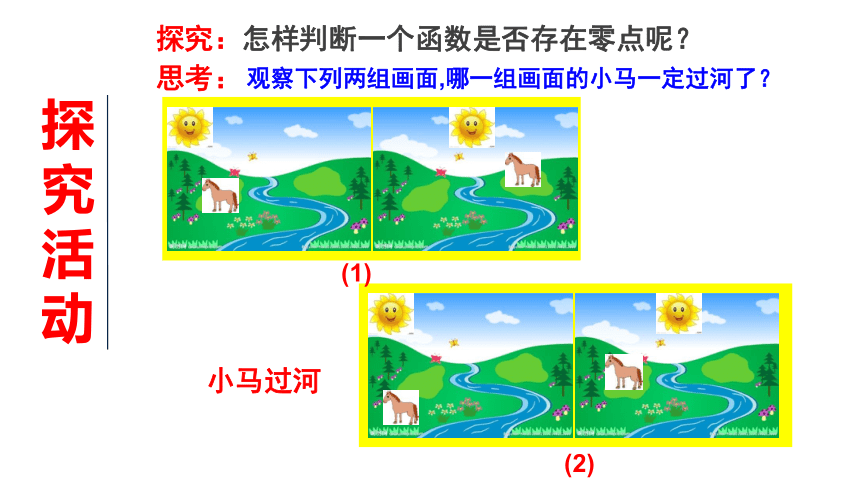
小马过河(2)(1)探究:怎样判断一个函数是否存在零点呢?思考:观察下列两组画面,哪一组画面的小马一定过河了? 探究活动 将河流抽象为x轴,将小马前后的两个位置抽象为函数y=f(x)图像上两点A和B。 f(a)·f(b)<0问题1: A、B两点与x轴满足怎样的关系时它们之间的函数图像与x轴一定会有交点?此时A、B两点的纵坐标满足什么条件呢?如f(x)= 图像如下:有f(-1) ·f(1)<0,但f(x)在(-1,1)没有零点,为什么?若只给条件f(a) · f(b)<0能否保证y=f(x)在(a,b)有零点,即函数图像与X轴有交点?问题2: 如果函数y=f(x)在区间[a,b]上的图像是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的解。函数零点存在性定理归纳总结利用函数性质判断方程在某个区间上有解的方法:对照函数零点存在性定理,每位同学先独立思考后再小组讨论下列几个问题:1 .正确使用定理,需满足什么条件?若不满足会如何?3 .若 f(a)·f(b)>0 ,则函数在区间(a,b)内一定没有零点吗? 如果函数y=f(x)在区间[a,b]上的图像是连续曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间 (a,b) 内至少有一个零点.讨 论:2.定理中的至少有一个是什么意思?4.给定理再加一个什么条件就能保证函数有唯一零点?4.如果函数 y=f(x) 在[a,b]上的图像是连续不断的一条曲线,f(a)f(b)﹤0,且在[a,b]上具有单调性,那么这个函数在(a,b)内必有唯一的一个零点。1.使用定理需满足 :(1)函数 y=f(x) 在[a,b]上的图像连续;(2)f(a)f(b)﹤0。
2.满足定理只能判断零点存在,不能判断有几个零点。3. 若f(a)f(b)>0,函数也可能有零点。定理解读探究:若函数y=f(x)在闭区间[a,b]上“连续不断”和“异号”中有一个或两个条件不成立,该函数是否还存在零点?拓展延伸①“不连续”“异号”③“不连续”“不异号”②“连续”“不异号”④“连续”“异号”①“不连续” “异号”②“连续” “不异号”③“不连续” “不异号”④“连续” “异号”结论:“连续”“异号”若不成立,则可能有也可能没有零点,但若“连续”“异号”都成立,则一定有零点!例2课堂练习AA知识:函数的零点的定义,
函数零点存在性定理及应用。 通过本节课的学习你学到了哪些数学
知识?又学到了哪些重要的数学思想?思想:转化与化归,函数与方程,
数形结合的思想。
课
堂
小
结课
后
作
业选做题:必做题:拓展题: 零点存在性定理中前面是闭区间[a,b],后面是
开区间(a,b),为什么?
与新知探究利用函数性质判定方程解的存在 完成下列表格,思考一元二次方程的实数解与相应的二次函数图像与x轴的交点有什么关系?没有交点(1,0)x2-2x+3=0x2-2x+1=0(-1,0),(3,0)x2-2x-3=0没有实数解x1=x2=1x1=-1,x2=3y=x2-2x+3y=x2-2x+1y=x2-2x-3方程的实数解就是相应函数图像与x轴交点的横坐标。问 题:结 论: 我们把函数y=f(x)的图像与x轴的交点的横坐标称为函数y=f(x)的零点。 函数的零点是一个“点”吗?零 点方程f(x)=0的实数解函数y=f(x)的图像与x轴
的交点的横坐标函数y=f(x)的零点
零点是实数典
例
导悟探究活动:下图是某市1月份的某一天从0点到12点的气温变化图,假设气温是连续变化的,请将图形补充成完整的函数图象。思考:是否一定有一时刻温度为零度? 探究活动探究:怎样判断一个函数是否存在零点呢?
小马过河(2)(1)探究:怎样判断一个函数是否存在零点呢?思考:观察下列两组画面,哪一组画面的小马一定过河了? 探究活动 将河流抽象为x轴,将小马前后的两个位置抽象为函数y=f(x)图像上两点A和B。 f(a)·f(b)<0问题1: A、B两点与x轴满足怎样的关系时它们之间的函数图像与x轴一定会有交点?此时A、B两点的纵坐标满足什么条件呢?如f(x)= 图像如下:有f(-1) ·f(1)<0,但f(x)在(-1,1)没有零点,为什么?若只给条件f(a) · f(b)<0能否保证y=f(x)在(a,b)有零点,即函数图像与X轴有交点?问题2: 如果函数y=f(x)在区间[a,b]上的图像是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的解。函数零点存在性定理归纳总结利用函数性质判断方程在某个区间上有解的方法:对照函数零点存在性定理,每位同学先独立思考后再小组讨论下列几个问题:1 .正确使用定理,需满足什么条件?若不满足会如何?3 .若 f(a)·f(b)>0 ,则函数在区间(a,b)内一定没有零点吗? 如果函数y=f(x)在区间[a,b]上的图像是连续曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间 (a,b) 内至少有一个零点.讨 论:2.定理中的至少有一个是什么意思?4.给定理再加一个什么条件就能保证函数有唯一零点?4.如果函数 y=f(x) 在[a,b]上的图像是连续不断的一条曲线,f(a)f(b)﹤0,且在[a,b]上具有单调性,那么这个函数在(a,b)内必有唯一的一个零点。1.使用定理需满足 :(1)函数 y=f(x) 在[a,b]上的图像连续;(2)f(a)f(b)﹤0。
2.满足定理只能判断零点存在,不能判断有几个零点。3. 若f(a)f(b)>0,函数也可能有零点。定理解读探究:若函数y=f(x)在闭区间[a,b]上“连续不断”和“异号”中有一个或两个条件不成立,该函数是否还存在零点?拓展延伸①“不连续”“异号”③“不连续”“不异号”②“连续”“不异号”④“连续”“异号”①“不连续” “异号”②“连续” “不异号”③“不连续” “不异号”④“连续” “异号”结论:“连续”“异号”若不成立,则可能有也可能没有零点,但若“连续”“异号”都成立,则一定有零点!例2课堂练习AA知识:函数的零点的定义,
函数零点存在性定理及应用。 通过本节课的学习你学到了哪些数学
知识?又学到了哪些重要的数学思想?思想:转化与化归,函数与方程,
数形结合的思想。
课
堂
小
结课
后
作
业选做题:必做题:拓展题: 零点存在性定理中前面是闭区间[a,b],后面是
开区间(a,b),为什么?
