3.3 指数函数的图像和性质 课件24张PPT
文档属性
| 名称 | 3.3 指数函数的图像和性质 课件24张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 847.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:13:35 | ||
图片预览






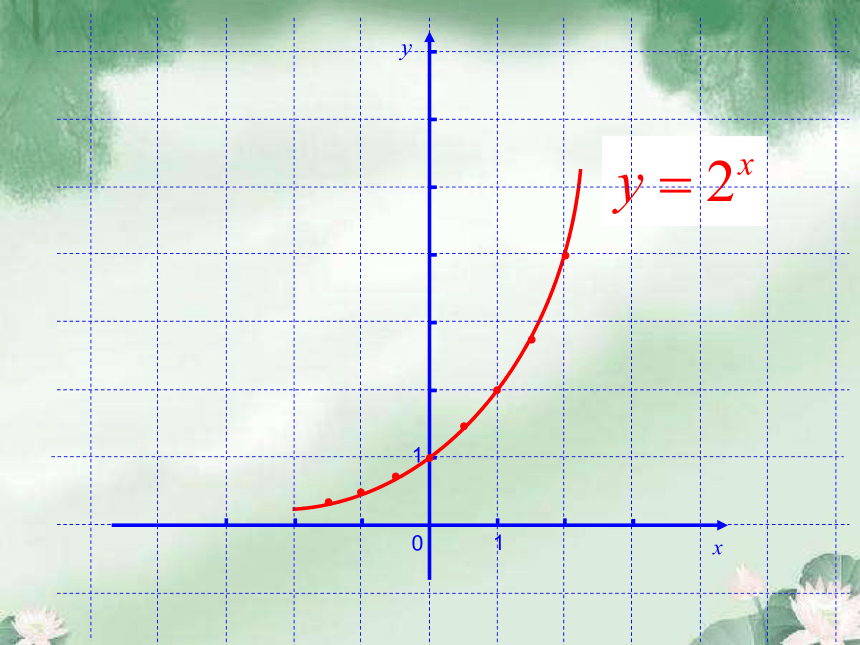
文档简介
课件24张PPT。指数函数的图象及性质
(第一课时) 一个细胞分裂x次,得到的细胞的个数y与x
的函数关系式是: .......实例1 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,… 《庄子·逍遥游》记载:一尺之椎,日取其
半,万世不竭.意思是一尺长的木棒,一天截取一
半,很长时间也截取不完.这样的一个木棒截取x
次,剩余长度y与x的关系是 . 实例2 一般地,函数____(a>0,且a≠1)叫做指数函
数,其中x是自变量,函数的定义域是__.y=axR指数函数的概念:探究一:思考:在指数函数y=ax中,为什么要规定a>0,且
a≠1呢?
提示:若a=0,
若a<0,比如y=(-4)x,这时对于x= (n∈N*)
在实数范围内函数值无意义.
若a=1,y=1x=1是一个常量,因此对它就没有研
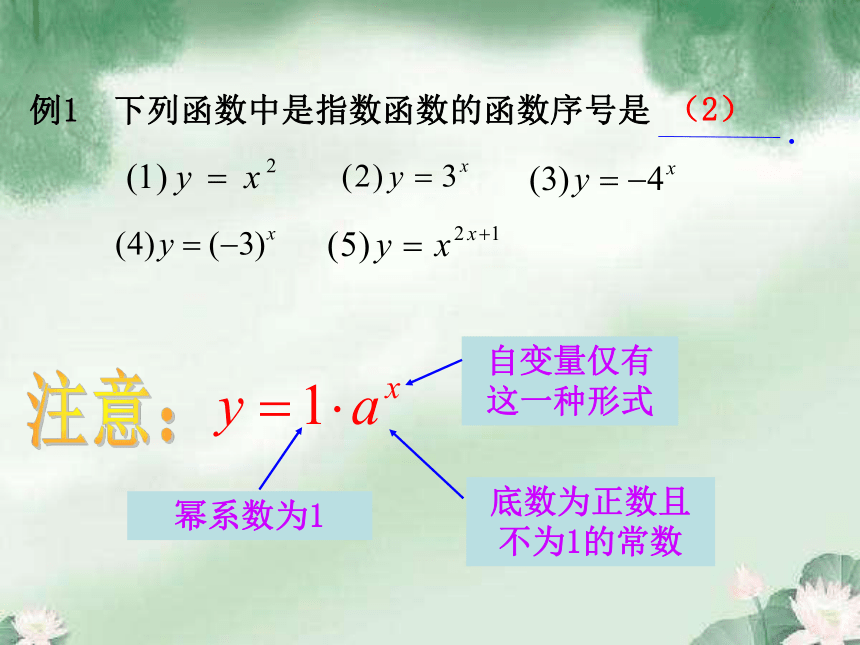
究的必要。为了避免上述各种情况,所以规定a>0且a≠1..(2)例1 下列函数中是指数函数的函数序号是幂系数为1底数为正数且不为1的常数自变量仅有这一种形式注意:例2 已知指数函数 f(x)=ax(a>0,且a≠1) 的图象经过点(3,π),求f(0) 的值.解析:指数函数的图象经过点(3,π),有f(3)=π,
即 a3=π, 解得
于是所以关键条件用 描点法 作出下列两组函数的图象,
然后写出其一些性质: 研究函数都会研究函数图象,如何画出指数函数的图象呢?描点法是作函数图象的通用方法哦探究二:011…0.0370.11
0.33
13927…
y=3-x…2793
10.330.110.037…
y=3x…321
0
-1
-2
-3
…
x(2) 与 的图象. 列表:同坐标系中画出两函数图象,并观察图象的特点关于y轴对称都过定点(1,0)关于y轴对称都过定点(1,0)y=ax (01)0101 图象共同特征:(1)图象可向左、右两方无限伸展(3)都经过坐标为(0,1)的点(2)图象都在x轴上方图象自左至右逐渐上升图象自左至右逐渐下降(2)在R上是减函数(1)过定点(0,1),即x=0时,y=1 性质(0,+∞) 值域R定义
域
图象a>101.70=1,
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1根据指数函数的性质不同底的要找中间值例4.已知 ,求数a的取值范围解析:由于 ,则 是减函数
所以 在第一象限当x取同一个数值时,函数值随底数的增大而增大
底数互为倒数,图象关于y轴对称 深入探究观察图象特征与底数关系: 如图,指数函数:A. y=ax B.y=bx C.y=cx D. y=dx
的图象,则a,b,c,d与1的大小关系是________________. b<a<1<d<c1如图,作直线x=1,与这4个函数图象分别交于E、F、G、H四点,由函数解析式易知E(1, c),
F(1,d),G(1, a),H(1,b),
由图象可直观看出c>d>1>a>b练习:1.若函数y=(a2-3a+3)ax是指数函数,则( )
A.a>1且a≠1 B.a=1
C.a=1或a=2 D.a=2
【解析】若函数y=(a2-3a+3)ax是指数函数,
则a2-3a+3=1,
解得a=2或a=1,
又因为指数函数的底数a>0且a≠1,
故a=2.D定义是考查的重点2.函数y=ax-3+2(a>0且a≠1)的图象一定经过点
P,则P点的坐标为( )
A.(-2,-3) B.(3,3)
C.(3,2) D.(-3,-2)
【解析】因为y=ax-3+2(a>0且a≠1),
所以当x-3=0,即x=3时,y=3,
所以函数y=ax-3+2(a>0且a≠1)的图象过定点
P(3,3).B 指数函数的图象和性质底数图象
定义域R值域性质(1)过定点(0,1),即x=0时,y=1(2)在R上是减函数 (2)在R上是增函数总结: 谢 谢!
(第一课时) 一个细胞分裂x次,得到的细胞的个数y与x
的函数关系式是: .......实例1 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,… 《庄子·逍遥游》记载:一尺之椎,日取其
半,万世不竭.意思是一尺长的木棒,一天截取一
半,很长时间也截取不完.这样的一个木棒截取x
次,剩余长度y与x的关系是 . 实例2 一般地,函数____(a>0,且a≠1)叫做指数函
数,其中x是自变量,函数的定义域是__.y=axR指数函数的概念:探究一:思考:在指数函数y=ax中,为什么要规定a>0,且
a≠1呢?
提示:若a=0,
若a<0,比如y=(-4)x,这时对于x= (n∈N*)
在实数范围内函数值无意义.
若a=1,y=1x=1是一个常量,因此对它就没有研
究的必要。为了避免上述各种情况,所以规定a>0且a≠1..(2)例1 下列函数中是指数函数的函数序号是幂系数为1底数为正数且不为1的常数自变量仅有这一种形式注意:例2 已知指数函数 f(x)=ax(a>0,且a≠1) 的图象经过点(3,π),求f(0) 的值.解析:指数函数的图象经过点(3,π),有f(3)=π,
即 a3=π, 解得
于是所以关键条件用 描点法 作出下列两组函数的图象,
然后写出其一些性质: 研究函数都会研究函数图象,如何画出指数函数的图象呢?描点法是作函数图象的通用方法哦探究二:011…0.0370.11
0.33
13927…
y=3-x…2793
10.330.110.037…
y=3x…321
0
-1
-2
-3
…
x(2) 与 的图象. 列表:同坐标系中画出两函数图象,并观察图象的特点关于y轴对称都过定点(1,0)关于y轴对称都过定点(1,0)y=ax (0
域
图象a>10
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1根据指数函数的性质不同底的要找中间值例4.已知 ,求数a的取值范围解析:由于 ,则 是减函数
所以 在第一象限当x取同一个数值时,函数值随底数的增大而增大
底数互为倒数,图象关于y轴对称 深入探究观察图象特征与底数关系: 如图,指数函数:A. y=ax B.y=bx C.y=cx D. y=dx
的图象,则a,b,c,d与1的大小关系是________________. b<a<1<d<c1如图,作直线x=1,与这4个函数图象分别交于E、F、G、H四点,由函数解析式易知E(1, c),
F(1,d),G(1, a),H(1,b),
由图象可直观看出c>d>1>a>b练习:1.若函数y=(a2-3a+3)ax是指数函数,则( )
A.a>1且a≠1 B.a=1
C.a=1或a=2 D.a=2
【解析】若函数y=(a2-3a+3)ax是指数函数,
则a2-3a+3=1,
解得a=2或a=1,
又因为指数函数的底数a>0且a≠1,
故a=2.D定义是考查的重点2.函数y=ax-3+2(a>0且a≠1)的图象一定经过点
P,则P点的坐标为( )
A.(-2,-3) B.(3,3)
C.(3,2) D.(-3,-2)
【解析】因为y=ax-3+2(a>0且a≠1),
所以当x-3=0,即x=3时,y=3,
所以函数y=ax-3+2(a>0且a≠1)的图象过定点
P(3,3).B 指数函数的图象和性质底数图象
定义域R值域性质(1)过定点(0,1),即x=0时,y=1(2)在R上是减函数 (2)在R上是增函数总结: 谢 谢!
