5.2 y=㏒?x的图像和性质

(共15张PPT)
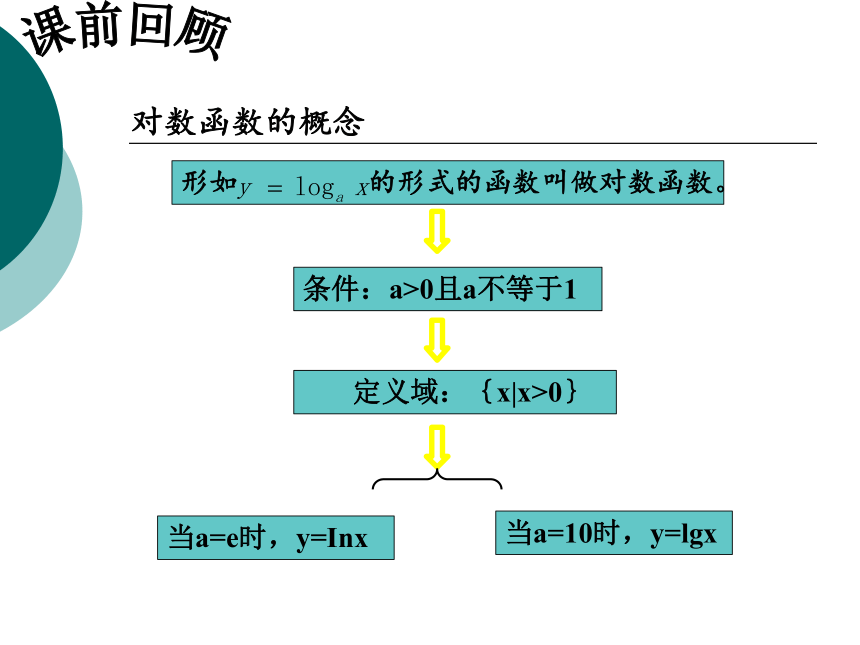
形如 的形式的函数叫做对数函数。
对数函数的概念
定义域：｛x|x>0｝
当a=10时，y=lgx
当a=e时，y=Inx
条件：a>0且a不等于1
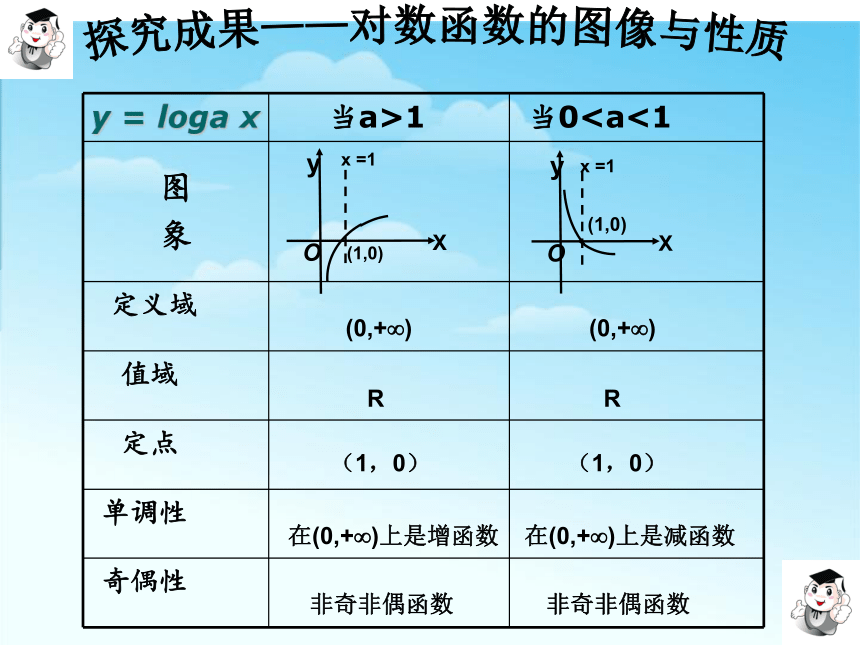
y = loga x (a＞0,且a≠ 1) 图象与性质
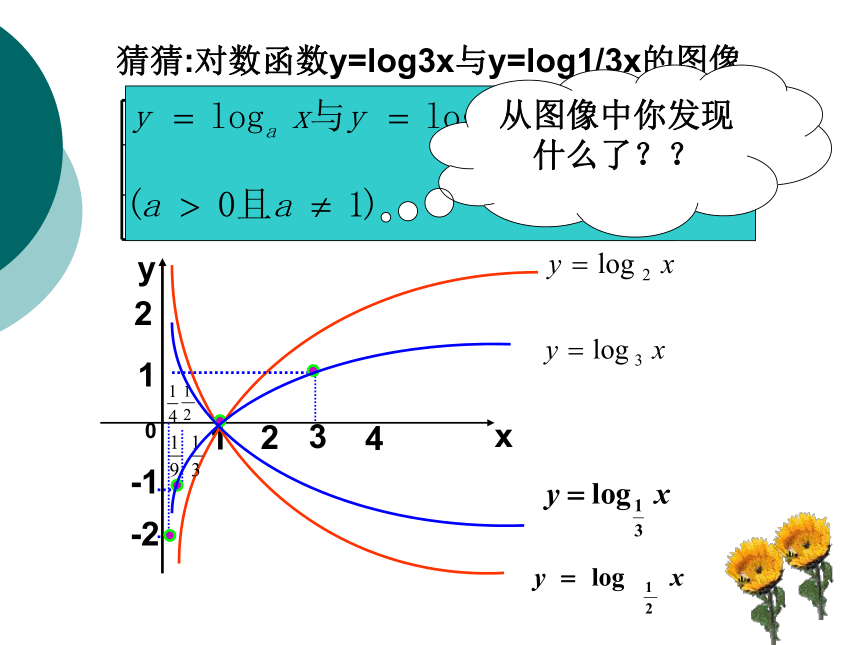
猜猜:对数函数y=log3x与y=log1/3x的图像
从图像中你发现什么了？？
x … 1/9 1/3 1 3 9 …
Y=log3x -2 -1 0 1 2
y=log1/3x 2 1 0 -1 -2
(0,+?)
(0,+?)
R
R
（1，0）
（1，0）
在(0,+?)上是增函数
在(0,+?)上是减函数
非奇非偶函数
非奇非偶函数
y = loga x 当a>1 当0图
象
定义域
值域
定点
单调性
奇偶性
解： ①要使函数有意义，则


∴函数的定义域是{x|x≠0}
例1：求下列函数的定义域：
①y=logax2 ②y=loga(4-x)
求解对数函数定义域问题的关键
真数大于零
当真数为某一代数式时，可将其看作一个整体单独提出来求其大于零的解集即该函数的定义域
练习：求下列函数定义域 y=loga(4-x)
y=log3(1/2x-1)
例2 比较下列各组数中两个值的大小：

⑴ log 23.4 , log 28.5
　　
⑵ log 0.31.8 , log 0.32.7
　　
⑶ log a5.1 , log a5.9 ( a＞0 , a≠1 )
比较两个同底对数值的大小时
首先观察底数a>1还是0且小于1时为减函数）；
再比较真数值的大小；
最后根据单调性得出结果。
分析
　
解:

⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
∴ log 23.4＜log 28.5
⑵∵对数函数 y = log 0.3 x
在(0,+∞)上是减函数

∴log 0.31.8＞log 0.32.7
且 3.4<8.5

且1.8<2.7
log a5.1＞log a5.9

当0＜a＜1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1＜log a5.9
（3）当a＞1时,函数y=log ax在(0,+∞)上是增函数,于是
你能口答吗？
变一变还能口答吗？
<
，则m___n;
则m___n.
>
<
>
练习：比较大小
① log76 1 ② log0.53 1
③ log67 1 ④ log0.60.1 1
⑤ log35.1 0 ⑥ log0.12 0
⑦ log20.8 0 ⑧ log0.20.6 0
<
<
<
>
>
>
<
>
※关键　　
引申思考——比较大小时底数不同怎么办？
(1） log35 log53
(2） log32 log20.8







?
?
　
当底数不同，真数也不同时
引入中间变量0或者1（各种变型）
探究对数函数的图像
总结对数函数的性质
利用对数函数的性质求定义域
利用对数函数的性质比较大小
思想方法：数形结合
观察图像的特征
作业：课本P97 第三题
第四题