3.3 模拟方法---概率的应用课件27张PPT
文档属性
| 名称 | 3.3 模拟方法---概率的应用课件27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-31 23:15:28 | ||
图片预览








文档简介
课件27张PPT。模拟方法--概率的应用情境导入情境导入 2016年11月18日,是“神舟十一号”回家的日子,它在内蒙古四子王旗着陆.假设着陆场为方圆200 km,而主着陆场为方圆120 km的圆形区域.飞船在着陆场内任何一个地方着陆的可能性相等.如何计算飞船在主着陆场内着陆的概率?情境导入1.正确理解几何概型的概念;用随机模拟的方法估计概率(重点)
2.掌握几何概型的概率求法;(难点)
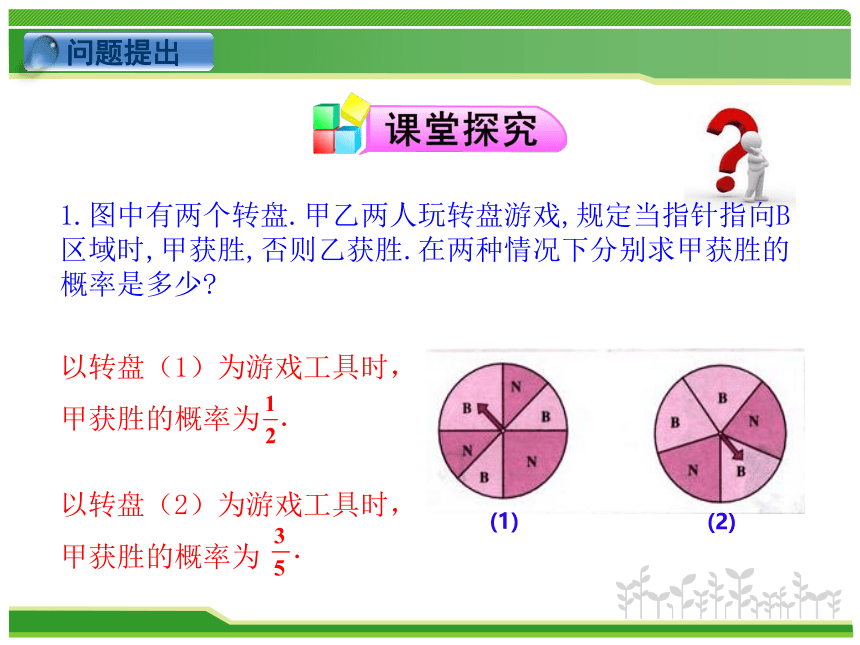
3.会根据古典概型与几何概型的区别与联系来判别某种概型是古典概型还是几何概型.(难点)1.图中有两个转盘.甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
以转盘(1)为游戏工具时,
甲获胜的概率为
以转盘(2)为游戏工具时,
甲获胜的概率为 事实上,甲获胜的概率与字母B所在扇形区域的圆弧的长度有关,而与字母B所在区域的位置无关.因为转转盘时,指针指向圆弧上哪一点都是等可能的.不管这些区域是相邻,还是不相邻,甲获胜的概率是不变的.2.下图是卧室和书房地板的示意图,图中所有方砖除颜
色外完全相同,甲壳虫 分别在卧室和书房中自由地 飞来飞去,并随意停留在某块方砖上,问在哪个房间里,
甲壳虫停留在黑砖上的概率大?
卧 室书 房 事实上,甲壳虫停留在黑砖上的概率与黑砖的总面积有关.3.用大小两个玻璃盆分别去捞鱼缸中红白相间的金鱼,哪个捞到金鱼的概率大?
事实上,捞到金鱼的概率与盆的体积有关.上面三个随机试验有什么共同特点? (1)一次试验的所有可能出现的结果有无限多个;
(2) 每个结果的发生的可能性大小相等. 如果每个基本事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,而与区域的形状、位置无关,则
称这样的概率模型为
几何概型.古典概型几何概型共同点 不同点基本事件个数的有限性基本事件发生的等可能性基本事件发生的等可能性基本事件个数的无限性问题:(1)x的取值是区间[1,4]中的整数,任取一个x的值,求 “取得值大于2”的概率。古典概型 P = 2/4=1/2(2)x的取值是区间[1,4]中的实数,任取一个x的值,求 “取得值大于2”的概率。123几何概型 P = 2/34总长度3例1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?例2.2016年11月18日,是“神舟十一号”回家的日子,它在内蒙古四子王旗着陆.假设着陆场为方圆200 km,而主着陆场为方圆120 km的区域.飞船在着陆场内任何一个地方着陆的可能性相等.飞船在主着陆场内着陆的概率是多少?例3 . 有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.合作探究例1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?解:记“剪得两段绳子都不小于10cm”
为事件A.用线段MN表示30cm的绳子,E、F为MN的两个三等分点.
∵EF= 10cm,∴P(A)=
例2. 求解“引入新课”中的问题。
解:设“飞船在主着陆场内着陆”为事件A,例3 . 有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.分析:细菌在这升水中的分布可以看作是随机的,取得0.1升水可作为事件的区域。解:取出0.1升中“含有这个细菌”这一事件记为A,则 实验:取一个正方形,在面积为四分之一的部分画上阴影,随机地向正方形中撒一把芝麻(以数100粒为例),假设每一粒芝麻落在正方形内的每一个位置的可能性相等.统计落在阴影内的芝麻数与落在矩形内的总芝麻数,观察它们有怎样的比例关系? 分析:由于区域A的面积是正方形面积的1/4,因此大约有1/4的芝麻(25个)落在阴影部分A内.下面我将通过计算机做模拟实验,来验证分析的结果是否正确.落在区域A内的芝麻数落在正方形内的芝麻数≈区域A的面积正方形的面积通过上述的试验,不难得出下面的结论: 一般地,在向几何区域D中随机地投一点,记事件A为“该点落在其内部一个区域d内”,则事件A发生的概率为:注:利用这个定理可以估算不规则图形的面积、体积。如何估算右图不规则图形的面积? 小明家的晚报在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐。你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大? 我们用模拟方法来估计晚报在晚餐开始之前被送到的概率:
用两个转盘来模拟上述过程,一个转盘用于模拟晚报的送达,另一个转盘用于模拟晚餐,两个转盘各转动一次并记录下结果就完成一次模拟。 2.在腰长为2的等腰直角三角形内任取一点,使得该点到三角形直角顶点的距离不大于1的概率为多少?3.在1升高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10毫升,含有麦锈病种子的概率是多少? π/81/1001.公共汽车每隔10分钟就有一辆汽车通过,乘客到达汽车站的任意时刻都是等可能的,则乘客候车时间不超过3分钟的概率为 .3/10课堂小结课堂小结1.数学知识:
2.数学思想方法:
类比、转化;模拟方法几何概型的特点:无限性、等可能性课堂小结谢谢大家作业:
1.习题3-3 1、2
2.用所学的几何概型知识来构建一个求圆周率的模拟方法.“意志”保护“愿望”,使“愿望”能够继续“愿望”下去而不冒巨大的危险。
2.掌握几何概型的概率求法;(难点)
3.会根据古典概型与几何概型的区别与联系来判别某种概型是古典概型还是几何概型.(难点)1.图中有两个转盘.甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
以转盘(1)为游戏工具时,
甲获胜的概率为
以转盘(2)为游戏工具时,
甲获胜的概率为 事实上,甲获胜的概率与字母B所在扇形区域的圆弧的长度有关,而与字母B所在区域的位置无关.因为转转盘时,指针指向圆弧上哪一点都是等可能的.不管这些区域是相邻,还是不相邻,甲获胜的概率是不变的.2.下图是卧室和书房地板的示意图,图中所有方砖除颜
色外完全相同,甲壳虫 分别在卧室和书房中自由地 飞来飞去,并随意停留在某块方砖上,问在哪个房间里,
甲壳虫停留在黑砖上的概率大?
卧 室书 房 事实上,甲壳虫停留在黑砖上的概率与黑砖的总面积有关.3.用大小两个玻璃盆分别去捞鱼缸中红白相间的金鱼,哪个捞到金鱼的概率大?
事实上,捞到金鱼的概率与盆的体积有关.上面三个随机试验有什么共同特点? (1)一次试验的所有可能出现的结果有无限多个;
(2) 每个结果的发生的可能性大小相等. 如果每个基本事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,而与区域的形状、位置无关,则
称这样的概率模型为
几何概型.古典概型几何概型共同点 不同点基本事件个数的有限性基本事件发生的等可能性基本事件发生的等可能性基本事件个数的无限性问题:(1)x的取值是区间[1,4]中的整数,任取一个x的值,求 “取得值大于2”的概率。古典概型 P = 2/4=1/2(2)x的取值是区间[1,4]中的实数,任取一个x的值,求 “取得值大于2”的概率。123几何概型 P = 2/34总长度3例1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?例2.2016年11月18日,是“神舟十一号”回家的日子,它在内蒙古四子王旗着陆.假设着陆场为方圆200 km,而主着陆场为方圆120 km的区域.飞船在着陆场内任何一个地方着陆的可能性相等.飞船在主着陆场内着陆的概率是多少?例3 . 有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.合作探究例1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?解:记“剪得两段绳子都不小于10cm”
为事件A.用线段MN表示30cm的绳子,E、F为MN的两个三等分点.
∵EF= 10cm,∴P(A)=
例2. 求解“引入新课”中的问题。
解:设“飞船在主着陆场内着陆”为事件A,例3 . 有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.分析:细菌在这升水中的分布可以看作是随机的,取得0.1升水可作为事件的区域。解:取出0.1升中“含有这个细菌”这一事件记为A,则 实验:取一个正方形,在面积为四分之一的部分画上阴影,随机地向正方形中撒一把芝麻(以数100粒为例),假设每一粒芝麻落在正方形内的每一个位置的可能性相等.统计落在阴影内的芝麻数与落在矩形内的总芝麻数,观察它们有怎样的比例关系? 分析:由于区域A的面积是正方形面积的1/4,因此大约有1/4的芝麻(25个)落在阴影部分A内.下面我将通过计算机做模拟实验,来验证分析的结果是否正确.落在区域A内的芝麻数落在正方形内的芝麻数≈区域A的面积正方形的面积通过上述的试验,不难得出下面的结论: 一般地,在向几何区域D中随机地投一点,记事件A为“该点落在其内部一个区域d内”,则事件A发生的概率为:注:利用这个定理可以估算不规则图形的面积、体积。如何估算右图不规则图形的面积? 小明家的晚报在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐。你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大? 我们用模拟方法来估计晚报在晚餐开始之前被送到的概率:
用两个转盘来模拟上述过程,一个转盘用于模拟晚报的送达,另一个转盘用于模拟晚餐,两个转盘各转动一次并记录下结果就完成一次模拟。 2.在腰长为2的等腰直角三角形内任取一点,使得该点到三角形直角顶点的距离不大于1的概率为多少?3.在1升高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10毫升,含有麦锈病种子的概率是多少? π/81/1001.公共汽车每隔10分钟就有一辆汽车通过,乘客到达汽车站的任意时刻都是等可能的,则乘客候车时间不超过3分钟的概率为 .3/10课堂小结课堂小结1.数学知识:
2.数学思想方法:
类比、转化;模拟方法几何概型的特点:无限性、等可能性课堂小结谢谢大家作业:
1.习题3-3 1、2
2.用所学的几何概型知识来构建一个求圆周率的模拟方法.“意志”保护“愿望”,使“愿望”能够继续“愿望”下去而不冒巨大的危险。
